树--09---2-3查找树

Posted 2021-10-22 高高for 循环

文章目录

• 二叉查找树弊端
• • • • ==效率低的原因在于这个树并不平衡==
• 查找树
• • 2-3查找树的定义
  • 2-结点：
  • 3-结点：
• 查找
• 插入
• • 1、 向2-结点中插入新键
  • 2、向一棵只含有一个3-结点的树中插入新键
  • 3、向一个父结点为2-结点的3-结点中插入新键
  • 4、向一个父结点为3-结点的3-结点中插入新键
  • 5、分解根结点
• 小结
• • • • 我们发现在插入的时候，2-3树需要做一些==局部的变换来保持2-3树的平衡==。
  • 一棵完全平衡的2-3树具有以下性质：
  • 2-3树的实现

---

二叉查找树弊端

之前我们学习过二叉查找树，发现它的查询效率比单纯的链表和数组的查询效率要高很多，大部分情况下，确实是这样的，但不幸的是，在最坏情况下，二叉查找树的性能还是很糟糕。

例如我们依次往二叉查找树中插入9,8,7,6,5,4,3,2,1这9个数据，那么最终构造出来的树是长得下面这个样子：
我们会发现，如果我们要查找1这个元素，查找的效率依旧会很低。效率低的原因在于这个树并不平衡，全部是向左边分支，

效率低的原因在于这个树并不平衡

如果我们有一种方法，能够不受插入数据的影响，让生成的树都像完全二叉树那样，那么即使在最坏情况下，查找的效率依旧会很好。

查找树

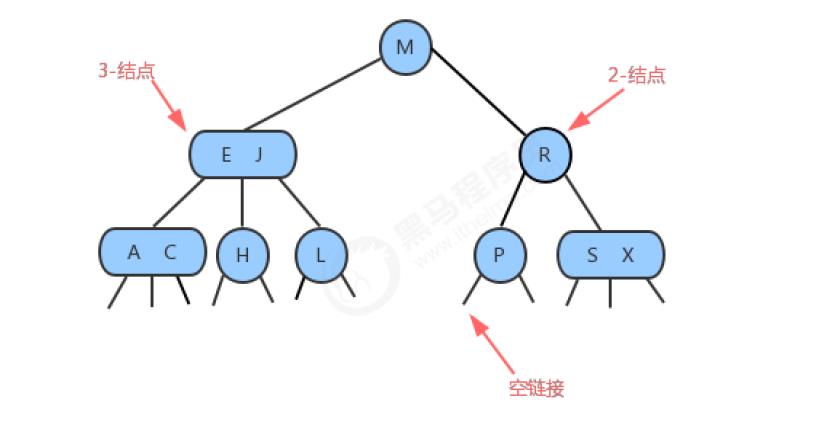
为了保证查找树的平衡性，我们需要一些灵活性，因此在这里我们允许树中的一个结点保存多个键。确切的说，我们将一棵标准的二叉查找树中的结点称为2-结点(含有一个键和两条链)，而现在我们引入3-结点，它含有两个键和三条链。2-结点和3-结点中的每条链都对应着其中保存的键所分割产生的一个区间。

2-3查找树的定义

一棵2-3查找树要么为空，要么满足满足下面两个要求：

2-结点：

• 含有一个键(及其对应的值)和两条链，左链接指向2-3树中的键都小于该结点，右链接指向的2-3树中的键都大于该结点。

3-结点：

• 含有两个键(及其对应的值)和三条链，左链接指向的2-3树中的键都小于该结点，中链接指向的2-3树中的键都位于该结点的两个键之间，右链接指向的2-3树中的键都大于该结点。
  

查找

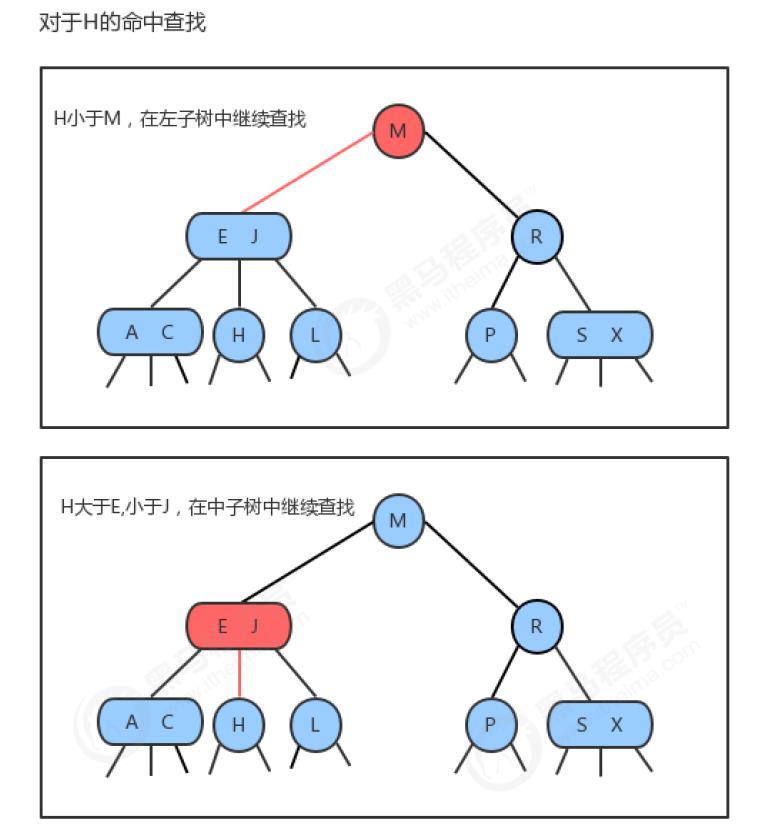
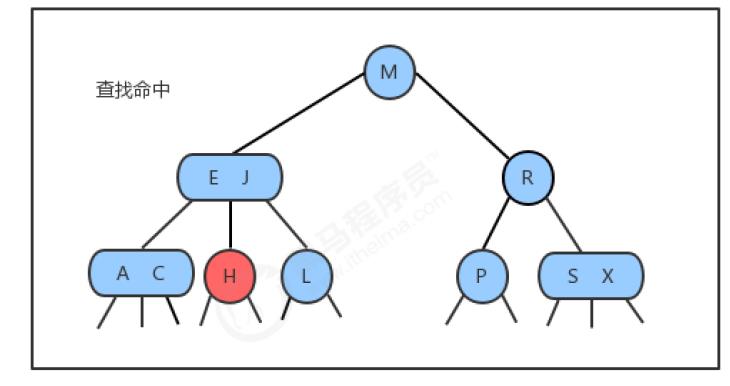
将二叉查找树的查找算法一般化我们就能够直接得到2-3树的查找算法。要判断一个键是否在树中，

1. 我们先将它和根结点中的键比较。如果它和其中任意一个相等，查找命中；
2. 否则我们就根据比较的结果找到指向相应区间的连接，并在其指向的子树中递归地继续查找。
3. 如果这个是空链接，查找未命中。
   
   

插入

往2-3树中插入元素和往二叉查找树中插入元素一样，首先要进行查找，然后将节点挂到未找到的节点上。2-3树之所以能够保证在最差的情况下的效率的原因在于其插入之后仍然能够保持平衡状态

• 向2-结点中插入新键
• 向一棵只含有一个3-结点的树中插入新键
• 向一个父结点为2-结点的3-结点中插入新键
• 向一个父结点为3-结点的3-结点中插入新键
• 分解根结点

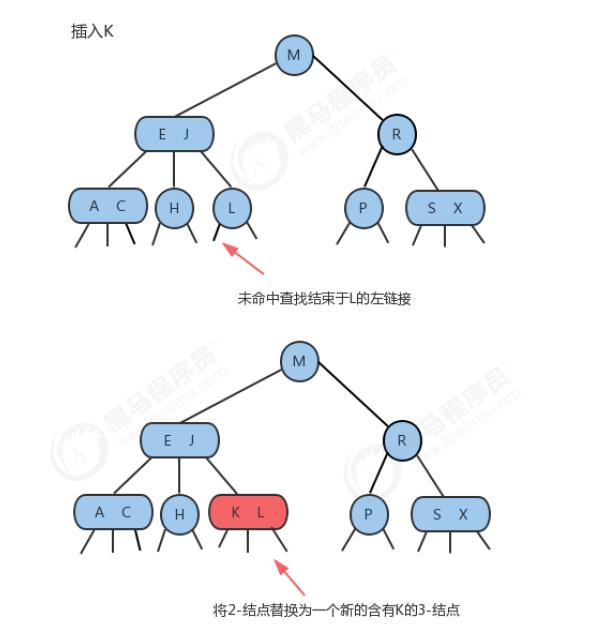
1、 向2-结点中插入新键

如果查找后未找到的节点是一个2-结点，那么很容易，我们只需要将新的元素放到这个2-结点里面使其变成一个3-结点即可。

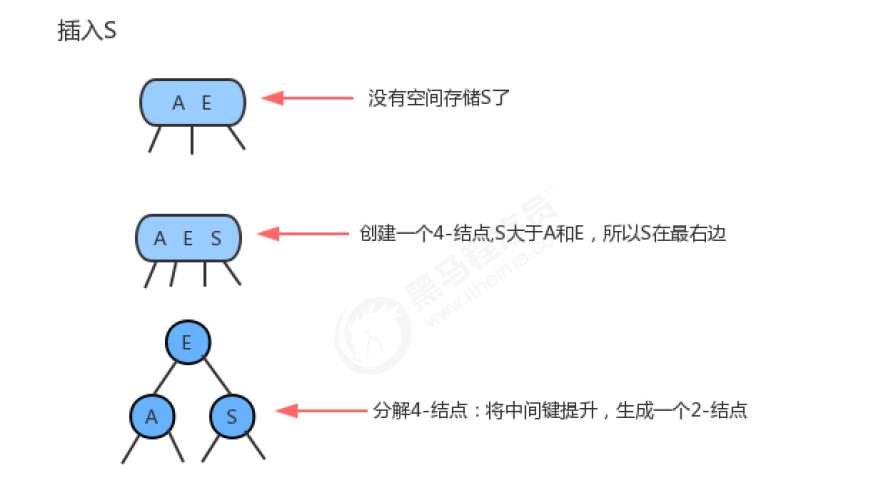
2、向一棵只含有一个3-结点的树中插入新键

假设2-3树只包含一个3-结点，这个结点有两个键，没有空间来插入第三个键了，最自然的方式是我们假设这个结点能存放三个元素，暂时使其变成一个4-结点，同时他包含四条链接。然后，我们将这个4-结点的中间元素提升，左边的键作为其左子结点，右边的键作为其右子结点。插入完成，变为平衡2-3查找树，树的高度从0变为1。

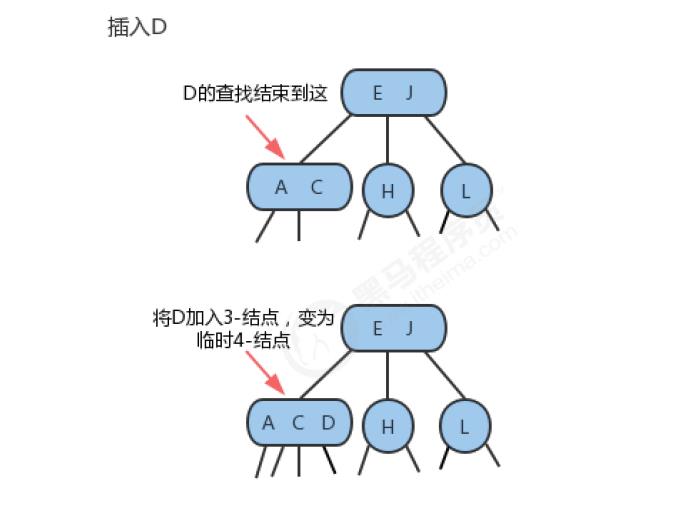
3、向一个父结点为2-结点的3-结点中插入新键

和上面的情况一样一样，我们也可以将新的元素插入到3-结点中，使其成为一个临时的4-结点，然后，将该结点中的中间元素提升到父结点即2-结点中，使其父结点成为一个3-结点，然后将左右结点分别挂在这个3-结点的恰当位置。

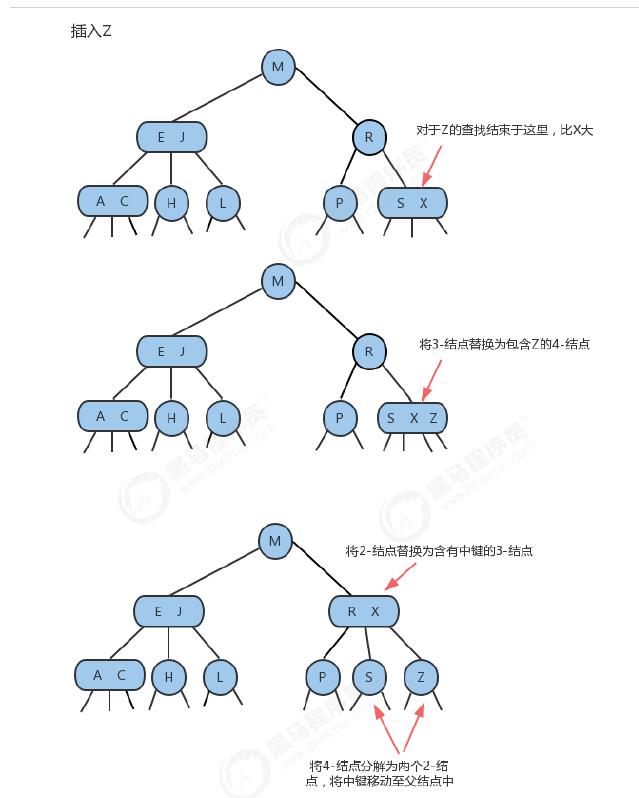
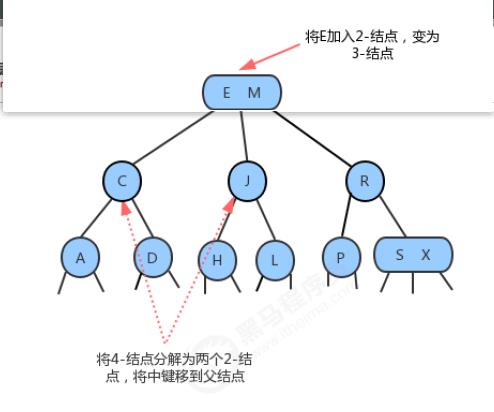
4、向一个父结点为3-结点的3-结点中插入新键

当我们插入的结点是3-结点的时候，我们将该结点拆分，中间元素提升至父结点，但是此时父结点是一个3-结点，插入之后，父结点变成了4-结点，然后继续将中间元素提升至其父结点，直至遇到一个父结点是2-结点，然后将其变为3-结点，不需要继续进行拆分。

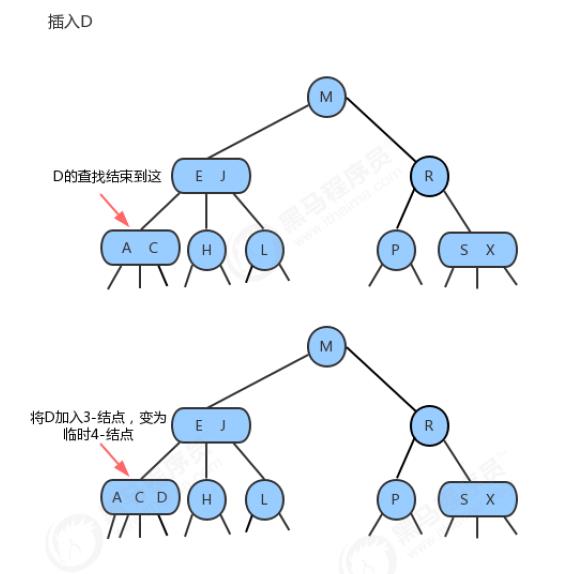
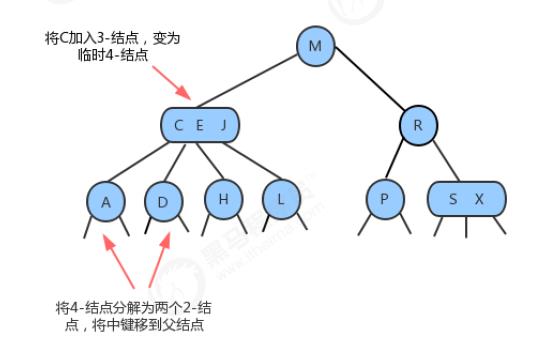
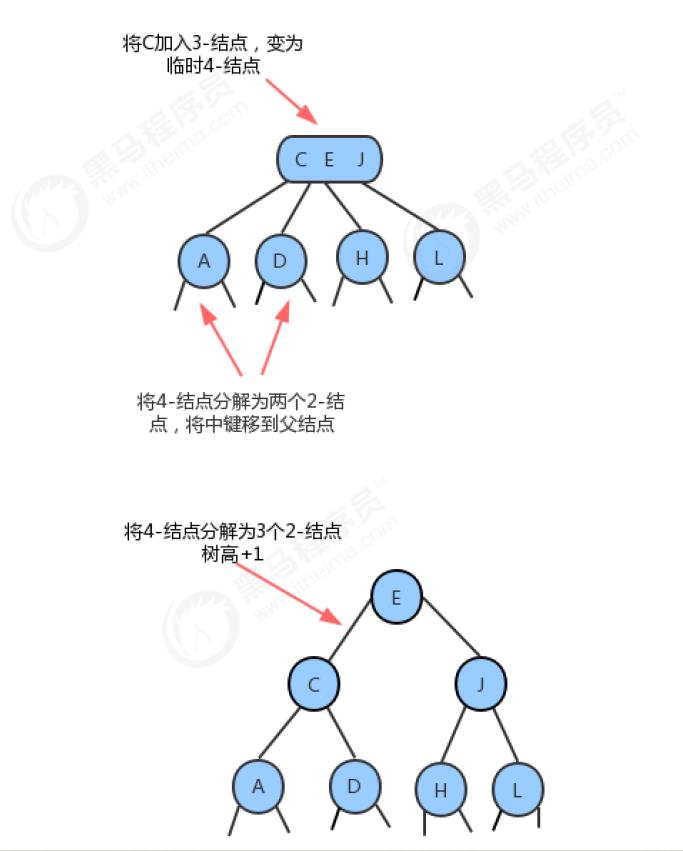
5、分解根结点

当插入结点到根结点的路径上全部是3-结点的时候，最终我们的根结点会编程一个临时的4-结点，此时，就需要将根结点拆分为两个2-结点，树的高度加1。

小结

我们发现在插入的时候，2-3树需要做一些局部的变换来保持2-3树的平衡。

一棵完全平衡的2-3树具有以下性质：

1. 任意空链接到根结点的路径长度都是相等的。
2. 4-结点变换为3-结点时，树的高度不会发生变化，只有当根结点是临时的4-结点，分解根结点时，树高+1。
3. 2-3树与普通二叉查找树最大的区别在于，普通的二叉查找树是自顶向下生长，而2-3树是自底向上生长。

2-3树的实现

• 2-3查找树实现起来比较复杂，在某些情况插入后的平衡操作可能会使得效率降低。但是2-3查找树作为一种比较重要的概念和思路对于我们后面要讲到的红黑树、B树和B+树非常重要。