高级数据结构(Ⅴ)单词查找树(Trie)
Posted 白鳯
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了高级数据结构(Ⅴ)单词查找树(Trie)相关的知识,希望对你有一定的参考价值。
高级数据结构(Ⅴ)单词查找树(Trie)
文章目录

♢前言
单词查找树又称前缀树、字典树、Trie树,常用于检索,大量字符串的排序等。
具体来说,本节中所讨论的算法在一般应用场景中(甚至对于巨型符号表)都能够取得以下性能:
- 查找命中所需要的时间与被查找的键的长度成正比;
- 查找未命中只需检查若干个字符。
以字符串为键的符号表的API如下
public class StringST<Value>
StringST() 创建一个符号表
void put(String key, Value val) 向表中插入键值对(如果值为null,则删除键key)
Value get(String key) 键key所对应的值(如果键不存在返回null)
void delete(String key) 删除键key(和它的值)
boolean contains(String key) 表中是否保存着key的值
boolean isEmpty() 符号表是否为空
String longestPrefixOf(String s) s的前缀中最长的键
Iterable<String> keysWithPrefix(String s) 所有以s为前缀的键
Iterable<String> keysThatMatch(String s) 所有和s匹配的键(+通配符)
int size() 键值对的数量
Iterable<String> keys() 符号表中的所有键
本节符号表所满足的几个基本约定(不接受重复键或空键,值不能为空)
🎈
♢单词查找树
单词查找树由字符串键中的所有字符构造而成,允许使用被查找键中的字符进行查找。它的英文单词trie来自于E.Fredkin在1960年玩的一个文字游戏,因为这个数据结构的作用是取出(retrieval)数据,但发音为try是为了避免与tree混淆。
基本性质
和各种查找树一样,单词查找树也是由链接的结点所组成的数据结构,这些连接可能为空,也可能指向其他结点。每个结点都只可能有一个指向它的结点,称为它的父节点(只有一个结点除外,即根节点,没有任何节点指向根节点)。每个结点都含有R条链接,其中R为字母表的大小(基数)。
单词查找树一般都含有大量的空链接,因此在绘制一颗单词查找树时一般都会忽略空链接。尽管链接指向的是结点,但是也可以看做链接指向的是另一棵单词查找树,它的根节点就是被指向的结点。每条链接都对应着一个字符——因为每条链接都只能指向一个结点,所以可以用链接所对应的字符标记被指向的结点 (根节点除外,因为没有链接指向它)。每个结点也含有一个相应的值,可以是空也可以是符号表中的某个键所关联的值。具体来说,我们将每个键所关联的值保存在该键的最后一个字母所对应的结点中。
值为空的结点在符号表中没有对应的键,它们的存在是为了简化单词查找树的查找操作。
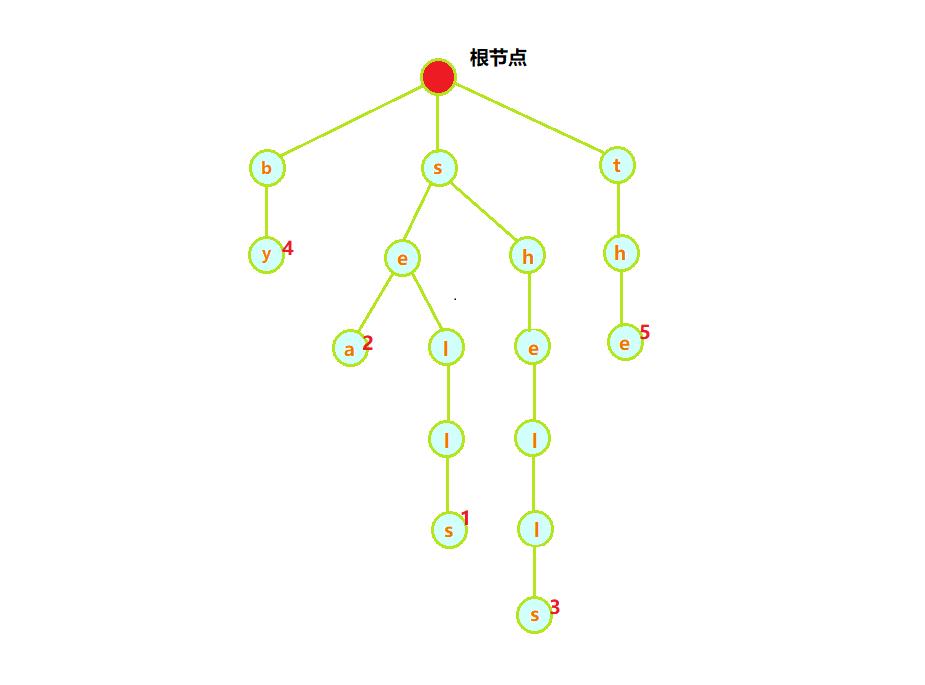
在本节中我们的样例单词查找树是由以下几个单词组成的
[she, sells, sea, shells, by, the],其对应的值为[0, 1, 2, 3, 4, 5]
其对应的单词查找树如下图所示
🎈
查找
在查找时,从根节点开始,首先经过的是键的首字母所对应的链接;在下一个结点中沿着第二个字符所对应的链接继续前进;在第二个结点中沿着第三个字符所对应的链接向前,如此这般直到到达键的最后一个字母所指向的结点或者是遇到了一条空链接。这时会出现以下三种情况:
- 键的尾字符所对应的结点中的值非空(命中)
- 键的尾字符所对用的结点中的值为空(未命中)
- 查找结束于一条空链接
在所用的情况中,执行查找的方式就是在单词查找树中从根结点开始检查某条路径上的所有节点。
🎈
插入
和二叉查找树一样,在插入之前要进行一次查找:在单词查找树中意味着沿着被查找的键的所有字符到达树中表示尾字符的结点或者一个空链接。此时可能会出现以下两种情况:
- 在到达键的尾字符之前就遇到了一个空链接。在这种情况下,单词查找树中不存在与键的尾字符相对应的结点,因此需要为键中还未被检查的每个字符创建一个对应的结点并将键的值保存到最后一个字符的结点中;
- 在遇到空链接之前就到达了键的尾字符。在这种情况下,和关联数组一样,将该结点的值设为键所对应的值(无论该值是否为空)
🎈
删除
从一棵单词查找树中删去一个键值对的第一步是,找到键所对应的结点并将它的值设为空(null)。如果该结点含有一个非空的链接指向某个子结点,那么就不需要再进行其他操作了。如果它的所有链接均为空,那就需要从数据结构中删去这个结点。如果删去它使得它的父节点的所有链接也均为空,就需要继续删除它的父节点,以此类推。
🎈
大小(size())
size()方法的实现有以下三种:
- 即时实现:用一个变量N保存键的数量。
- 更加即时的实现:用结点的实例变量保存子单词查找树中间的数量,在递归的put()和delete()方法调用之后更新它们。
- 延时递归实现:遍历单词查找树中的所有结点并记录非空值结点的总数。
♢算法实现
在展示代码前,我们先来看看结点的表示。
若将结点的空链接考虑进来将会突出单词查找树的以下重要性质:
- 每个结点都含有R个链接,对应着每个可能出现的字符;
- 字符和键均隐式地保存在数据结构中。
在单词查找树中,键是由从根节点到含有非空值的结点的路径所隐式表示的。事实上,数据结构不会存储任何字符串或字符,它保存了链接数组和值。因为参数R的作用的重要性,所以将基于含有R个字符的字母表的单词查找树称为R向单词查找树。
class TrieST<Value> {
//基于单词查找树的符号表
private static int R = 256; //基数
private Node root; //单词查找树的根节点
private int size = 0; //键的个数
private static class Node {
private Object val;
//因为Java不支持泛型数组,所以Node中值的类型必须是Object,可在使用的时候进行强制类型转换
private Node[] next = new Node[R];
}
public Value get(String key) {
Node x = get(root, key, 0);
if (x == null) return null;
return (Value)x.val;
}
private Node get(Node x, String key, int d) {
//返回以x作为根节点的子单词查找树中与key相关联的值
if (x == null) return null;
if (d == key.length()) return x;
char c = key.charAt(d); //找到第d个字符所对应的单词查找树
return get(x.next[c], key, d + 1);
}
public void put(String key, Value val) {
root = put(root, key, val, 0);
}
private Node put(Node x, String key, Value val, int d) {
//如果key存在于以x为根节点的子单词查找树中则更新与它相关的值
if (x == null) {
x = new Node();
}
if (d == key.length()) {
if (x.val == null) {
size += 1;
}
x.val = val;
return x;
}
char c = key.charAt(d); //找到第d个字符所对应的单词查找树
x.next[c] = put(x.next[c], key, val, d + 1);
return x;
}
public void delete(String key) {
root = delete(root, key, 0);
}
private Node delete(Node x, String key, int d) {
if (x == null) {
return null;
}
if (d == key.length()) {
x.val = null;
size -= 1;
} else {
char c = key.charAt(d);
x.next[c] = delete(x.next[c], key, d + 1);
}
if (x.val != null) {
return x;
}
for (char c = 0; c < R; c++) {
if (x.next[c] != null) {
return x;
}
}
return null;
}
public int getSize() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
public Iterable<String> keys() {
return keysWithPrefix("");
}
public Iterable<String> keysWithPrefix(String pre) {
Queue<String> q = new LinkedList<String>();
collect(get(root, pre, 0), pre, q);
return q;
}
private void collect(Node x, String pre, Queue<String> q) {
if (x == null) return;
if (x.val != null) {
q.offer(pre);
}
for (char c = 0; c < R; c++) {
collect(x.next[c], pre + c, q);
}
}
public boolean contains(String key) {
return contains(root, key, 0);
}
private boolean contains(Node x, String key, int d) {
if (x == null) {
return false;
}
if (d == key.length() && x.val != null) {
return true;
}
char c = key.charAt(d);
return contains(x.next[c], key, d + 1);
}
public Iterable<String> keysThatMatch(String pat) {
//通配符(.)
Queue<String> q = new LinkedList<>();
collect(root, "", pat, q);
return q;
}
private void collect(Node x, String pre, String pat, Queue<String> q) {
int d = pre.length();
if (x == null) {
return;
}
if (d == pat.length() && x.val != null) {
q.offer(pre);
}
if (d == pat.length()) {
return;
}
char next = pat.charAt(d);
for (char c = 0; c < R; c++) {
if (next == '.' || next == c) {
collect(x.next[c], pre + c, pat, q);
}
}
}
public String longestPrefixOf(String s) {
int length = search(root, s, 0, 0);
return s.substring(0, length);
}
private int search(Node x, String s, int d, int length) {
if (x == null) {
return length;
}
if (x.val != null) {
length = d;
}
if (d == s.length()) {
return length;
}
char c = s.charAt(d);
return search(x.next[c], s, d + 1, length);
}
}
测试代码如下
public class TrieTest {
public static void main(String[] args) {
String[] strs = {"she", "sells", "sea", "shells", "by", "the"};
TrieST<Integer> trie = new TrieST<Integer>();
//将strs中的值和下标作为键值对加入前缀树中
for (int i = 0; i < strs.length; i++) {
trie.put(strs[i], i);
}
//返回键“sea”对应的值
int sea_val = trie.get("sea");
System.out.println(">键“sea”对应的值为:" + sea_val);
//符号表中是否保存着“the”的值
boolean the_val = trie.contains("the");
System.out.println(">是否保存the的值: " + the_val);
//符号表是否为空
boolean isEmpty = trie.isEmpty();
System.out.println(">符号表是否为空: " + isEmpty);
//所有键
LinkedList<String> keys = (LinkedList<String>) trie.keys();
System.out.println(">符号表中的所有键为: ");
while (!keys.isEmpty()) {
System.out.print(keys.poll() + " , ");
}
//"sellsaaaa"的最长前缀
String se_longest = trie.longestPrefixOf("sellsaaaa");
System.out.println("\\n>sellsaaaa最长前缀为: " + se_longest);
//所有以“s”为前缀的键
LinkedList<String> pre_keys = (LinkedList<String>) trie.keysWithPrefix("s");
System.out.println(">以s为前缀的键有:");
while (!pre_keys.isEmpty()) {
System.out.print(pre_keys.poll() + " , ");
}
//所有匹配".he"的键
LinkedList<String> pat_keys = (LinkedList<String>) trie.keysThatMatch(".he");
System.out.println("\\n>匹配.he的键为:");
while (!pat_keys.isEmpty()) {
System.out.print(pat_keys.poll() + " , ");
}
System.out.println("\\n>符号表中键的个数为:" + trie.getSize());
//删除键sea它的值
trie.delete("sea");
System.out.println(">符号表中是否包含键sea: " + trie.contains("sea"));
System.out.println(">符号表中键的个数为:" + trie.getSize());
}
}
相应输出结果如下
>键“sea”对应的值为:2
>是否保存the的值: true
>符号表是否为空: false
>符号表中的所有键为:
by , sea , sells , she , shells , the ,
>sellsaaaa最长前缀为: sells
>以s为前缀的键有:
sea , sells , she , shells ,
>匹配.he的键为:
she , the ,
>符号表中键的个数为:6
>符号表中是否包含键sea: false
>符号表中键的个数为:5
♢单词查找树的性质
单词查找树的链表结构(形状)和键的插入或者删除顺序无关:对于任意给定的一组键,其单词查找树都是唯一的。
在单词查找树中查找一个键或是插入一个键时,访问数组的次数最多为键的长度+1。
字母表的大小为R,在一棵由N个随机键构造的单词查找树中,未命中查找平均所需检查的结点数量为logRN(以R为底N的对数)
查找未命中的成本与键的长度无关。
一棵单词查找树中的链接总数在
RN到RNw之间,其中w为键的平均长度。
- 当所有键均较短时,链接的总数接近于
RN - 当所有键均较长时,链接的总数接近于
RNw - 缩小
R能够节省大量的空间
♢三向单词查找树
为了避免R向单词查找树过度的空间消耗,接下来学习另一种数据的表示方法:三向单词查找树(TST)。在三向单词查找树中,每个结点都含有一个字符,三条链接和一个值。这三条链接分别对应着当前字母小于、等于和大于结点字母的所有键。
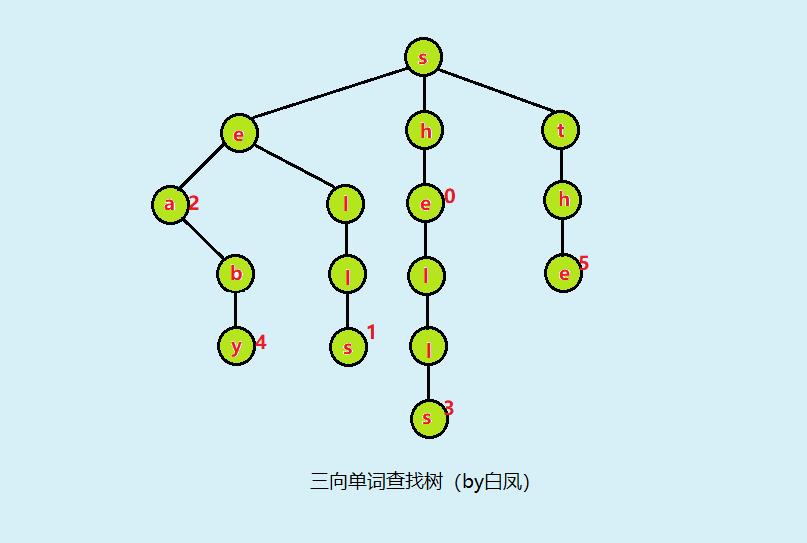
[she, sells, sea, shells, by, the],其对应的值为[0, 1, 2, 3, 4, 5]
按顺序插入上面的键值对所构成的三向单词查找树如下
🎈
基于三向单词查找树的符号表
class TST<Value> {
//基于三向单词查找树的符号表
private Node root;
private class Node {
char c; //字符
Node left, mid, right; //左中右三向单词查找树
Value val; //和字符串相关联的值
}
public Value get(String key) {
Node x = get(root, key, 0);
if (x == null) {
return null;
}
return (Value)x.val;
}
private Node get(Node x, String key, int d) {
if (x == null) {
return null以上是关于高级数据结构(Ⅴ)单词查找树(Trie)的主要内容,如果未能解决你的问题,请参考以下文章