二叉查找树

Posted 2020-07-29 狮子座明仔

二叉查找树（binary search tree，又叫二叉搜索树或者二叉排序树）是一种非常重要的数据结构，许多高级树结构都是二叉查找树的变种，例如AVL树、红黑树等，理解二叉查找树对于后续树结构的学习有很好的作用。同时利用二叉查找树可以进行排序，称为二叉排序，也是很重要的一种思想。

本文主要参考算法导论，详细介绍二叉查找树的原理及具体的python和java代码实现。

1.定义

查找树是一种数据结构,它支持多种动态集合操作,包括search,minimum,maximum,predecessor,successor,insert以及delete。它既可以用作字典，也可以用作优先队列。

wiki的描述：

二叉树查找的性质：
1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2. 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3. 任意节点的左、右子树也分别为二叉查找树。 没有键值相等的节点（no duplicate nodes）。
4. 二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为O(log n)。

二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、multiset、关联数组等。
虽然二叉查找树的最坏效率是O(n),但它支持动态查询,且有很多改进版的二叉查找树可以使树高为O(logn),如SBT,AVL,红黑树等.

二.python实现

以下面图示的二叉树为例说明查找算法

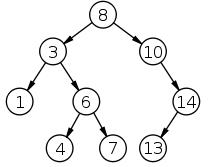
Node 类

创建一个类，命名为Node，做为二叉树节点结构，其中包括：左枝、右枝、节点数据三个变量。

class Node:
    """
    二叉树左右枝
    """
    def __init__(self, data):
        """
        节点结构

        """
        self.left = None
        self.right = None
        self.data = data

例如创建一个含整数8的节点。因为仅仅创建一个节点，所以左右枝都是None。

root = Node(8)

这样就得到如下图所示的只有一个节点的树。

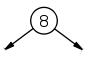
插入方法

现在已经有了一棵光秃秃的树，要有枝杈和叶子，就必须用插入数据方法，添加新的节点和数据。

def insert(self, data):
    """
    插入节点数据
    """
    if data < self.data:
        if self.left is None:
            self.left = Node(data)
        else:
            self.left.insert(data)
    elif data > self.data:
        if self.right is None:
            self.right = Node(data)
        else:
            self.right.insert(data)

承接前面的操作，可以用下面的方式增加树的枝杈和叶子（左右枝以及节点数据）。

root.insert(3)
root.insert(10)
root.insert(1)

当增加了第二个节点数据3,程序会：

• 第一步，root会调用insert()，其参数是data=3
• 第二步，比较3和8（已有的根节点），3比8小。并且树的左枝还是None，于是就在左边建立一个新的节点。

增加第三个节点数据10,程序会：

• 第一步，跟前面的第一步一样，只不过data=10
• 第二步，发现10大于8,同时右边是None,于是就把它做为右边新建分支的节点数据。

增加第四个节点数据1,程序会：

• 第一步，同前，data=1
• 第二步，1小于8,所以要放在树的左枝；
• 第三步，左枝已经有子节点3,该节点再次调用insert()方法，1小于3,所以1就做为3的子节点，且放在原本就是None的左侧。

如此，就形成了下图的树

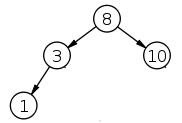
继续增加节点数据

root.insert(6)
root.insert(4)
root.insert(7)
root.insert(14)
root.insert(13)

最终形成下图的树

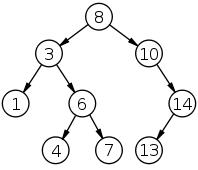
遍历树

此方法用于查找树中的某个节点，如果找到了，就返回该节点，否则返回None。为了方便，也返回父节点。

def lookup(self, data, parent=None):
    """
    遍历二叉树
    """
    if data < self.data:
        if self.left is None:
            return None, None
        return self.left.lookup(data, self)
    elif data > self.data:
        if self.right is None:
            return None, None
        return self.right.lookup(data, self)
    else:
        return self, parent

测试一下，找一找数据为6的节点

node, parent = root.lookup(6)

调用lookup()后，程序会这么干：

1. 调用lookup()，传递参数data=6,默认parent=None
2. data=6，小于根节点的值8
3. 指针转到根节点左侧，此时:data=6,parent=8,再次调用lookup()
4. data=6大于左侧第一层节点数据3
5. 指针转到3的右侧分支，data=6,parent=3,再次调用lookup()
6. 节点数据等于6,于是返回这个节点和它的父节点3

删除方法

删除节点数据。代码如下：

def delete(self, data):
    """
    删除节点
    """
    node, parent = self.lookup(data)        #已有节点
    if node is not None:
        children_count = node.children_count()      #判断子节点数
        if children_count == 0:
            # 如果该节点下没有子节点，即可删除
            if parent.left is node:
                parent.left = None
            else:
                parent.right = None
            del node
        elif children_count == 1:
            # 如果有一个子节点，则让子节点上移替换该节点（该节点消失)
            if node.left:
                n = node.left
            else:
                n = node.right
            if parent:
                if parent.left is node:
                    parent.left = n
                else:
                    parent.right = n
            del node
        else:
            # 如果有两个子节点，则要判断节点下所有叶子
            parent = node
            successor = node.right
            while successor.left:
                parent = successor
                successor = successor.left
            node.data = successor.data
            if parent.left == successor:
                parent.left = successor.right
            else:
                parent.right = successor.right

在上述方法中，得到当前节点下的子节点数目后，需要进行三种情况的判断

• 如果没有子节点，直接删除
• 如果有一个子节点，要将下一个子节点上移到当前节点，即替换之
• 如果有两个子节点，要对自己点的数据进行判断，并从新安排节点排序

上述方法中用到了统计子节点数目的方法，代码如下：

def children_count(self):
    """
    子节点个数
    """
    cnt = 0
    if self.left:
        cnt += 1
    if self.right:
        cnt += 1
    return cnt

例1：删除数据为1的节点，它是3的子节点，1后面没有子节点

root.delete(1)

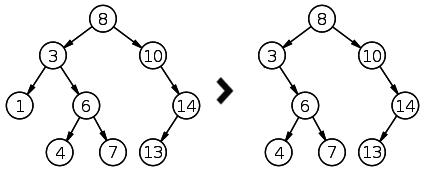
比较两个二叉树

比较两个二叉树的方法中，只要有一个节点（叶子）与另外一个树的不同，就返回False，也包括缺少对应叶子的情况。

def compare_trees(self, node):
    """
    比较两棵树
    """
    if node is None:
        return False
    if self.data != node.data:
        return False
    res = True
    if self.left is None:
        if node.left:
            return False
    else:
        res = self.left.compare_trees(node.left)
    if res is False:
        return False
    if self.right is None:
        if node.right:
            return False
    else:
        res = self.right.compare_trees(node.right)
    return res

例如，比较tree(3,8,10)和tree(3,8,11)

root2 是tree(3,8,11)的根
root 是tree(3,8,10)的根
root.compare_trees(root2)

执行上面的代码，程序会这么走：

1. root调用compare_trees()方法
2. root有左侧子节点，调用该节点的compare_trees()
3. 两个左侧子节点比较，返回true
4. 按照前面的过程，比较右侧节点，发现不同，则返回False

打印树

把二叉树按照一定的顺序打印出来。不需要参数了。做法就是先左后右（左小于右）。

def print_tree(self):
    """
    按顺序打印数的内容
    """
    if self.left:
        self.left.print_tree()
    print self.data,
    if self.right:
        self.right.print_tree()

操作一下：

root.print_tree()

输出： 1, 3, 4, 6, 7, 8, 10, 13, 14

包含所有树元素的生成器

创建一个包含所有树元素的生成器，有时候是有必要的。考虑到内存问题，没有必要实时生成所有节点数据列表，而是要每次调用此方法时，它返回的下一个节点的值。为此，使用它返回一个对象，并停止在那里，那么该函数将在下一次调用方法时从那里继续通过yield关键字返回值。在这种情况下，要使用堆栈，不能使用递归。

def tree_data(self):
    """
    二叉树数据结构
    """
    stack = []
    node = self
    while stack or node: 
        if node:
            stack.append(node)
            node = node.left
        else: 
            node = stack.pop()
            yield node.data
            node = node.right

举例，通过循环得到树：

for data in root.tree_data():
    print data

程序会按照先左后右边的原子将数据入栈、出栈，顺序取出值，并返回结果。

三.java实现

插入操作

二叉树查找树b插入操作x的过程如下：

1、若b是空树，则直接将插入的结点作为根结点插入。
2、x等于b的根结点的数据的值，则直接返回，否则。
3、若x小于b的根结点的数据的值，则将x要插入的结点的位置改变为b的左子树，否则。 4、将x要出入的结点的位置改变为b的右子树。

/**插入元素*/
   public void insert(T t)
   {
       rootTree = insert(t, rootTree);
   }
/**在某个位置开始判断插入元素*/
   public BinaryNode<T> insert(T t,BinaryNode<T> node)
   {
       if(node==null)
       {
           //新构造一个二叉查找树
           return new BinaryNode<T>(t, null, null);
       }
       int result = t.compareTo(node.data);
       if(result<0)
          node.left= insert(t,node.left);
       else if(result>0)
          node.right= insert(t,node.right);
       else
           ;//doNothing
       return node;
   }

查找操作

在二叉查找树中查找x的过程如下：

1、若二叉树是空树，则查找失败。
2、若x等于根结点的数据，则查找成功，否则。
3、若x小于根结点的数据，则递归查找其左子树，否则。
4、递归查找其右子树。

根据上述的步骤，写出其查找操作的代码。

/**查找指定的元素,默认从
    * 根结点出开始查询*/
   public boolean contains(T t)
   {
      return contains(t, rootTree);

   }
 /**从某个结点出开始查找元素*/
   public boolean contains(T t, BinaryNode<T> node)
   {
      if(node==null)
        return false;//结点为空，查找失败
      int result = t.compareTo(node.data);
       if(result>0)
          return contains(t,node.right);//递归查询右子树
      else if(result<0)
          return contains(t, node.left);//递归查询左子树  
      else
          return true;
   }
    /**
       这里我提供一个对二叉树最大值
       最小值的搜索*/


 /**找到二叉查找树中的最小值*/
   public T findMin()
   {
      if(isEmpty())
      {
          System.out.println("二叉树为空");
          return null;
      }else
       return findMin(rootTree).data;

   }
   /**找到二叉查找树中的最大值*/
   public T findMax()
   {
       if(isEmpty())
          {
              System.out.println("二叉树为空");
              return null;
          }else
           return findMax(rootTree).data;
   }

/**查询出最小元素所在的结点*/
   public BinaryNode<T> findMin(BinaryNode<T> node)
   {
       if(node==null)
           return null;
       else if(node.left==null)
           return node;
       return findMin(node.left);//递归查找
   }
   /**查询出最大元素所在的结点*/
   public BinaryNode<T> findMax(BinaryNode<T> node)
   {
       if(node!=null)
       {
           while(node.right!=null)
               node=node.right;
       }
       return node;       
   }

经典二叉树查找算法

自用无bug的二叉树算法代码：

int BinarySearch(int array[], int n, int value)
{
    int left = 0;
    int right = n - 1;
    //如果这里是int right = n 的话，那么下面有两处地方需要修改，以保证一一对应：
    //1、下面循环的条件则是while(left < right)
    //2、循环内当 array[middle] > value 的时候，right = mid

    while (left <= right)  //循环条件，适时而变
    {
        int middle = left + ((right - left) >> 1);  //防止溢出，移位也更高效。同时，每次循环都需要更新。

        if (array[middle] > value)
        {
            right = middle - 1;  //right赋值，适时而变
        }
        else if(array[middle] < value)
        {
            left = middle + 1;
        }
        else
            return middle;
        //可能会有读者认为刚开始时就要判断相等，但毕竟数组中不相等的情况更多
        //如果每次循环都判断一下是否相等，将耗费时间
    }
    return -1;
}

jdk 中的二叉树查找算法：

    /**
     *
     * @Title: jdk 自带的Arrays的二叉树查找实现代码
     * @Description: 在a数组中找key，并返回其位置
     * @date:2016/6/22 19:16
     * @param
     * @return
     */
    // Like public version, but without range checks.
    private static int binarySearch0(Object[] a, int fromIndex, int toIndex,
                                     Object key) {
        int low = fromIndex;
        int high = toIndex - 1;

        while (low <= high) {
            int mid = (low + high) >>> 1;
            @SuppressWarnings("rawtypes")
            Comparable midVal = (Comparable)a[mid];
            @SuppressWarnings("unchecked")
            int cmp = midVal.compareTo(key);

            if (cmp < 0)
                low = mid + 1;
            else if (cmp > 0)
                high = mid - 1;
            else
                return mid; // key found
        }
        return -(low + 1);  // key not found.
    }

以上java和python的详细实现代码见我的github。

参考文章：http://www.laurentluce.com/posts/binary-search-tree-library-in-python/comment-page-1/