⭐算法入门⭐《二叉树 - 二叉搜索树》简单10 —— LeetCode 剑指 Offer 54. 二叉搜索树的第k大节点

Posted 2021-10-08 英雄哪里出来

文章目录

• 一、题目
• • 1、题目描述
  • 2、基础框架
  • 3、原题链接
• 二、解题报告
• • 1、思路分析
  • 2、时间复杂度
  • 3、代码详解
• 三、本题小知识
• 四、加群须知

一、题目

1、题目描述

  给定一棵二叉搜索树，请找出其中第k大的节点。
  样例输入： root = [5,3,6,2,4,null,null,1], k = 3
  样例输出： 2

2、基础框架

• C语言 版本给出的基础框架代码如下：

int kthLargest(struct TreeNode* root, int k) {
}

3、原题链接

LeetCode 剑指 Offer 54. 二叉搜索树的第k大节点

二、解题报告

1、思路分析

  直接利用中序遍历生成一个递增序列以后，假设总共 $n$ 个结点，那么第 k 大的就是数组中第 $n-k$ 个元素。

2、时间复杂度

  每个结点都需要访问，时间复杂度为 $O(n)$。

3、代码详解

#define maxn 500005
int val[maxn];
int n;

void inorder(struct TreeNode* root) {
    if(!root) {
        return ;
    }
    inorder(root->left);
    val[n++] = root->val;            // (1)
    inorder(root->right);
}

int kthLargest(struct TreeNode* root, int k){
    n = 0;
    inorder(root);
    return val[n-k];                 // (2)
}

• $(1)$ 中序遍历，并且将结点存储到 val 数组中；
• $(2)$ 逆向索引第 $k$ 大元素；

---

三、本题小知识

  二叉搜索树的中序遍历的结果为该二叉搜索树的递增序列。

---

四、加群须知

  相信看我文章的大多数都是「 大学生 」，能上大学的都是「 精英 」，那么我们自然要「 精益求精 」，如果你还是「 大一 」，那么太好了，你拥有大把时间，当然你可以选择「 刷剧 」，然而，「 学好算法 」，三年后的你自然「 不能同日而语 」。
  那么这里，我整理了「 几十个基础算法 」 的分类，点击开启：

🌌《算法入门指引》🌌
  如果链接被屏蔽，或者有权限问题，可以私聊作者解决。

  大致题集一览：





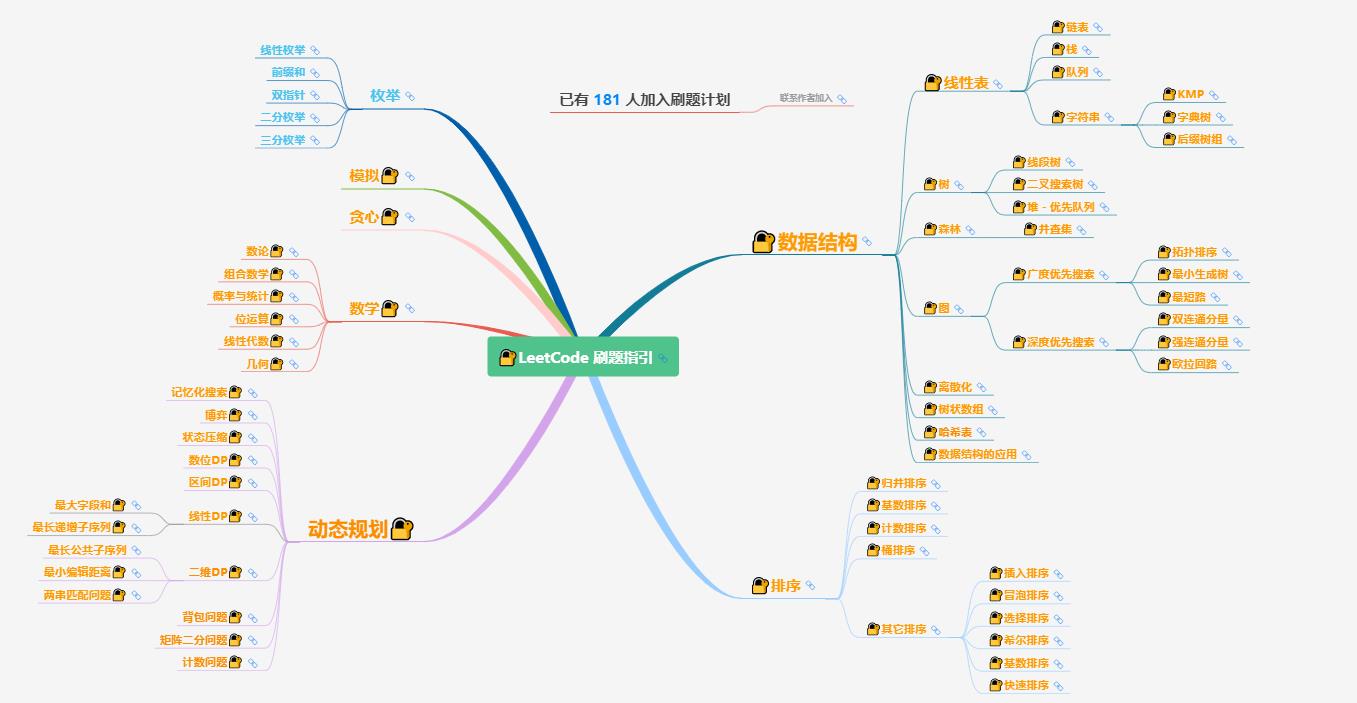
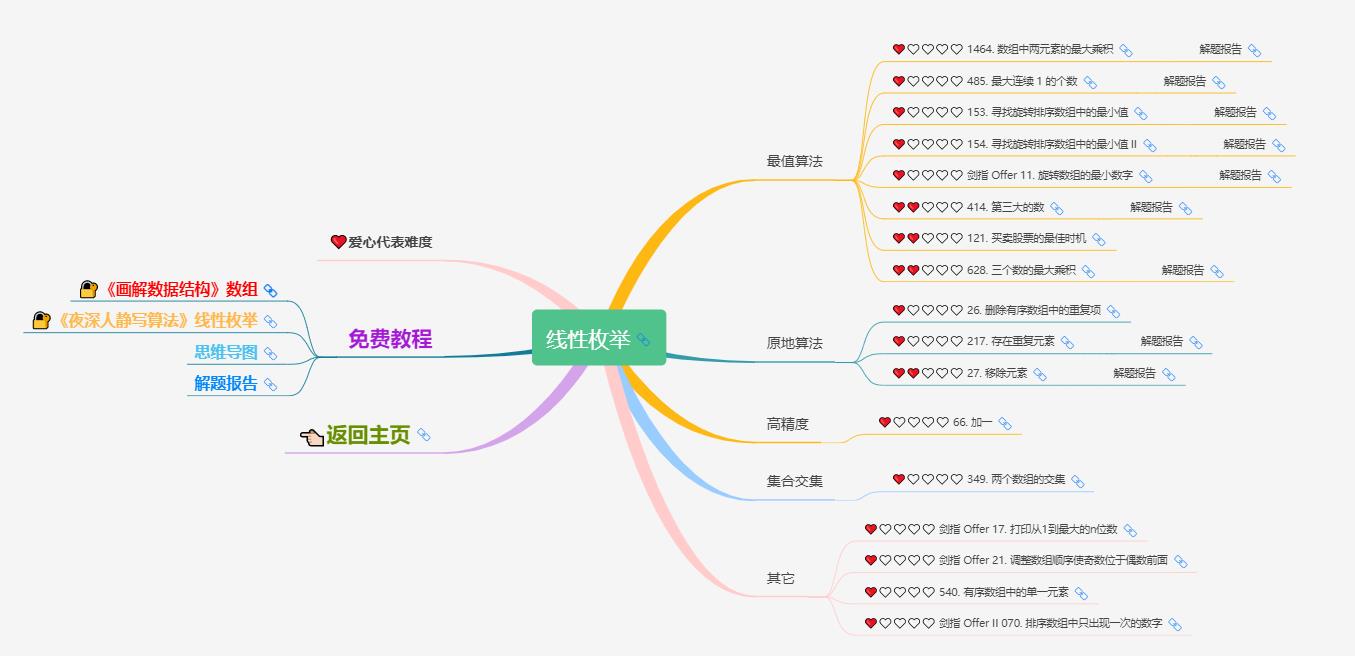
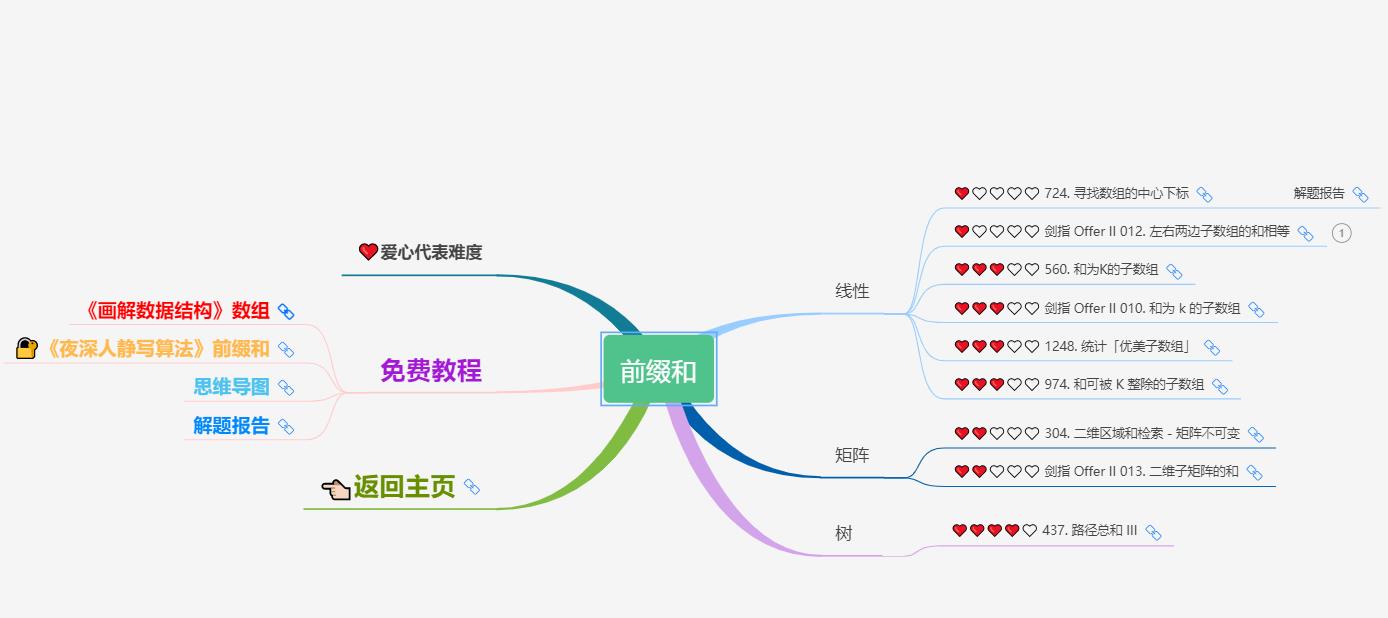
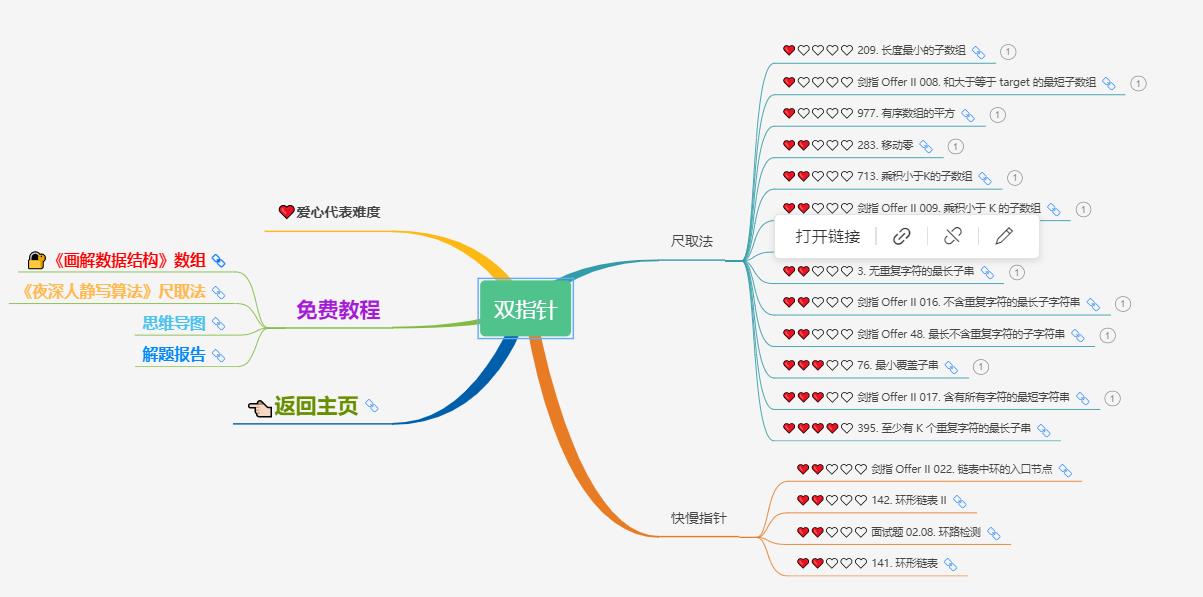
  为了让这件事情变得有趣，以及「 照顾初学者 」，目前题目只开放最简单的算法 「 枚举系列 」 （包括：线性枚举、双指针、前缀和、二分枚举、三分枚举），当有 一半成员刷完 「 枚举系列 」 的所有题以后，会开放下个章节，等这套题全部刷完，你还在群里，那么你就会成为「 夜深人静写算法 」专家团 的一员。
  不要小看这个专家团，三年之后，你将会是别人 望尘莫及 的存在。如果要加入，可以联系我，考虑到大家都是学生， 没有「 主要经济来源 」，在你成为神的路上，「 不会索取任何 」。
  🔥联系作者，或者扫作者主页二维码加群，加入刷题行列吧🔥

---

🔥让天下没有难学的算法🔥
C语言免费动漫教程，和我一起打卡！ 🌞《光天化日学C语言》🌞
入门级C语言真题汇总 🧡《C语言入门100例》🧡
几张动图学会一种数据结构 🌳《画解数据结构》🌳
组团学习，抱团生长 🌌《算法入门指引》🌌
竞赛选手金典图文教程 💜《夜深人静写算法》💜