排序--08---堆排序

Posted 2021-10-03 高高for 循环

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了排序--08---堆排序相关的知识，希望对你有一定的参考价值。

文章目录

堆排序
堆构造过程
堆排序过程
堆排序总的代码
- 测试:

堆排序

需求:

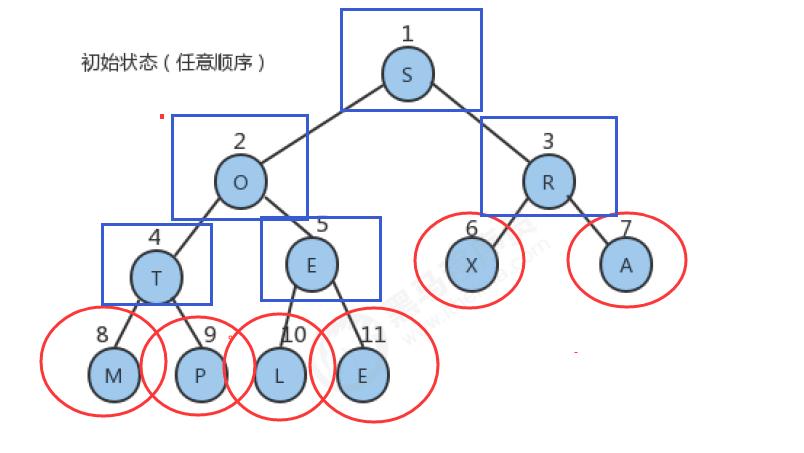
给定一个数组：String[] arr = {“S”,“O”,“R”,“T”,“E”,“X”,“A”,“M”,“P”,“L”,“E”}
请对数组中的字符按从小到大排序。

实现步骤：

构造堆；
得到堆顶元素，这个值就是最大值；
交换堆顶元素和数组中的最后一个元素，此时所有元素中的最大元素已经放到合适的位置；
对堆进行调整，重新让除了最后一个元素的剩余元素中的最大值放到堆顶；
重复2~4这个步骤，直到堆中剩一个元素为止。

API设计：

堆构造过程

树–07—堆的实现

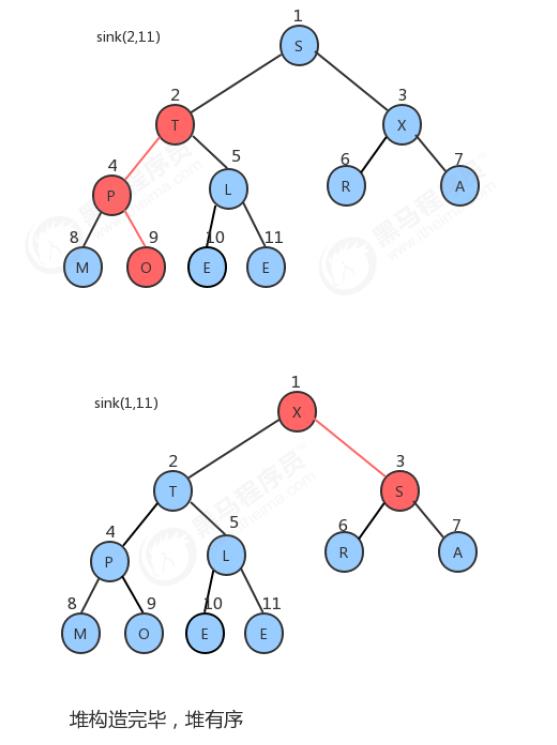
堆的构造，最直观的想法就是另外再创建一个和新数组数组，然后从左往右遍历原数组，每得到一个元素后，添加到新数组中，并通过上浮，对堆进行调整，最后新的数组就是一个堆。
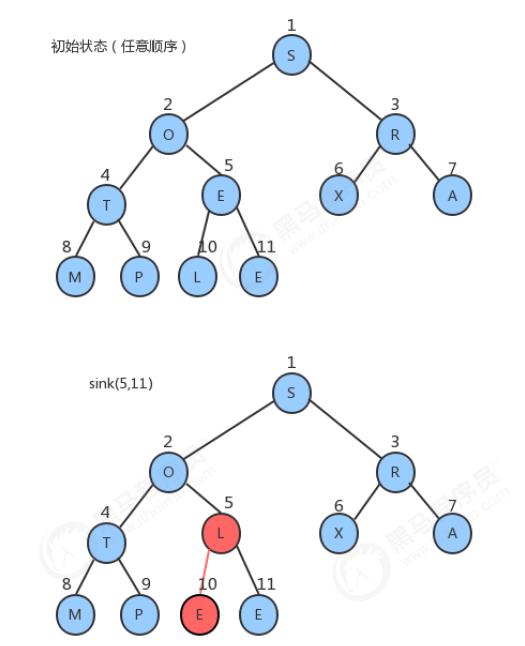
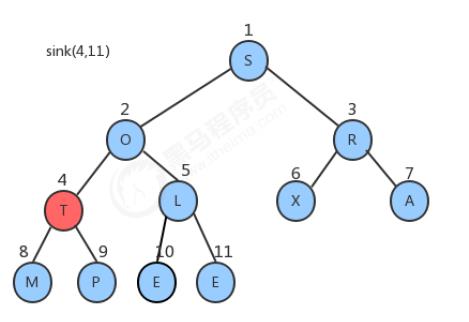
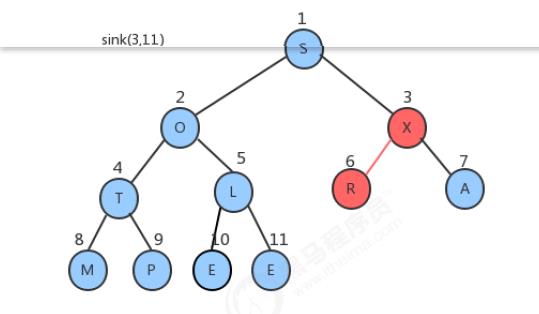
上述的方式虽然很直观，也很简单，但是我们可以用更聪明一点的办法完成它。创建一个新数组，把原数组0 ~ length-1的数据拷贝到新数组的1~length处，再从新数组长度的一半处开始往1索引处扫描（从右往左），然后对扫描到的每一个元素做下沉调整即可。

因为堆数组中的一半是叶子节点,一半是非叶子节点.

堆数组中最大索引处的父节点,就是最后一个非叶子节点

图解流程:

代码实现

public class HeapSort {
    //判断heap堆中索引i处的元素是否小于索引j处的元素
    private static  boolean less(Comparable[] heap, int i, int j) {
        return heap[i].compareTo(heap[j])<0;
    }

    //交换heap堆中i索引和j索引处的值
    private static  void exch(Comparable[] heap, int i, int j) {
        Comparable tmp = heap[i];
        heap[i] = heap[j];
        heap[j] = tmp;
    }



    //根据原数组source，构造出堆heap
    private static void createHeap(Comparable[] source, Comparable[] heap) {
        //把source中的元素拷贝到heap中，heap中的元素就形成一个无序的堆
        System.arraycopy(source,0,heap,1,source.length);

        //对堆中的元素做下沉调整(从长度的一半处开始，往索引1处扫描)
        for (int i = (heap.length)/2;i>0;i--){
            sink(heap,i,heap.length-1);
        }

    }


    //在heap堆中，对target处的元素做下沉，范围是0~range
    private static void sink(Comparable[] heap, int target, int range){

        while(2*target<=range){
            //1.找出当前结点的较大的子结点
            int max;
            if (2*target+1<=range){
                if (less(heap,2*target,2*target+1)){
                    max = 2*target+1;
                }else{
                    max = 2*target;
                }
            }else{
                max = 2*target;
            }

            //2.比较当前结点的值和较大子结点的值
            if (!less(heap,target,max)){
                break;
            }

            exch(heap,target,max);

            target = max;
        }
    }

}

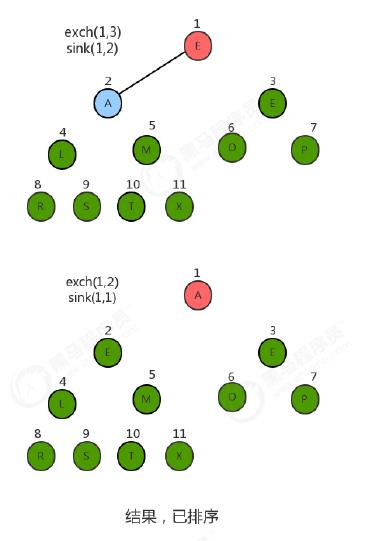
堆排序过程

排序流程:

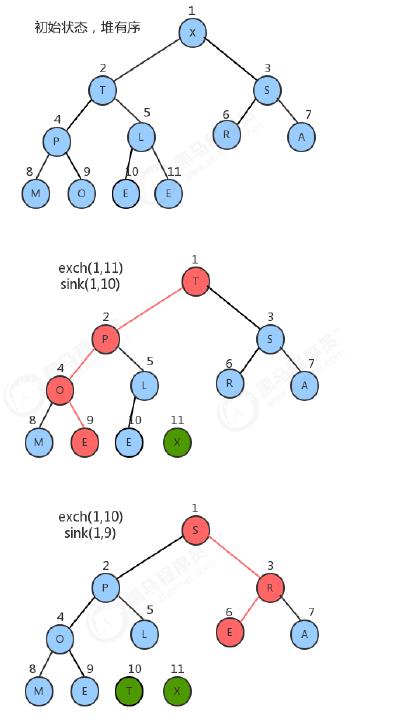
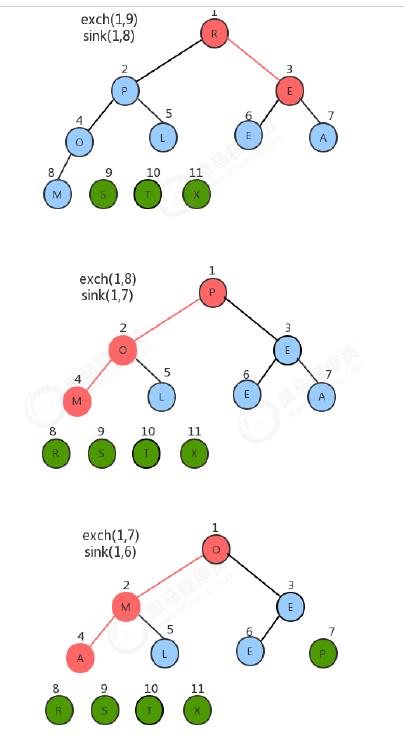
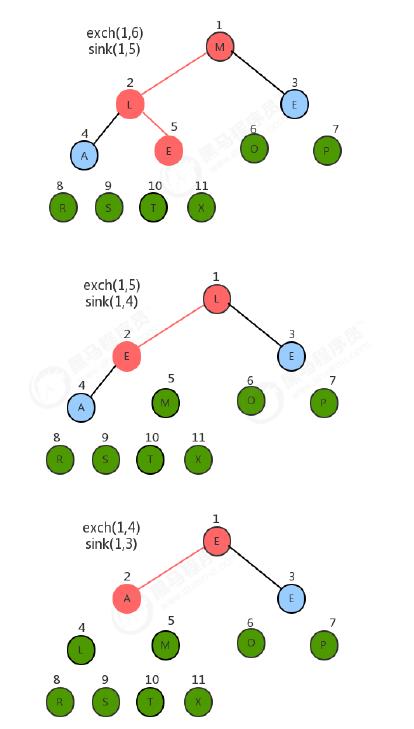
对构造好的堆，我们只需要做类似于堆的删除操作，就可以完成排序。

将堆顶元素和堆中最后一个元素交换位置；
通过对堆顶元素下沉调整堆，把最大的元素放到堆顶(此时最后一个元素不参与堆的调整，因为最大的数据已经到了数组的最右边)
重复1~2步骤，直到堆中剩最后一个元素。

图解流程:

代码实现:

  //对source数组中的数据从小到大排序
    public static  void sort(Comparable[] source) {
        //构建堆
        Comparable[] heap = new Comparable[source.length+1];
        createHeap(source,heap);
        //定义一个变量，记录未排序的元素中最大的索引
        int N = heap.length-1;
        //通过循环，交换1索引处的元素和排序的元素中最大的索引处的元素
        while(N!=1){
            //交换元素
            exch(heap,1,N);
            //排序交换后最大元素所在的索引，让它不要参与堆的下沉调整
            N--;
            //需要对索引1处的元素进行对的下沉调整
            sink(heap,1, N);
        }

        //把heap中的数据复制到原数组source中
        System.arraycopy(heap,1,source,0,source.length);

    }

堆排序总的代码

package main.java.Algorithms.heap;

public class HeapSort {
    //判断heap堆中索引i处的元素是否小于索引j处的元素
    private static  boolean less(Comparable[] heap, int i, int j) {
        return heap[i].compareTo(heap[j])<0;
    }

    //交换heap堆中i索引和j索引处的值
    private static  void exch(Comparable[] heap, int i, int j) {
        Comparable tmp = heap[i];
        heap[i] = heap[j];
        heap[j] = tmp;
    }



    //根据原数组source，构造出堆heap
    private static void createHeap(Comparable[] source, Comparable[] heap) {
        //把source中的元素拷贝到heap中，heap中的元素就形成一个无序的堆
        System.arraycopy(source,0,heap,1,source.length);

        //对堆中的元素做下沉调整(从长度的一半处开始，往索引1处扫描)
        for (int i = (heap.length)/2;i>0;i--){
            sink(heap,i,heap.length-1);
        }

    }



    //对source数组中的数据从小到大排序
    public static  void sort(Comparable[] source) {
        //构建堆
        Comparable[] heap = new Comparable[source.length+1];
        createHeap(source,heap);
        //定义一个变量，记录未排序的元素中最大的索引
        int N = heap.length-1;
        //通过循环，交换1索引处的元素和排序的元素中最大的索引处的元素
        while(N!=1){
            //交换元素
            exch(heap,1,N);
            //排序交换后最大元素所在的索引，让它不要参与堆的下沉调整
            N--;
            //需要对索引1处的元素进行对的下沉调整
            sink(heap,1, N);
        }

        //把heap中的数据复制到原数组source中
        System.arraycopy(heap,1,source,0,source.length);

    }


    //在heap堆中，对target处的元素做下沉，范围是0~range
    private static void sink(Comparable[] heap, int target, int range){

        while(2*target<=range){
            //1.找出当前结点的较大的子结点
            int max;
            if (2*target+1<=range){
                if (less(heap,2*target,2*target+1)){
                    max = 2*target+1;
                }else{
                    max = 2*target;
                }
            }else{
                max = 2*target;
            }

            //2.比较当前结点的值和较大子结点的值
            if (!less(heap,target,max)){
                break;
            }

            exch(heap,target,max);

            target = max;
        }
    }

}

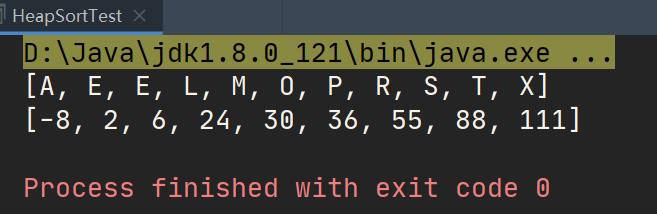
测试:

public class HeapSortTest {

    public static void main(String[] args) {
        // //待排序数组
        String[] arr = {"S","O","R","T","E","X","A","M","P","L","E"};
        Integer[] arr1={2,55,6,-8,36,24,111,88,30};

        //通过HeapSort对数组中的元素进行排序
        HeapSort.sort(arr);
        HeapSort.sort(arr1);
        //打印排序后数组中的元素
        System.out.println(Arrays.toString(arr));
        System.out.println(Arrays.toString(arr1));
    }
}