7.2堆排序的代码分析（算法基础—排序算法）

Posted 2021-12-07 林坤鹏kplin

上一篇：7.1、堆排序的逻辑分析（算法基础—排序算法）

经过上一篇逻辑分析，我们已经知道了堆排序的核心就是解决2个问题：
1、堆的一次向下调整
2、构建堆

但是如果我们仔细看下图，会发现，其实构建堆的过程，就是多次完成“堆的一次向下调整”，只不过这个过程中，要按什么顺序去先后调整各个子树，是个需要考虑的问题。

一、构造堆应该以什么顺序去调整子树

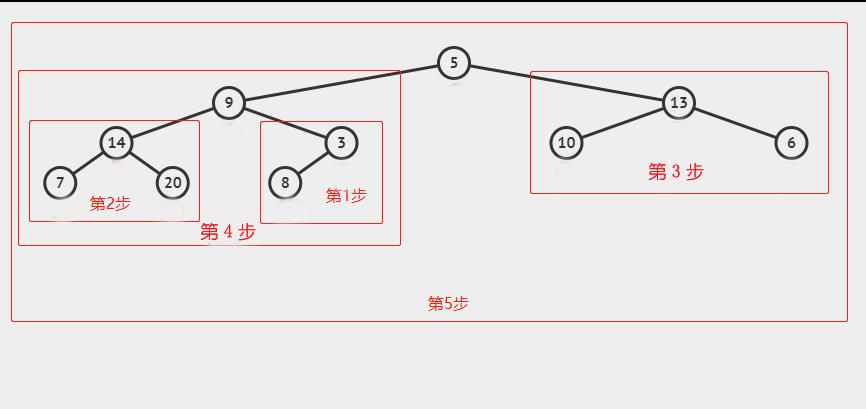
我们直接看每一步需要调整的子树的根节点：

第一步的根节点：3
第二步的根节点：14
第三步的根节点：13
第四步的根节点：9
第五步的根节点：5

上面这个树结构用列表来存储其实就是：

 li = [5, 9, 13, 14, 3, 10, 6, 7, 20, 8]

看看这些根节点在列表中的位置：

其实就是元素3前面的部分，从3的位置开始逆序扫描列表，步长为1，即可找出这些根节点的位置。

目前我们只知道最后一个叶子结点的位置是 len(li) - 1，也就是列表的长度减去1。

而根据前面我们总结的规律是：

1、当父节点的位置为 i 时，它的左孩子节点位置为：2*i+1， 
它的右孩子节点的位置为：2*i+2；

2、当子节点的位置为 i 时，它的父节点的位置为： (i-1)//2

那最后一个叶子结点的父节点3的位置
其实就是 （len(li)-1-1）//2， 等同于 len(li)//2-1

所以我们可以找到最后一个非叶子节点的位置，再层层往上推，找到各个子树的根节点位置，按这顺序对每颗子树都进行一次向下调整，就造堆成功了。

接着拿掉最大值，把最大值放进一个新列表，把最后一个叶子节点的拿到堆顶，又进行一次向下调整，重新得到一个堆，继续把最大值拿掉，把最大值追加到列表…

重复这个过程。最后出来的列表就是一个排好序的列表了。

一个小优化：

上面我们是用一个新列表来存放最大值的，但为了节省空间，我们可以把最大值直接放在原来那列表的最后，并且标识下一次排序时，这个值不参与，最后出来的列表也同样是排好序的，并且不需要另外开个列表占用存储空间。

二、一次向下调整函数怎么写？

我们先拿一个符合条件的图来演示一下：

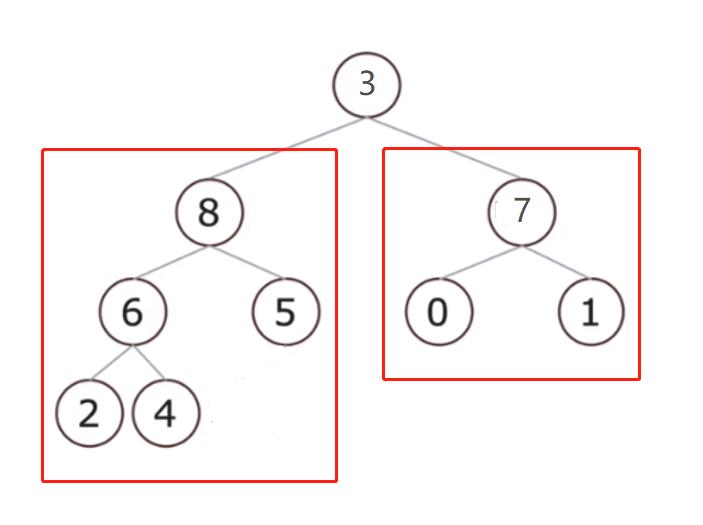
这个图，堆顶不是最大值，但堆顶的左右两个子树，都符合堆的条件（父节点都比孩子节点大），所以我们可以通过一次调整，让堆顶的3回到它应该待的位置去，并且把最大值推选上来。

这个二叉树对应存放到列表应当是：

[3, 8, 7, 6, 5, 0, 1, 2, 4]

1、确认函数所需的参数

我们对这个二叉树做一次向下调整其实就是在调整这个列表中元素的位置。
首先需要把列表传进函数；
其次，我们要拿堆顶出来，把它放到合适的位置，所以也要知道堆顶的位置；
最后因为我们后面会不断把最大值放到这个列表的最后，但这些值又不让它们再次参与排序，所以我们需要有个参数来标识这个列表参与排序的最后一个元素的位置（其实就是用这个参数来逻辑标识等待排序的元素）

所以这个函数必须至少有三个参数：列表li，堆顶位置top，参与排序的最后一个元素的位置last

2、一次向下调整函数代码+逻辑简析

# 向下调整函数
def sift(li, top, last):
    i = top     # i 代表堆顶的位置
    j = 2 * i + 1   # j 代表堆顶的左孩子
    tmp = li[i]
    while j <= last:   # 只要j的位置有数，就一直循环，确保不越界
        if j < last and li[j] < li[j + 1]:   # 如果右孩子比较大，就让j指向右孩子
            j += 1
        if tmp < li[j]:
            li[i] = li[j]     # 上面已经是从左右2个孩子比较后，让j指向更大的孩子了，这里就把更大的孩子放到原来tmp的位置
            i = j           # 把更大的值推选上去了，接下来让i指向刚刚推选上去那个值的位置，也就是向下探一层，再次寻找比tmp更大的值
            j = 2 * i + 1   # j同时也要开始往下一层走
        else:         # 通过上面的循环对比之后，发现tmp已经是比较大的了，就把它放在i的位置
            li[i] = tmp
            break
    li[i] = tmp   #  上面跳出循环的原因也有可能是j超出了位置，没有j可以跟tmp对比了，此时跳出循环，需要再次把tmp放到i位置

# 测试一次向下调整
li = [3, 8, 7, 6, 5, 0, 1, 2, 4]
print('调整前：%s'%li)
sift(li, 0, len(li))
print('调整后：%s'%li)
 

测试结果：

调整后的列表是符合预期的，如下图所示，调整后的二叉树能符合堆的性质

三、堆排序主函数代码+逻辑简析

完成最关键的一次向下调整函数后，我们就可以利用它来构造堆，并且多次调整，完成堆排序了。

针对以下代码解释一下：
1、i 代表堆顶的位置；
2、range(n//2-1, -1, -1)的第一个参数 n//2-1 是最后一个非叶子节点的位置，第二个参数-1是让这个序列倒着遍历，最后一个参数-1是指定步长，也就是向前移动1位。
这样我们就能实现从最后一个非叶子节点的位置开始遍历，每遍历一次可以获取到一个子树的堆顶位置。

def heap_sort(li):
    n = len(li)
    # 开始建堆，i代表堆顶的位置
    for i in range(n//2-1, -1, -1):
        sift(li, i, n- 1)    # 建堆完成
    # 开始向下调整并逐一获取最大值，放到列表最后
    for i in range(n-1, -1, -1):
        li[0], li[i] = li[i], li[0]    # 先把堆顶的最大值和最后一个叶子结点调换位置，接着进行向下调整
        sift(li, 0, i - 1)     # 由于我们把最后一个结点的位置不断往前移，代表这个二叉树是一直在缩小的，
        # 这个过程是为了排除掉那些由堆顶拎出来的最大值，不让它们再继续参与堆的向下调整过程

# 测试堆排序
import random

li = list(range(100))
random.shuffle(li)
print('排序前：%s'%li)
heap_sort(li)
print('排序后：%s'%li)

测试堆排序需要一个打乱的序列，可以使用random.shuffle(li)来打乱
li的顺序。

四、完整代码

# 向下调整函数
def sift(li, top, last):
    i = top     # i 代表堆顶的位置
    j = 2 * i + 1   # j 代表堆顶的左孩子
    tmp = li[i]
    while j <= last:   
        if j < last and li[j] < li[j + 1]:   
            j += 1
        if tmp < li[j]:
            li[i] = li[j]     
            i = j           
            j = 2 * i + 1   
        else:
            li[i] = tmp
            break
    li[i] = tmp
    
def heap_sort(li):
    n = len(li)
    # 开始建堆
    for i in range(n // 2 - 1, -1, -1):
        sift(li, i, n- 1)    # 建堆完成
    # 开始向下调整并逐一出数
    for i in range(n - 1, -1, -1):
        li[0], li[i] = li[i], li[0]
        sift(li, 0, i - 1) 
import random

li = list(range(100))
random.shuffle(li)
print('排序前：%s'%li)
heap_sort(li)
print('排序后：%s'%li)