简单选择排序和堆排序

Posted 2021-05-29 小鹿可可乐

简单选择排序和堆排序

• 1.简单选择排序
• • 1.1排序思想
  • 1.2排序过程图解
  • 1.3代码实现
• 2.堆排序
• • 2.1堆的理解
  • 2.2排序过程图解
  • 2.3代码实现

1.简单选择排序

1.1排序思想

选择排序：每次从待排序队列中找到最小值，和待排序队列的第一位交换即可

在每次遍历过程中，用一个变量保存最小值（minindex）的下标，在遇到更小值时候，替换这个下标，在一趟比较结束后，交换该下标上的值和未排序序列的第一个值（已排序序列的末尾），即把最小值交换过去。
时间复杂度O（n^2）
空间复杂度O（1）
不稳定的

1.2排序过程图解

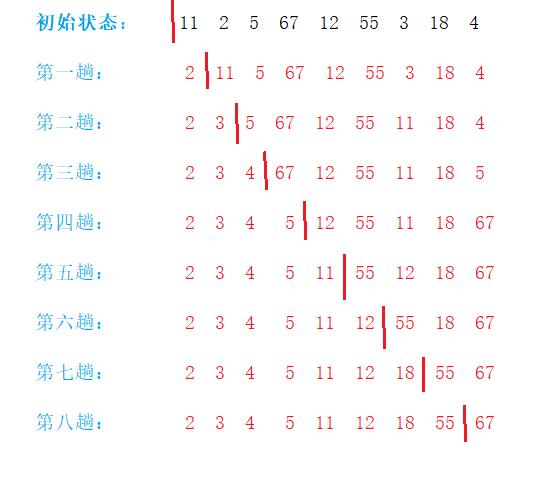
前面是已排序好的，后面是待排序部分

1.3代码实现

//时间复杂度O（n^2） 空间复杂度O（1） 不稳定的
void SelectSort(int arr[], int len)
{
	//assert
	assert(arr != NULL);
	if (NULL == arr)
		return;
		
	int minindex;//存放最小值的下标
	for (int i = 0; i < len - 1; i++)
	{
		minindex = i;//循环开始前先认为待排序队列的第一个值是最小值
		for (int j = i + 1; j<len; j++)
		{
			if (arr[minindex] > arr[j])
			{
				minindex = j;
			}
		}
		if (minindex != i)//这个if判断可以省略，不影响
		{
			int tmp = arr[minindex];
			arr[minindex] = arr[i];
			arr[i] = tmp;
		}
	}
}

2.堆排序

2.1堆的理解

• 堆分为两种：大顶堆和小顶堆，两个统称为堆
  大顶堆：一个二叉树，父节点大于子节点
  小顶堆：一个二叉树，父节点的值小于子节点
  大顶堆和小顶堆的关系：和兄弟节点的值无关，只和父子结点有关

• 什么是树形结构：二叉树，深度，叶子结点，左孩子，右孩子，完全二叉树，满二叉树

• 深度怎么求：logn+1(几叉树就以谁为底，n是数据个数)

• 时间复杂度O（logn）

• 空间 复杂度O（1）

• 不稳定

2.2排序过程图解

调整3个要点：

• 从最后一个非叶子节点子树开始从后向前调整
• 调整的时候顺序是从上向下
• 升序(大顶堆)，降序（小顶堆）
  

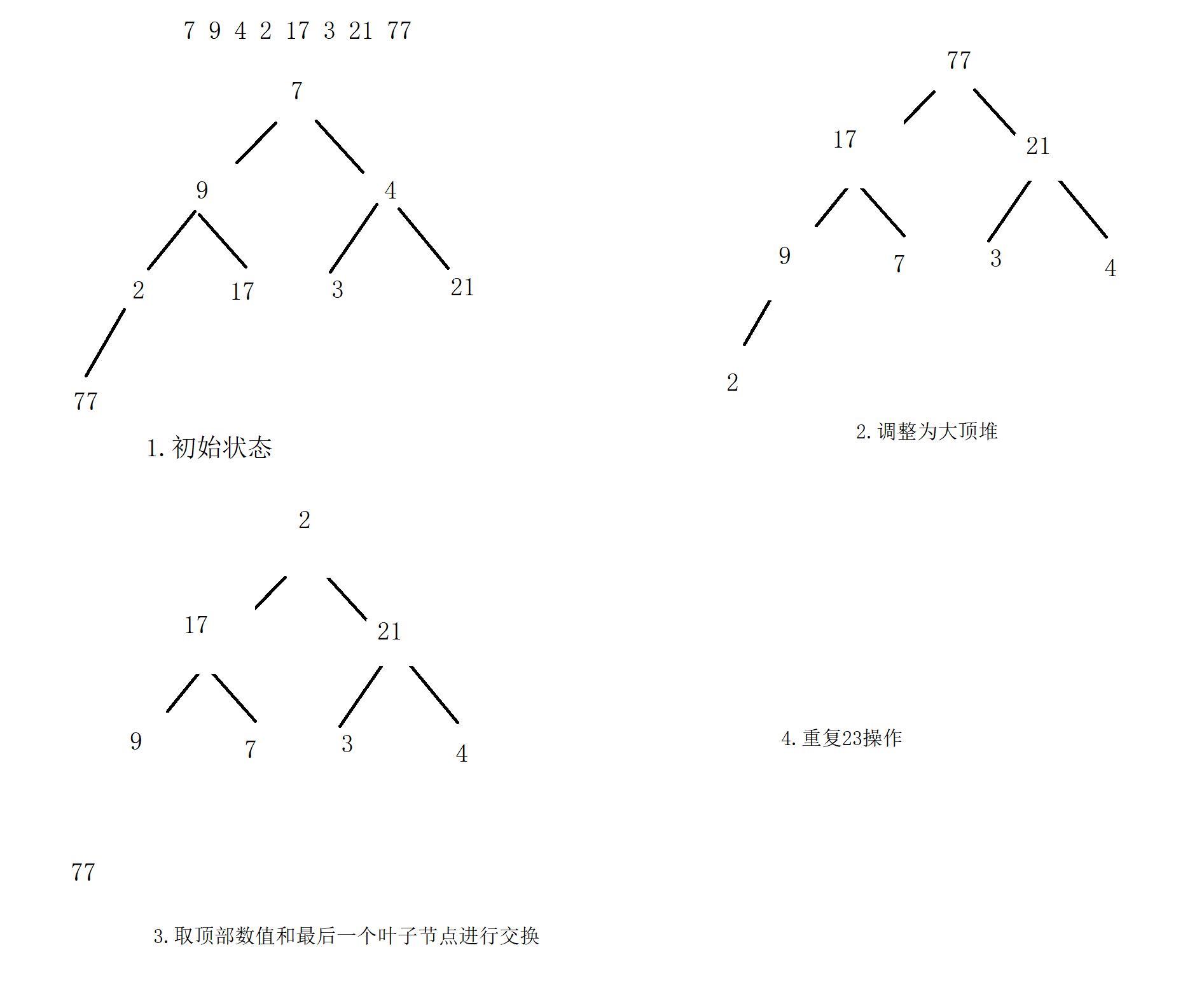
下标规律：

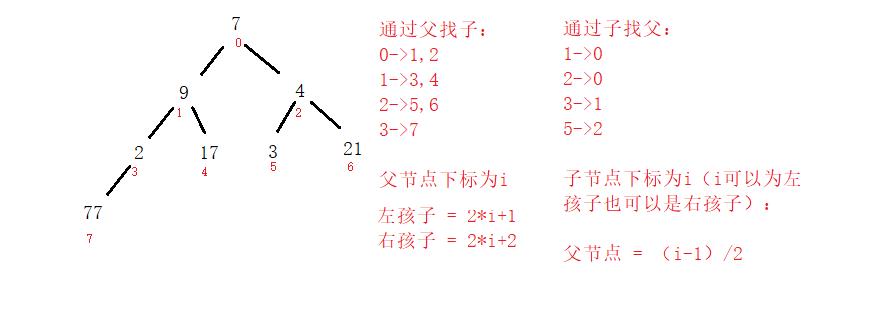
2.3代码实现

static void HeapAdjust(int arr[], int start, int end)

{ 
	int tmp = arr[start];
	for(int i=2*start+1; i<=end; i=i*2+1)//i? 堆排序效率高体现在这里i=i*2+1 
	{ 
		//1.左右孩子都存在 
		//2.只有左孩子，没有右孩子 
		if(i<end && arr[i] < arr[i+1])//通过i<end保证右孩子存在，且arr[i] <arr[i+1]保证左孩子小于右孩子
		{
			i++;//这时候让i指向较大的右孩子下标
		}
		//if判断失败的话，要么没有右孩子，要么有右孩子但是左孩子比右孩子值大，所以i不需要 改变
		if(arr[i] > tmp)//判断较大孩子节点的值是否比父节点的值大，大的话向上覆盖，不然 就找到了合适位置 
		{ 
			arr[start] = arr[i];
			start = i;
		}
		else 
		{ 
			break;//左右孩子中较大的孩子值小于tmp
		}
	}
	arr[start] = tmp;//有两种情况执行到这一行代码：1.触底 2.找到放tmp的合适位置 
}
//堆排序的时间复杂度O（nlogn） 空间复杂度O（1） 不稳定 
void HeapSort(int arr[], int len)
{
	//assert 
	assert(arr != NULL);
	if (NULL == arr)
		return;
	//2.调整为大顶堆
	for (int i = (len - 1 - 1) / 2; i >= 0; i--)//O（nlogn） 
	{
		HeapAdjust(arr, i, len - 1);//
	}
	//第一个for循环走出来，这时已经为大顶堆了
	int tmp = 0;
	for (int j = 0; j < len - 1; j++)//j指的是循环的次数（顶部数据和最后一个节点交换的次 数）//O（nlogn）
	{
		//3.将顶部数据和最后一个节点进行了交换
		tmp = arr[0];
		arr[0] = arr[len - 1 - j];
		arr[len - 1 - j] = tmp;//已经将顶部数据和最后一个节点进行了交换
		//4.重复2.3操作
		HeapAdjust(arr, 0, (len - 1 - j) - 1);
	}
	
}

今天也要好好学习呀~