数学建模 割平面算法求解整数规划基本原理与编程实现

Posted 2021-09-15 DQ_CODING

基本思想

松弛问题:线性规划
割掉一块全部都是小数的区域(这一部分取不到整数)

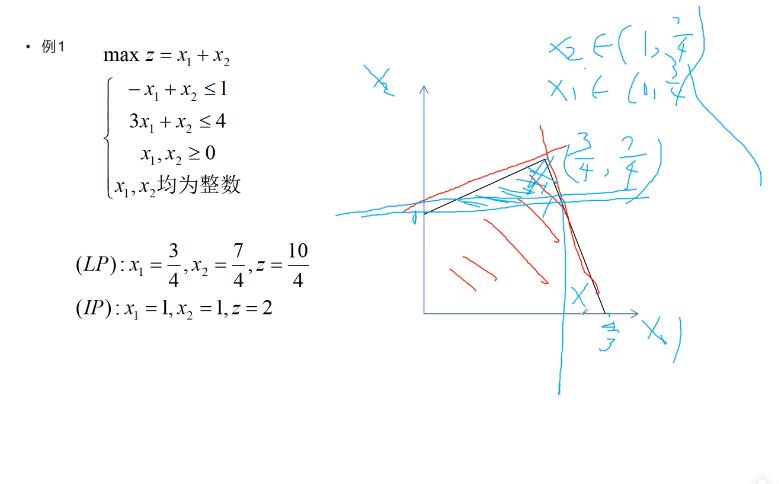
案例

1)横坐标x1,纵坐标x2
2)蓝色小三角形的区域:x2:(1,7/4) x1:(0,3/4)
这块区域,x1与x2完全取不到整数,所以直接切去

所以,此时取值范围变化了:
x2<=1把此约束条件带入,得到x1=1,x2=1,z=2

3)能够取到整数的区域就不能切掉

引入松弛变量:(解出x1=1,x2=1,z=2的过程)
1)松弛变量:引入之后的效果与原先是一致的
如:-x1+x2<=1 引入x3>=0之后 得到 -x1+x2+x3=1 则此时-x1+x2仍然<=1,所以不影响结果

2)把式子4与5的系数与单个数字拆分为(整数+小数,小数>=0)
即:x1=(1+0)x1 -1/4x3=(-1+3/4)x3 1/4x4=(0+1/4)x4 3/4=(0+3/4)

然后再把整数部分(系数为整数与单个整数)放在左边,小数部分放在右边(系数为小数+单个小数)

所以现在变为了
3/4-正数=一个整数
而且0=<3/4<=1 x3,x4>=0
所以 ,3/4-正数<=0
即 3x3+x4>=3
4x2+3x3+x4>=7

基本步骤

引入松弛变量,变不等式为等式
aikxk 松弛变量
aik=[aik]+fik 松弛变量的系数化为正数部分和小数部分
[aik] xk正数部分汇合
fik xk小数部分汇合

[aik]xk -[bi]整数部分放在左侧
[bi]+fi 小数部分放在右侧

切割平面法流程

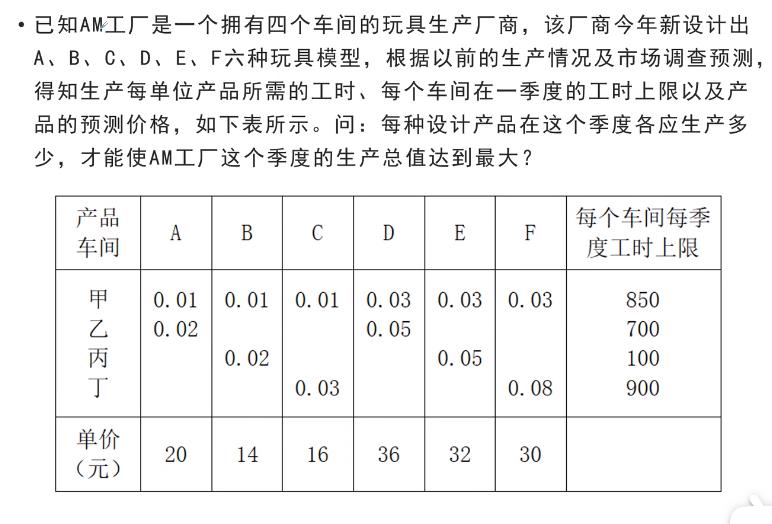
案例

解答:

引入松弛变量:
matlab中只有min,所以求最大值要加上负号

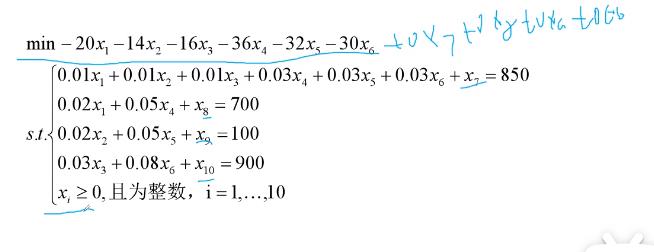
matlab代码

DividePlane.m

function  [intx,intf] = DividePlane(A,c,b,baseVector)
%功能：用割平面法求解整数规划
%调用格式：[intx,intf]=DividePlane(A,c,b,baseVector)
%其中，A：约束矩阵；
%      c：目标函数系数向量；
%      b：约束右端向量；
%      baseVector：初始基向量；
%      intx：目标函数取最小值时的自变量值；
%      intf：目标函数的最小值；
sz = size(A);
nVia = sz(2);%获取有多少决策变量
n = sz(1);%获取有多少约束条件
xx = 1:nVia;

if length(baseVector) ~= n
    disp('基变量的个数要与约束矩阵的行数相等！');
    mx = NaN;
    mf = NaN;
    return;
end
 
M = 0;
sigma = -[transpose(c) zeros(1,(nVia-length(c)))];
xb = b;
 
%首先用单纯形法求出最优解
while 1   
    [maxs,ind] = max(sigma);
%--------------------用单纯形法求最优解--------------------------------------
    if maxs <= 0   %当检验数均小于0时，求得最优解。      
        vr = find(c~=0 ,1,'last');
        for l=1:vr
            ele = find(baseVector == l,1);
            if(isempty(ele))
                mx(l) = 0;
            else
                mx(l)=xb(ele);
            end
        end
        if max(abs(round(mx) - mx))<1.0e-7  %判断最优解是否为整数解，如果是整数解。
            intx = mx;
            intf = mx*c;
            return;
        else  %如果最优解不是整数解时，构建切割方程
            sz = size(A);
            sr = sz(1);
            sc = sz(2);
            [max_x, index_x] = max(abs(round(mx) - mx));
            [isB, num] = find(index_x == baseVector);
            fi = xb(num) - floor(xb(num));
            for i=1:(index_x-1)
                Atmp(1,i) = A(num,i) - floor(A(num,i));
            end
            for i=(index_x+1):sc
                Atmp(1,i) = A(num,i) - floor(A(num,i));
            end
            
            Atmp(1,index_x) = 0; %构建对偶单纯形法的初始表格
            A = [A zeros(sr,1);-Atmp(1,:) 1];
            xb = [xb;-fi];
            baseVector = [baseVector sc+1];
            sigma = [sigma 0];
         
            %-------------------对偶单纯形法的迭代过程----------------------
            while 1
                %----------------------------------------------------------
                if xb >= 0    %判断如果右端向量均大于0，求得最优解
                    if max(abs(round(xb) - xb))<1.0e-7   %如果用对偶单纯形法求得了整数解，则返回最优整数解
                        vr = find(c~=0 ,1,'last');
                        for l=1:vr
                            ele = find(baseVector == l,1);
                            if(isempty(ele))
                                mx_1(l) = 0;
                            else
                                mx_1(l)=xb(ele);
                            end
                        end
                        intx = mx_1;
                        intf = mx_1*c;
                        return;
                    else   %如果对偶单纯形法求得的最优解不是整数解，继续添加切割方程
                        sz = size(A);
                        sr = sz(1);
                        sc = sz(2);
                        [max_x, index_x] = max(abs(round(mx_1) - mx_1));
                        [isB, num] = find(index_x == baseVector);
                        fi = xb(num) - floor(xb(num));
                        for i=1:(index_x-1)
                            Atmp(1,i) = A(num,i) - floor(A(num,i));
                        end
                        for i=(index_x+1):sc
                            Atmp(1,i) = A(num,i) - floor(A(num,i));
                        end
                        Atmp(1,index_x) = 0;  %下一次对偶单纯形迭代的初始表格
                        A = [A zeros(sr,1);-Atmp(1,:) 1];
                        xb = [xb;-fi];
                        baseVector = [baseVector sc+1];
                        sigma = [sigma 0];
                        continue;
                    end
                else   %如果右端向量不全大于0，则进行对偶单纯形法的换基变量过程
                    minb_1 = inf;
                    chagB_1 = inf;
                    sA = size(A);
                    [br,idb] = min(xb);
                    for j=1:sA(2)
                        if A(idb,j)<0
                            bm = sigma(j)/A(idb,j);
                            if bm<minb_1
                                minb_1 = bm;
                                chagB_1 = j;
                            end
                        end
                    end
                    sigma = sigma -A(idb,:)*minb_1;
                    xb(idb) = xb(idb)/A(idb,chagB_1);
                    A(idb,:) = A(idb,:)/A(idb,chagB_1);
                    for i =1:sA(1)
                        if i ~= idb
                            xb(i) = xb(i)-A(i,chagB_1)*xb(idb);
                            A(i,:) = A(i,:) - A(i,chagB_1)*A(idb,:);
                        end
                    end
                    baseVector(idb) = chagB_1;
                end
              %------------------------------------------------------------
            end 
            %--------------------对偶单纯形法的迭代过程---------------------    
        end     
    else     %如果检验数有不小于0的，则进行单纯形算法的迭代过程
        minb = inf;
        chagB = inf;
        for j=1:n
            if A(j,ind)>0
                bz = xb(j)/A(j,ind);
                if bz<minb
                    minb = bz;
                    chagB = j;
                end
            end
        end
        sigma = sigma -A(chagB,:)*maxs/A(chagB,ind);
        xb(chagB) = xb(chagB)/A(chagB,ind);
        A(chagB,:) = A(chagB,:)/A(chagB,ind);
        for i =1:n
            if i ~= chagB
                xb(i) = xb(i)-A(i,ind)*xb(chagB);
                A(i,:) = A(i,:) - A(i,ind)*A(chagB,:);
            end
        end
        baseVector(chagB) = ind;
    end
    M = M + 1;
    if (M == 1000000)
        disp('找不到最优解！');
        mx = NaN; 
        minf = NaN;
        return;
    end
end