如何用MATLAB求解0-1整数规划?

Posted 2023-05-09

bintprog 求解0-1规划问题 格式如下
x = bintprog(f)
x = bintprog(f, A, b)
x = bintprog(f, A, b, Aeq, beq)
x = bintprog(f, A, b, Aeq, beq, x0)
x = bintprog(f, A, b, Aeq, Beq, x0, options)
[x, fval] = bintprog(...)
[x,fval, exitflag] = bintprog(...)
[x, fval, exitflag, output] = bintprog(...)

这里x是问题的解向量
f是由目标函数的系数构成的向量
A是一个矩阵，b是一个向量
A，b和变量x=x1,x2,…,xn一起，表示了线性规划中不等式约束条件
A，b是系数矩阵和右端向量。
Aeq和Beq表示了线性规划中等式约束条件中的系数矩阵和右端向量。
X0是给定的变量的初始值
options为控制规划过程的参数系列。
返回值中fval是优化结束后得到的目标函数值。
exitflag=0表示优化结果已经超过了函数的估计值或者已声明的最大迭代次数；
exitflag>0表示优化过程中变量收敛于解X，
exitflag<0表示计算不收敛。
output有3个分量，
iterations表示优化过程的迭代次数，
cgiterations表示PCG迭代次数，
algorithm表示优化所采用的运算规则。
在使用linprog()命令时，系统默认它的参数至少为1个，
但如果我们需要给定第6个参数，则第2、3、4、5个参数也必须给出，否则系统无法认定给出的是第6个参数。遇到无法给出时，则用空矩阵“[]”替代。

例如

max=193*x1+191*x2+187*x3+186*x4+180*x5+185*x6; %f由这里给出

st.
x5+x6>=1;
x3+x5>=1;
x1+x2<=1;
x2+x6<=1;
x4+x6<=1;
%a、b由不等关系给出，如没有不等关系，a、b取[]

x1+x2+x3+x4+x5+x6=1; %aep、bep由等式约束给出

代码如下
f=[-193;-191;-187;-186;-180;-185;];
a=[0 0 0 0 -1 -1;0 -1 0 0 -1 0;1 1 0 0 0 0;0 1 0 0 0 1;0 0 0 1 0 1];
b=[-1,-1,1,1,1]';
aeq=[1 1 1 1 1 1];
beq=[3];
x=bintprog(f,a,b,aeq,beq)

注意
目标值为最大值时应乘以-1化为求最小值；
不等约束为>=时应乘以-1化为<=; 参考技术A 用lingo，好用，专门做优化的，比matlab好用，matlab得到的可能不是全局最优解

如何用matlab求解微分方程并画图

Dy/Dx=ycos(x)/(1+2y^2),y(0)=1
这道题怎么用matlab求解并画出图啊

1、找到关于求解常微分方程的习题。

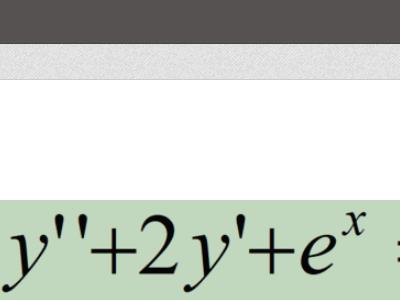
2、这里用matlab求解，主要用到的就是“dsolve”，具体的格式如下，但是不仅仅局限下面两种，其中eq就是代表方程式，而con为初始条件。

3、这里的“x”关于x的函数。知道语法就可以进行计算了。

4、在matlab中输入如下，dsolve('D2y+2*Dy+exp(x)=0','x')，并直接回车就可以显示计算结果了。

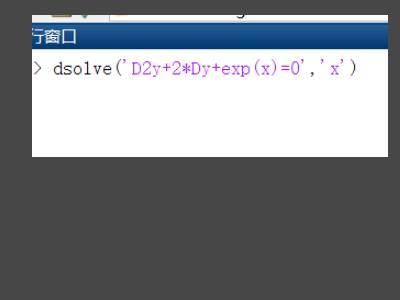
5、框中为最终求解的通解。

参考技术A

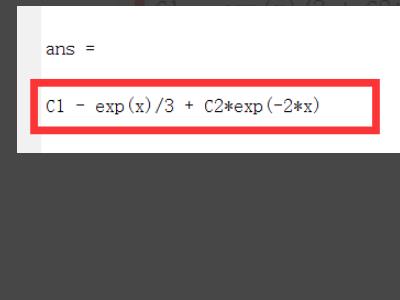
由于方程比较复杂，解析解不能用初等函数表示

只是要获得图像的话，用数值计算的办法可能更方便

fun=@(t,y) 1.44*(10^9)*(1-y).*exp(-109170./(8.314*t));

[T,Y] = ode23t(fun,500:600,0);

DY=fun(T,Y);

AX=plotyy(T,Y,T,DY);

set(get(AX(1),'Xlabel'),'String','T');

set(get(AX(1),'Ylabel'),'String','\\alpha');

set(get(AX(2),'Ylabel'),'String','d\\alpha/dT');

T是自变量，Y是变量也就是alpha

DY是，Y对T的导数

得到得到结果如下图

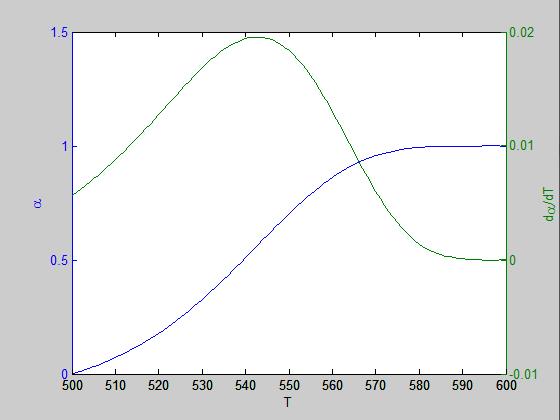
从图像看出，在T=500时，alpha=0

大概在T=600时，d(alpha)/dT趋向于0，alpha趋向于1不变

但是由于是数值解，在T不断增加的时候，d(alpha)/dT会在0附近振荡

所以T的取值不宜取得太大，这里取500到600之间

而采用ode23t函数，减少振荡

实际上，当T增大到一定值的时候，d(alpha)/dT趋向于0，

函数趋向于保持恒定值，所以后续的振荡是不合理的

取一定的区间如上图，已经可以很好地得到函数的变化趋势了

参考技术B

dsolve()求解微分方程后，使用ezplot()作图，参考代码：

>> y = dsolve('Dy=y*cos(x)/(1+2*y^2)','y(0)=1','x');
>> ezplot(y,[-10,10]) % [-10,10]为x区间

追问

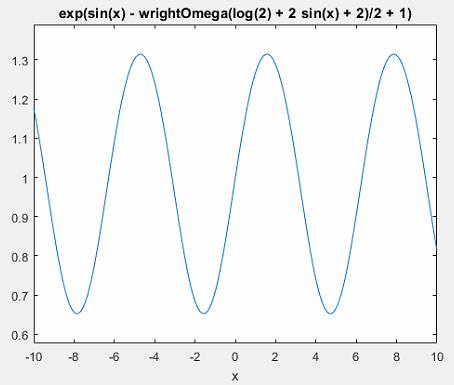
未定义与 'char' 类型的输入参数相对应的函数 'dsolve'。是为什么啊

追答

你是哪个版本的matlab？输入 help dsolve 。看看你的版本使用dsolve()函数的例子

追问

我的是R2014a版本，help找不到dsolve，但是有个fsolve
fsolve Solve system of nonlinear equations
x = fsolve(fun,x0)
x = fsolve(fun,x0,options)
x = fsolve(problem)

追答

不应该啊，我的2010和2015版本都有这个函数，我没装2014版本，所以不知道问题所在了

追问

好吧，谢谢你