备战数学建模19-数学规划问题

Posted 2022-05-17 nuist__NJUPT

目录

一、线性规划

1-线性规划的概念

2-线性规划的实例与定义

3-线性规划MATLAB与lingo实现

4-可转化为线性规划的问题

5-线性规划问题实战案例

二、整数规划

1-整数规划相关概念

2-整数规划相关案例 

3-不同整数规划的介绍

4-整数规划的常见求解方法

5-整数规划求解方法之分支定界算法

6-整数规划求解方法之割平面算法

7-整数规划求解方法之匈牙利算法

三、非线性规划

1-非线性规划的相关概念

2-非线性规划的基本数学模型

3-非线性规划案例

3-二次规划

4-非线性规划经典案例

---

不知不觉 ，准备建模有些时日了，今天开始数学数学规划方面的知识，我要开始开车了，兄弟们站稳扶好，开始发车。

一、线性规划

1-线性规划的概念

2-线性规划的实例与定义

 规划问题：目标变量+决策函数+约束条件

 

3-线性规划MATLAB与lingo实现

对于上面线性规划问题，MATLAB代码如下所示：

clear; clc
f = [-2; -3; 5] ;
a = [-2, 5, -1; 1, 3, 1] ;
b = [-10; 12] ;
aeq = [1,1,1] ;
beq = 7 ;
[x,y] = linprog(f,a,b,aeq,beq,zeros(3,1)) ;
y=-y;
disp(x) ;
disp(y) ;

对于上面线性规划问题，LINGO代码如下所示：

model:
max = 2*x1 + 3*x2 - 5*x3 ;
x1 + x2 + x3 = 7;
2*x1 - 5*x2 + x3 >= 10;
x1 + 3*x2 + x3 <= 12;
end

4-可转化为线性规划的问题

5-线性规划问题实战案例

 ​​

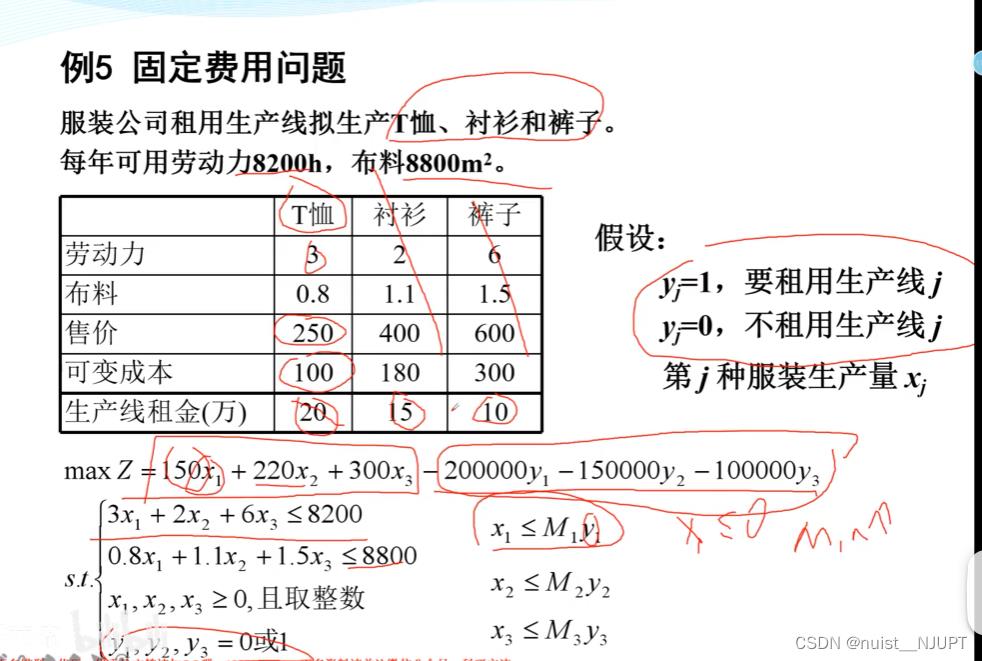
二、整数规划

1-整数规划相关概念

  

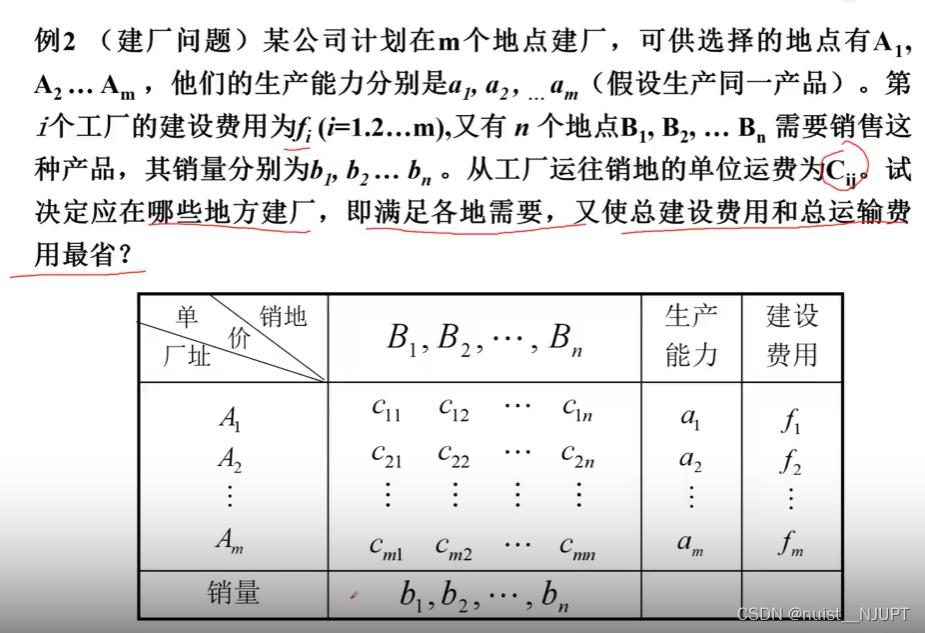
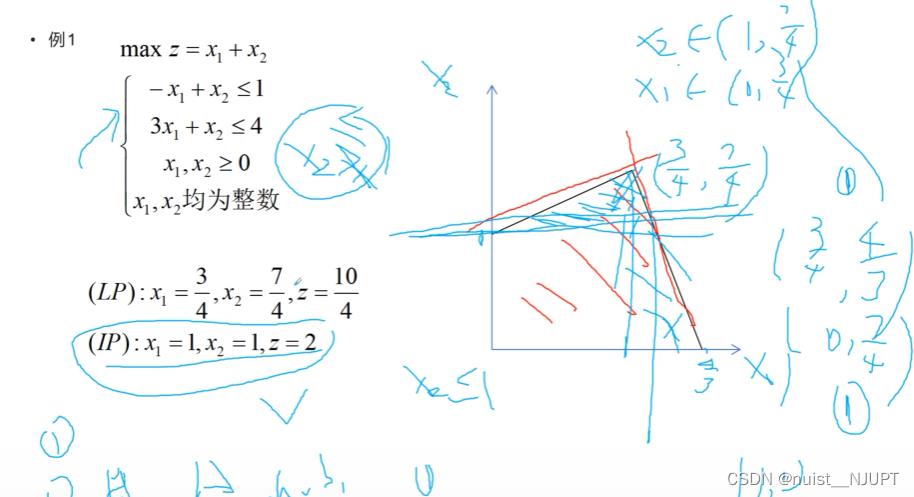
2-整数规划相关案例 

3-不同整数规划的介绍

4-整数规划的常见求解方法

 

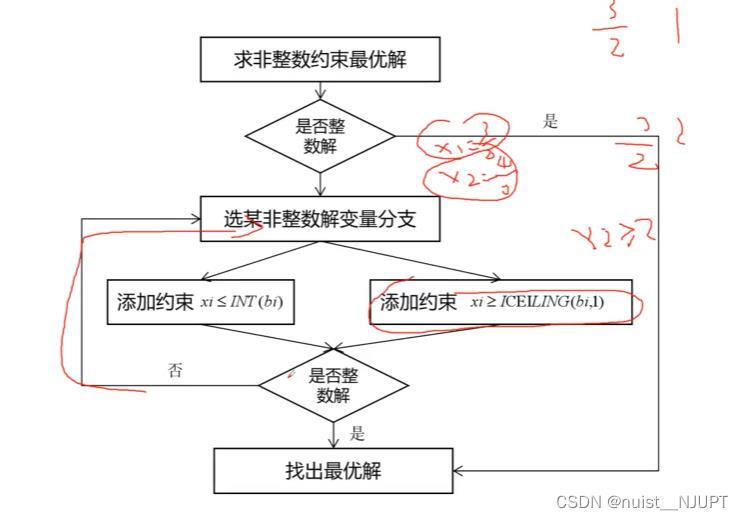
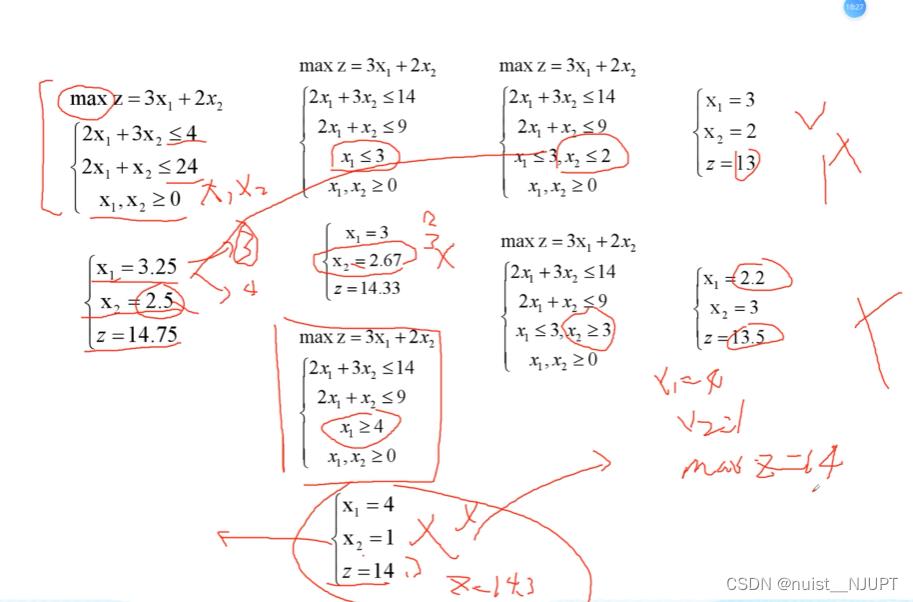
5-整数规划求解方法之分支定界算法

 

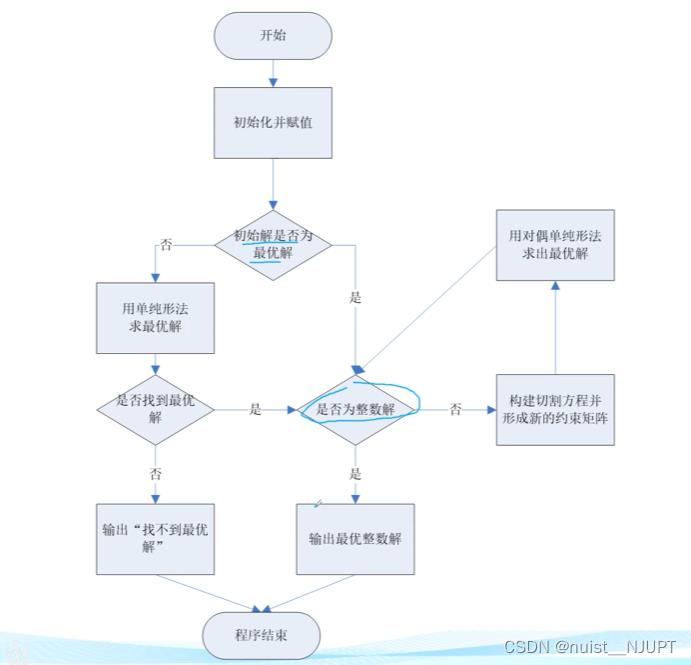
6-整数规划求解方法之割平面算法

 

 

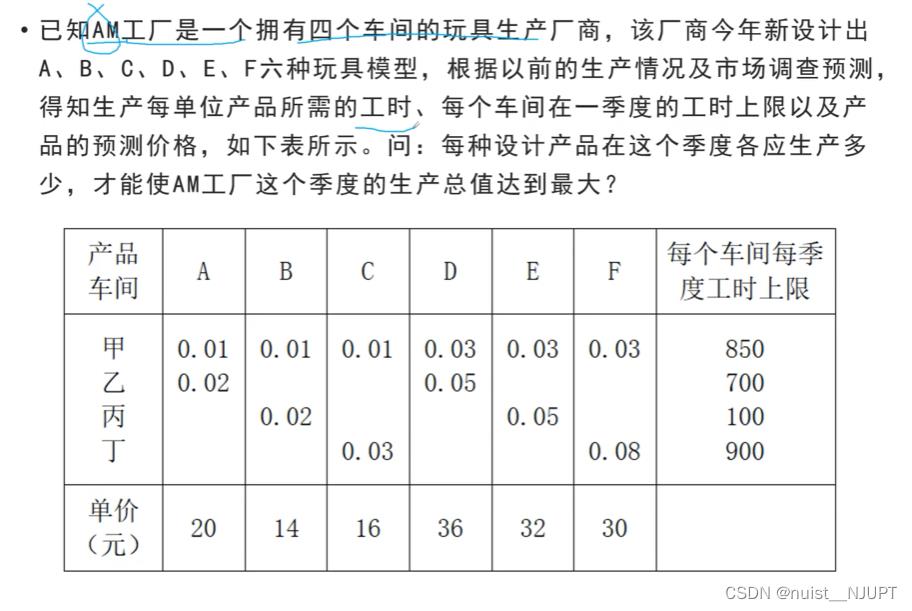
哈哈，其实直接用lingo很方便，用MATLAB还要先松弛，再用算法求解，很麻烦。

lingo代码如下：

model:

max = 20*x1 + 14*x2 + 16*x3 + 36*x4 + 32*x5 + 30*x6;
0.01*x1 + 0.01*x2 + 0.01*x3 + 0.03*x4 + 0.03*x5 + 0.03*x6 <= 850 ;
0.02*x1 + 0.05*x4  <= 700 ;
0.02*x2 + 0.05*x5 <= 100;
0.03*x3 + 0.08*x6 <= 900 ;

@gin(x1) ;
@gin(x2) ;
@gin(x3) ;
@gin(x4) ;
@gin(x5) ;
@gin(x6) ;
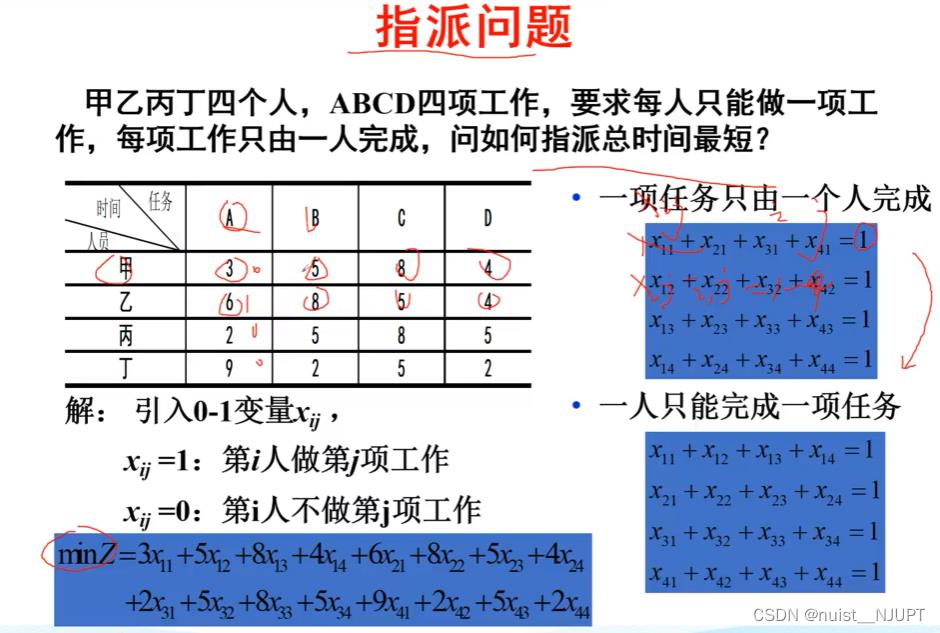
end

7-整数规划求解方法之匈牙利算法

 

 

 

三、非线性规划

1-非线性规划的相关概念

2-非线性规划的基本数学模型

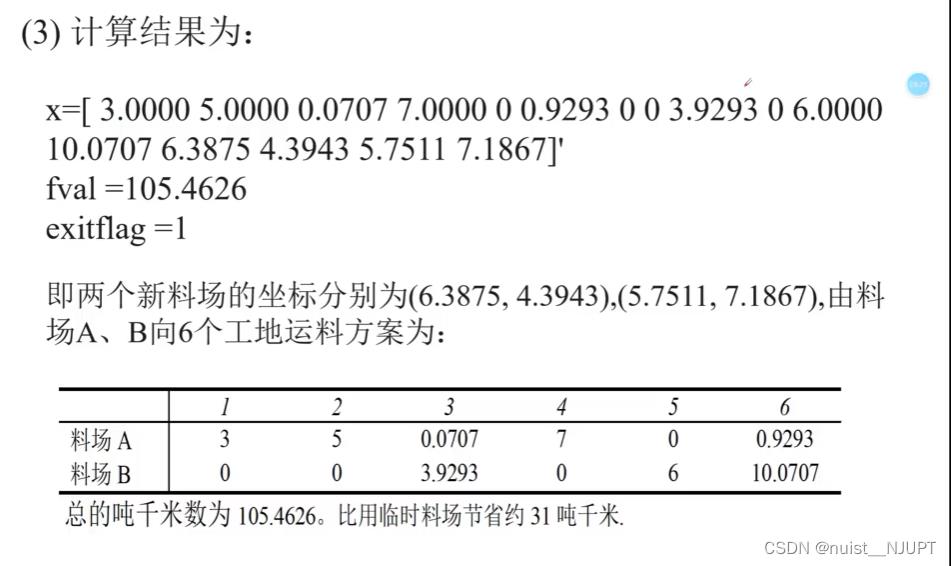
3-非线性规划案例

MATLAB求解上述非线性规划的过程如下所示：

lingo也可以求解，代码如下：

model:
min = x1*x1 + x2*x2 + x3*x3 + 8 ;
x1*x1 - x2 + x3*x3 >= 0 ;
x1 + x2*x2 + x3*x3 <= 20 ;
-x1 -x2*x2 + 2 = 0 ;
x2 + 2*x3*x3 = 3 ;

end

3-二次规划

 

上述二次规划的lingo代码如下：

model:
min = 2*x1*x1 - 4*x1*x2 + 4*x2*x2 - 6*x1 - 3*x2 ;
x1 + x2 <= 3 ;
4*x1 + x2 <= 9 ;

end

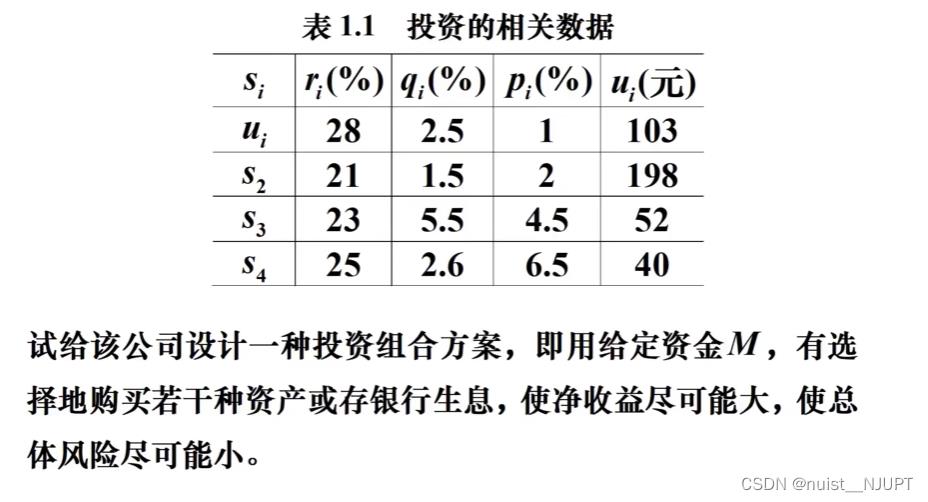
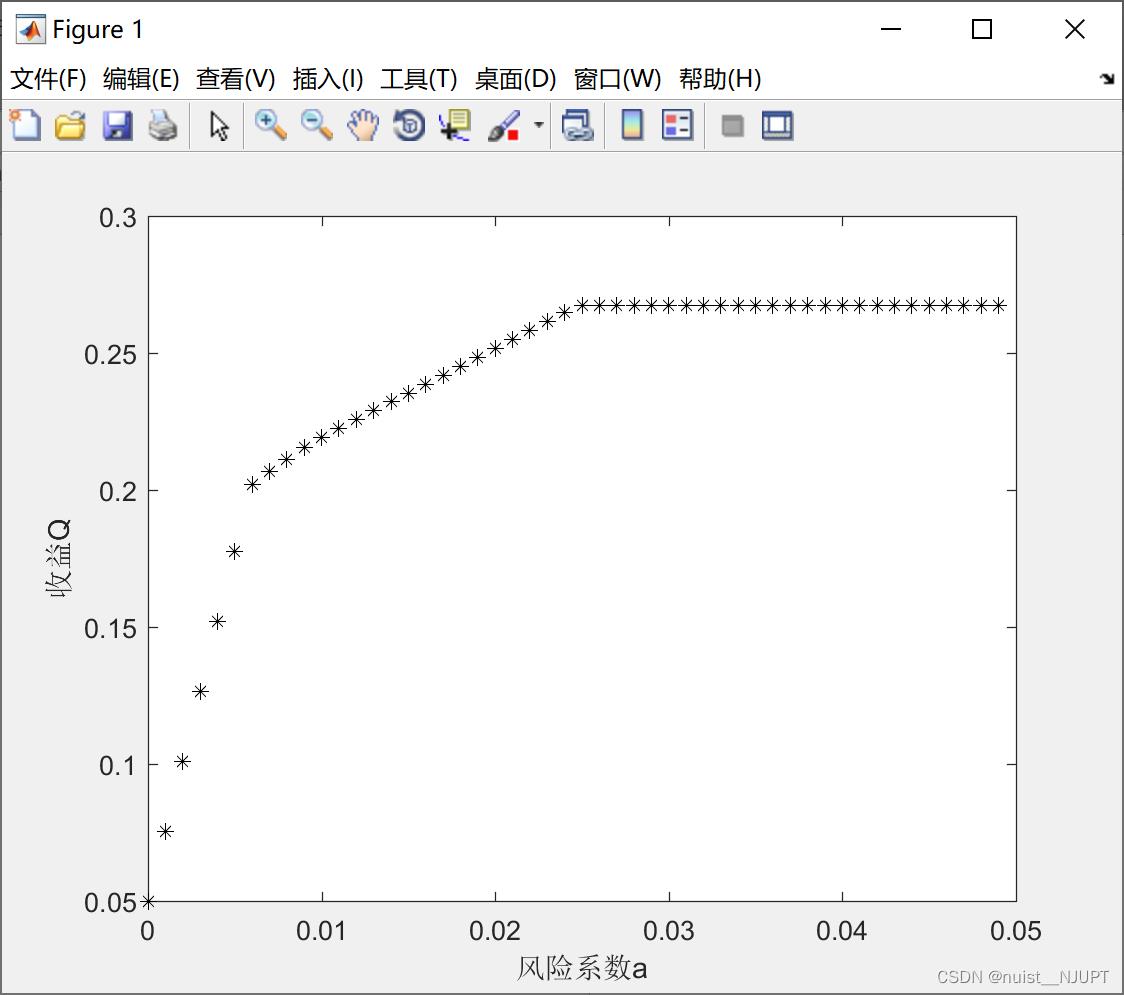
4-非线性规划经典案例