运筹学 整数规划割平面法 题求解
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了运筹学 整数规划割平面法 题求解相关的知识,希望对你有一定的参考价值。
割平面法是1958年由美国学者高莫利(R.E.GoMory)提出的求解全整数规划的一种比较简单的方法。其基本思想和分枝定界法大致相同,即先不考虑变量的取整约束,用单纯形法求解相应的线性规划。
如果所得的最优解为整数解,那么它也是原整数规划问题的最优解3如果最优解不是整数解,那么分枝定界法是任取一个取分数值的变量Xk = bk将原整数规划分成两枝。
其实质是用两个垂直于坐标轴的平行平面Xk = [bk]和Xk = [bk] + 1将原可行域R分成两个可行域R1和R2,并将两个平行平面之间的不含有整数解的那一部分可行域去掉,以缩小可行域。

整数规划又分为:
1、纯整数规划:所有决策变量均要求为整数的整数规划。
2、混合整数规划:部分决策变量均要求为整数的整数规划。
3、纯0-1整数规划:所有决策变量均要求为0-1的整数规划。
4、混合0-1规划:部分决策变量均要求为0-1的整数规划。
参考技术A题主的运筹学问题,可以这样来求解。
第一步,在直角坐标系中,绘制 3*x1+2*x2=7 的直线
第二步,在直角坐标系中,绘制 x1+4*x2=5 的直线
第三步,在直角坐标系中,绘制 3*x1+x2=2 的直线
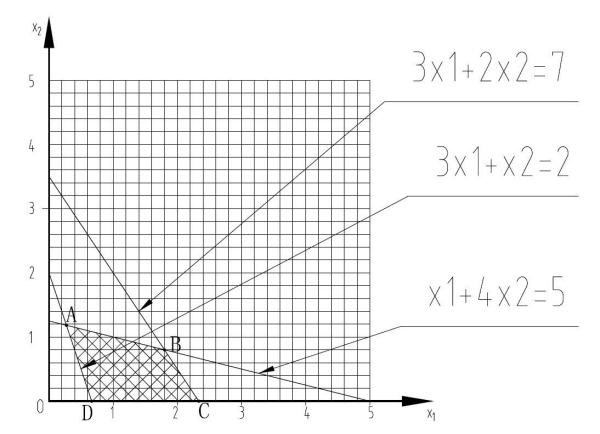
第四步,得到 ABCD 四边形(从上图我们可以得到)
第五步,由于x、y是整数,所以我们可以x=1,y=1
第六步,由此我们得到z的最小值,即
Zmin=4*1+5*1=9
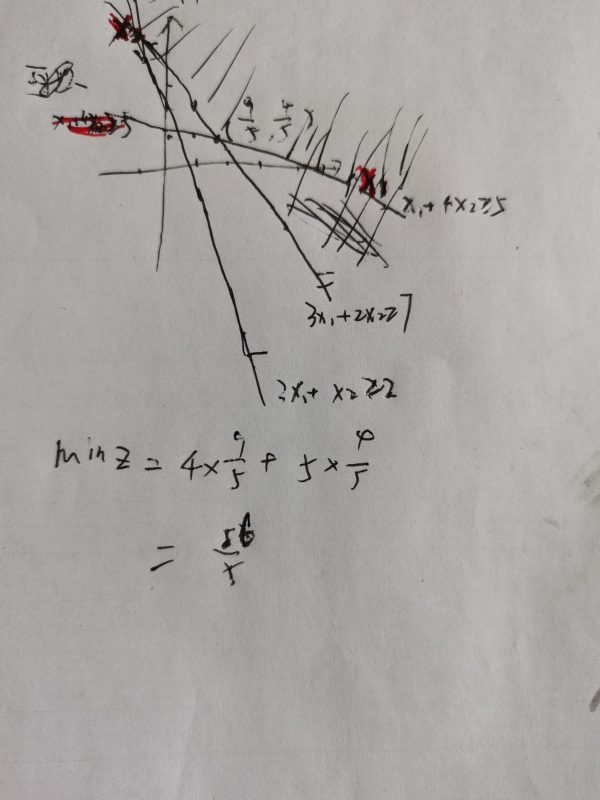
参考技术B如图所示,图画得不好,凑合看,就把x2当成y来看就可以,并不难
望采纳
运筹学整数规划 ( 整数规划求解方法 | 指派问题 )
文章目录
一、整数规划求解方法
分支定界法 ( 普通整数规划 ) : 主要处理整数规划问题 , 规划中的变量要求是整数 ;
匈牙利法 ( 指派问题 ) : 变量只能取 0 , 1 0 , 1 0,1 值的整数规划 , 如果有 n n n 个变量 , 则一共可能有 2 n 2^n 2n 种可能的取值 , 使用穷举法可能比较简单 ; 在进一步 , 将一些条件考虑进其中 , 可以排除掉一些取值 , 使得搜索范围变小 ;
二、指派问题
指派问题 : 给 4 4 4 个人指派 4 4 4 个岗位 , 每个人在不同的岗位产生的利润不同 , 如何安排使得利润最高 ;
| A A A | B B B | C C C | D D D | |
|---|---|---|---|---|
| 甲 | 85 85 85 | 92 92 92 | 73 73 73 | 90 90 90 |
| 乙 | 95 95 95 | 87 87 87 | 78 78 78 | 95 95 95 |
| 丙 | 82 82 82 | 83 83 83 | 79 79 79 | 90 90 90 |
| 丁 | 86 86 86 | 90 90 90 | 80 80 80 | 88 88 88 |
首先进行 变量选取 , 这里人与工作的关系只是 做 / 不做 工作 , 这里将 甲 是否做 A , B , C , D A , B, C, D A,B,C,D 工作设置为变量分别设置为 x 11 , x 12 , x 13 , x 14 x_11, x_12, x_13, x_14 x11,x12,x13,x14 ,
甲 如果做 A A A 工作 , x 11 = 1 x_11 = 1 x11=1 , 如果不做 A A A 工作 , x 11 = 0 x_11 = 0 x11=0 ;
16 16 16 个变量如下 :
| A A A | B B B | C C C | D D D | |
|---|---|---|---|---|
| 甲 | x 11 x_11 x11 | x 12 x_12 x12 | x 13 x_13 x13 | x 14 x_14 x14 |
| 乙 | x 21 x_21 x21 | x 22 x_22 x22 | x 23 x_23 x23 | x 24 x_24 x24 |
| 丙 | x 31 x_31 x31 | x 32 x_32 x32 | x 33 x_33 x33 | x 34 x_34 x34 |
| 丁 | x 41 x_41 x41 | x 42 x_42 x42 | x 43 x_43 x43 | x 44 x_44 x44 |
目标函数就是总的利润值 , 将两个表格中的元素按位相乘再相加即可 ;
约束条件 ① 每个人只能做一项工作 , 甲的对应 4 4 4 个变量相加之和等于 1 1 1 ; 同理 乙丙丁 对应的 4 4 4 个变量相加之和也等于 1 1 1 ;
约束条件 ② 每个工作只能指派一个人 , A A A 的对应 4 4 4 个变量相加之和等于 1 1 1 ; 同理 B C D BCD BCD 对应的 4 4 4 个变量相加之和也等于 1 1 1 ;
上述指派问题数学模型 :
m
a
x
Z
=
85
x
11
+
92
x
12
+
73
x
13
+
90
x
14
+
95
x
21
+
87
x
22
+
78
x
23
+
95
x
24
+
82
x
31
+
83
x
32
+
79
x
33
+
90
x
34
+
86
x
41
+
90
x
42
+
80
x
43
+
88
x
44
s
.
t
x
11
+
x
12
+
x
13
+
x
14
=
1
x
21
+
x
22
+
x
23
+
x
24
=
1
x
31
+
x
32
+
x
33
+
x
34
=
1
x
41
+
x
42
+
x
43
+
x
44
=
1
x
11
+
x
21
+
x
31
+
x
41
=
1
x
12
+
x
22
+
x
32
+
x
42
=
1
x
13
+
x
23
+
x
33
+
x
43
=
1
x
14
+
x
24
+
x
34
+
x
44
=
1
x
i
j
=
0
,
1
(
i
,
j
=
1
,
2
,
3
,
4
)
\\beginarraylcl \\rm maxZ = 85x_11 + 92x_12 + 73x_13 + 90x_14 + \\\\ \\rm \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ 95x_21 + 87x_22 + 78x_23 + 95x_24 + \\\\ \\rm \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ 82x_31 + 83x_32 + 79x_33 + 90x_34 + \\\\ \\rm \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ 86x_41 + 90x_42 + 80x_43 + 88x_44 \\\\\\\\ \\rm s.t\\begincases \\rm x_11 + x_12 + x_13 + x_14 = 1 \\\\ \\rm x_21 + x_22 + x_23 + x_24 = 1 \\\\ \\rm x_31 + x_32 + x_33 + x_34 = 1 \\\\ \\rm x_41 + x_42 + x_43 + x_44 = 1 \\\\\\\\ \\rm x_11 + x_21 + x_31 + x_41 = 1 \\\\ \\rm x_12 + x_22 + x_32 + x_42 = 1 \\\\ \\rm x_13 + x_23 + x_33 + x_43 = 1 \\\\ \\rm x_14 + x_24 + x_34 + x_44 = 1 \\\\\\\\ \\rm x_ij = 0 , 1 \\ \\ \\ \\ (i , j= 1,2,3,4 ) \\endcases\\endarray
maxZ=85x11+92x12+73x13+90x14+ 95x21+87x< 以上是关于运筹学 整数规划割平面法 题求解的主要内容,如果未能解决你的问题,请参考以下文章