用matlab求解整数规划双角标问题

Posted 2023-05-10

参考技术A 详情见下。
运筹学理论上，如不加特殊说明，一般指整数线性规划。对于整数线性规划模型大致可分为两类：
1、变量全限制为整数时，称纯（完全）整数规划。
2、变量部分限制为整数的，称混合整数规划。
理论求解方法分类：
（i）分枝定界法—可求纯或混合整数线性规划。
（ii）割平面法—可求纯或混合整数线性规划。
（iii）隐枚举法—求解“0-1”整数规划：①过滤隐枚举法；②分枝隐枚举法。
（iv）匈牙利法—解决指派问题（“0-1”规划特殊情形）。
（v）蒙特卡洛法—求解各种类型规划。
整数线性规划可以用linprog函数，help里有超级详细的说明，0-1整数规划可以用bintprog函数。

路径规划基于matlab麻雀算法求解机器人栅格地图最短路径规划问题含Matlab源码 1582期

一、简介

路径规划是实现移动机器人自主导航的关键技术，是指在有障碍物的环境中，按照一定的评价标准（如距离、时间、能耗等），寻找到一条从起始点到目标点的无碰撞路径，这里选取最短距离路径规划的评价标准，即最短路径规划问题。

1．路径规划数学模型的建立
将移动机器人周围环境用一组数据进行抽象表达，建立二维或三维的环境模型，得到移动机器人能够理解分析的环境数据，是机器人路径规划的基本前提。我这里用的是栅格法，其原理是将周围环境看成一个二维平面，将平面分成一个个等面积大小的具有二值信息的栅格，每个栅格中存储着周围环境信息量，下图我给出了一个栅格法地图，方便大家更好的理解栅格地图。这里设计的栅格地图为一个20×20的地形矩阵，黑色的地方表示有障碍，白色的地方表示没有障碍。

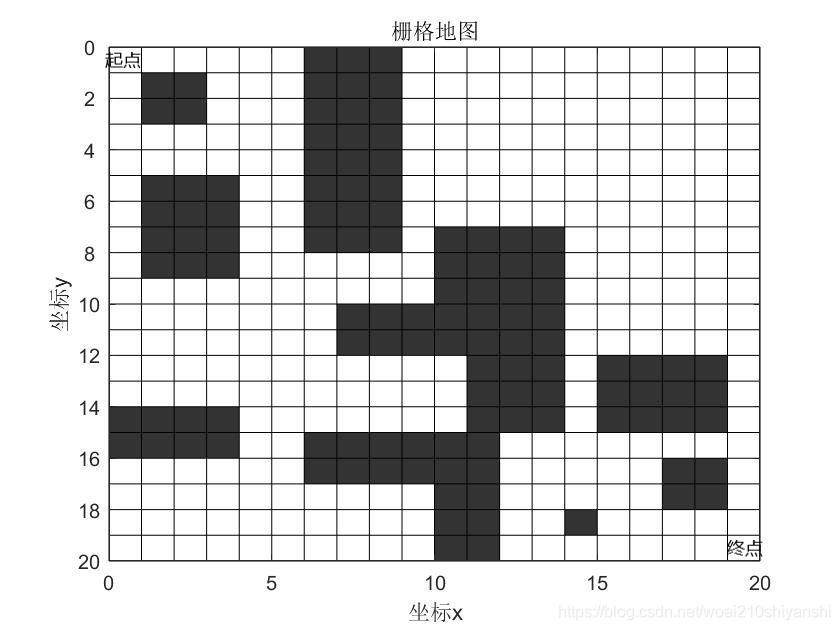
图1　栅格法地图
在用栅格法建立环境模型时，为了将环境信息转换成移动机器人可以识别的数据，一般采用序号法标记环境地图信息，即将栅格地图中一个个栅格从序号１依次累加直到标记到最后一个栅格。如图2所示。


图3　八叉树搜索策略
那么，怎么判断一个栅格点是否为另一个栅格点的相邻栅格点呢，另外，又怎么判断是否为有障碍栅格呢。这就需建立矩阵D，记录每个栅格点至其相邻栅格点的代价值。本例中栅格地图有20×20个栅格点，则D的大小为400×400，其中列是起点栅格，行是局部终点栅格，各栅格点至其各相邻无障碍栅格点的代价值非零，而有障碍栅格及非相邻栅格设为0。

二、部分源代码

clc
clear
close all
tic
%% 地图
G=[0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0; 
   0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
   0 1 1 1 0 0 1 1 1 0 1 1 1 1 0 0 0 0 0 0; 
   0 1 1 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 1 1 0 1 1 1 1 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 1 1 0 1 1 1 1 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 1 0; 
   0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 1 0; 
   1 1 1 1 0 0 0 0 0 0 0 0 1 1 0 1 1 1 1 0; 
   1 1 1 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 1 1 0 1 1 1 0 0 0 0 0 1 1 0; 
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0; 
   0 0 1 1 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0;];
for i=1:20/2
    for j=1:20
        m=G(i,j);
        n=G(21-i,j);
        G(i,j)=n;
        G(21-i,j)=m;
    end
end
%% 
S = [1 1];   
E = [20 20];  
G0 = G;
G = G0(S(1):E(1),S(2):E(2)); 
[Xmax,dimensions] = size(G);        
dimensions = dimensions - 2;             

%% 参数设置
max_gen = 200;    % 最大迭代次数
num_polution = 50;         % 种群数量
soft_value = 0.8;        %安全值
recover_Percent = 0.3;  %%发现者比例
scout_Percent = 0.2;  %%侦查者比例
recover_Num = round( num_polution * recover_Percent );    % %发现者
scout_Num = round(num_polution * scout_Percent);      %%侦查者数量
X_min = 1;  

%% 初始化
X = zeros(num_polution,dimensions);
for i = 1:num_polution
    for j = 1:dimensions
       column = G(:,j+1);      % 地图的一列
       id = find(column == 0); % 该列自由栅格的位置
       X(i,j) =  id(randi(length(id))); % 随机选择一个自由栅格
       id = [];
    end 
    fit( i ) = fitness(X( i, : ),G);%%%行向量
end
fit_person_best = fit;   % 个体最优适应度
person_best = X;      % 个体最优位置
[fit_global_best, best_person_Index] = min( fit );        % 全局最优适应度
global_best = X(best_person_Index, : );    % 全局最优位置
[fit_max,B]=max(fit);
worse_person= X(B,:);  
%%
for gene = 1:max_gen
    gene
    [ans1,sort_Index] = sort(fit);   %适应值度从小到大排序
    [fit_max,B] = max(fit);
    worse_person = X(B,:);           %找出适应度最差的个体
    [~,Index] = sort(fit_person_best);
    r2 = rand(1);
    if r2 < soft_value

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

        for i = 1:recover_Num                                                  
            r1 = rand(1);  
            X(Index(i),:) = person_best(Index(i),:)*exp(-(i)/(r1*max_gen));         %%%%%发现者广泛进行搜索操作
            X(Index(i),:) = Bounds(X(Index(i),:), X_min,Xmax);                      %%%%输出整数路径
            fit(Index(i)) = fitness(X(Index(i),:),G);
        end
    else
            X(Index(i),:) = person_best(Index(i),:) + randn(1)*ones(1,dimensions);  %%%%%%%飞往其他地方觅食
            X(Index(i),:) = Bounds(X(Index(i),:),X_min,Xmax);    
            fit(Index(i)) = fitness(X(Index(i),:),G);
    end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%发现者%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    [fit_MMin,best_best] = min(fit);      
    best_best_bt = X(best_best,:);     
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    for i = (recover_Num+1):num_polution                   
        A = floor(rand(1,dimensions)*2)*2-1;                %%%%%%%%-1到1的随机数
        if(i>(num_polution/2))
            X(Index(i),:) = randn(1)*exp((worse_person-person_best(Index(i),:))/(i)^2);%%%%%%%适应度较低的个体没有获得食物，将飞往其他地方随机范围
        else
            X(Index(i),:) = best_best_bt+(abs((person_best(Index(i),:)-best_best_bt)))*(A'*(A*A')^(-1))*ones(1,dimensions); %%%%%%%中等适应度值的个体更新位置
        end
        X(Index(i),:) = Bounds(X(Index(i),:),X_min,Xmax);
        fit(Index(i)) = fitness(X(Index(i),:),G);
    end
    p_1 = randperm(numel(sort_Index));
    p_2 = sort_Index(p_1(1:scout_Num));
    for j = 1:length(p_2)     
        if(fit_person_best(Index(p_2(j)))>(fit_global_best))
            X(Index(p_2(j)),:) = global_best+(randn(1,dimensions)).*(abs((person_best(Index( p_2(j)),:) -global_best)));%%%%%%%%意识到危险的麻雀向种群适应度最高的个体靠拢
        else
            如何用MATLAB求解0-1整数规划?

 求用动态规划的方法求解简单的整数规划问题的matlab程序或者C++程序代码，高手们帮帮忙
 matlab整数规划程序
 如何用matlab求解0-1规划问题
 用matlab编程解决整数规划
 如何用matlab求解0-1规划问题?