(计算机组成原理)第二章数据的表示和运算-第三节1：浮点数的表示

Posted 2021-09-03 快乐江湖

文章目录

• 一：浮点数的表示格式
• 二：浮点数尾数的规格化
• • （1）左规和右规
  • （2）规格化浮点数的特点
• 三：浮点数表示范围（408考试大纲已删除）

浮点表示法是指以适当的方式将比例因子表示在数据中，让小数点的位置根据需要而浮动
这样，在位数有限的情况下，即扩大了数的表示范围，又保持了数的有效进度。例如，用定点数表示电子的质量（$9\times 10^{-28}g$）或太阳的质量（$2\times 3^{33}g$）是非常不方便的

一：浮点数的表示格式

在小学学习科学计数时，我们知道对于：$[phone]\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}$这么长的数字可以用科学计数法表示为：
$$+3.026\times 10^{11}$$

而浮点数的表示格式与科学计数法有异曲同工之妙

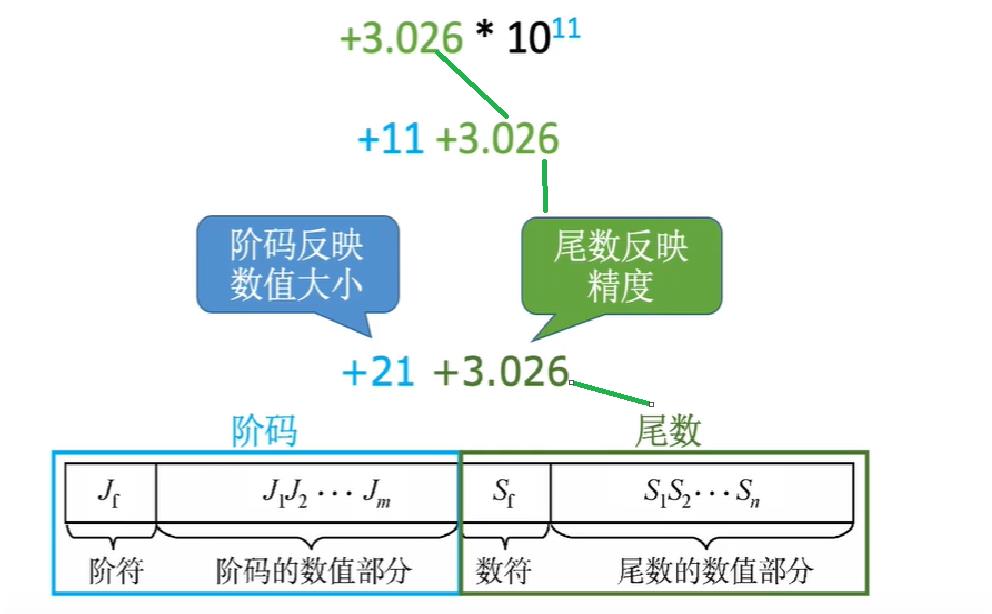
• 阶码：反映浮点数的表示范围及小数点的实际位置
• 尾数：其数值部分的位数$n$反映了浮点数的精度
  因此，通常浮点数表示为：
  $$N=r^E\times M$$

其中$r$是浮点数阶码的底（隐含），与尾数的基数相同（二进制中$r=2$），E是阶码，是一个常用补码或移码表示的定点整数，M是尾数，是一个常用原码或补码表示的定点小数

因此，这种格式可以这样理解：尾数给出了一个小数（数符指明其正负性），同时阶码指明了小数点要向前（阶符为负）还是向后（阶符为正）移动几位

---

$case1:$例如浮点数a的阶码（补码）为$0,01$，尾数（补码）为$1.1001$，空间中存储的方式就是下面这样的

a的阶码对应的真值为+1，尾数对应的真值为=-($2^{-2}+2^{-3}+2^{-4}$)=-$0.0111$，则a的真值为：$2^1\times (-0.0111)=-0.111$

$case2$：例如b的阶码（补码）为$0,10$，尾数（补码）为$0.01001$，空间存储如下

• 上述后面1被抛弃了，精度丢失

b的阶码对应真值为+2，尾数对应真值为$+(2^{-2}+2^5)=+0.01001$，因此b的真值为：$2^2\times (+0.01001)=+1.001$

二：浮点数尾数的规格化

（1）左规和右规

可以看到，上面的$case2$中，由于尾数位数不够，因此最后一位1丢失，导致该种表示方法下的浮点数精度丢失。就像我们在学习科学计数法的时候要求过的一样，尽量保证不要超炫$0.003\times 10^{13}$这样的形式出现，必须保证最高位是一个有效位，因为无效的0不但不会增加精度，反而会占用位数。

因此为了提高运算的精度，需要充分利用尾数的有效数位，通常采取浮点数规格化形式，即规定尾数的最高数位必须是一个有效值。非规格化浮点数需要进行规格化操作才能变成规格化浮点数。所谓规格化操作，是指通过调整一个非规划浮点数的尾数和阶码的大小，使非零的浮点数在尾数的最高位上保证是一个有效值。

规格化方法主要有两种

• 左规：将尾数算数左移一位，阶码就减1（基数为2），左规可能要进行多次

• 右规：当浮点数运算的结果尾数出现溢出（双符号位为01或10）时，将尾数算数右移一位，阶码加1（基数为2时） 的方法称为右规，右规只需进行一次。

下面是一个需要右规的例子

（2）规格化浮点数的特点

规格化浮点数的尾数$M$的绝对值应该满足$\frac{1}{r}\le |M|\le 1$，若$r$为2，则有$\frac{1}{2}\le |M|\le 1$。规格化表示的尾数形式如下

1：原码规格化后

规格化的原码尾数，最高数值位一定是1

• 正数：形式为0.1××...×，其最大值表示为0.111...1，最小值表示为0.100...0，尾数的表示范围为$\frac{1}{2}\le M\le (1-2^{-n})$
• 负数：形式为1.1××...×，其最大值表示为1.10×××0，最小值表示为1.111...1，尾数的表示范围为$-\frac{1}{2}\ge M\ge -(1-2^{-n})$

2：补码规格化后

规格化的补码尾数，符号位与最高数值位一定相反

• 正数：形式为0.1××...×，其最大值表示为0.111...1，最小值表示为0.100...0，尾数的表示范围为$\frac{1}{2}\le M\le (1-2^{-n})$
• 负数：形式为1.0××...×，其最大值表示为1.01×××1，最小值表示为1.00...0，尾数的表示范围为$-1\le M\le -(\frac{1}{2}+2^{-n})$

---

$case3：$若某浮点数的阶码，尾数用补码表示，共4+8位：0.110;1.1110100，问如何规格化？

答：在这个例子中，阶数为+6，前面说过我们规定规格化的补码尾数的负数形式一定为1.0××...×，因此可以将1.1110100算数左移三位（补码的算数左移是低位补0，算数右移是高位补1），结果为1.010000，阶码变为+3。

三：浮点数表示范围（408考试大纲已删除）

如下图所示，运算结果大于最大正数时称为正上溢，小于绝对值最大负数时称为负上溢，正上溢和负上溢统称为上溢。数据一旦产生上溢，计算机必须进行中断操作，进行溢出处理。

当运算结果在0到最小正数之间时称为正下溢，在0到绝对值最小负数之间时称为负下溢，正下溢和负下溢统称为下溢，数据下溢时，浮点数区域0，计算机仅将其当做机器零处理