(计算机组成原理)第二章数据的表示和运算-第二节4：定点数的加减运算和溢出判断
Posted 快乐江湖
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了(计算机组成原理)第二章数据的表示和运算-第二节4：定点数的加减运算和溢出判断相关的知识，希望对你有一定的参考价值。
文章目录
一：使用原码实现加减法基本逻辑
（1）原码加法
正数+正数： 使用绝对值做加法，结果为正
负数+负数： 使用绝对值做加法，结果为负
正数+负数或负数+正数： 绝对值大的减去绝对值小的，符号同绝对值大的数
- 注意正数+正数、负数+负数这两种情况结果可能会溢出
（2）原码减法
根据之前的描述我们可以知道，减法可以用等价的加法来实现，所以减数符号取反转变为加法
正数-负数： 正数+正数
负数-正数： 负数+负数
正数-正数： 正数+负数
负数+正数： 负数-负数
二：使用补码实现加减法
可以看出使用原码完成加减运算实在是有点难为计算机了，而且实现逻辑极其复杂。所以在计算机中是使用补码完成加减法运算的。
设机器字长为8位， A = 15 A=15 A=15， B = − 24 B=-24 B=−24，求 [ A + B ] 补 [A+B]_{补} [A+B]补和 [ A − B ] 补 [A-B]_{补} [A−B]补
运算时莫管符号位，直接相加就可以了：
[
A
+
B
]
补
=
[
A
]
补
+
[
B
]
补
=
0
,
0001111
+
1
,
1110111
=
1
,
1110111
[A+B]_{补}=[A]_{补}+[B]_{补}=0,0001111+1,1110111=1,1110111
[A+B]补=[A]补+[B]补=0,0001111+1,1110111=1,1110111，转为原码为
1
,
0001001
1,0001001
1,0001001，真值为
−
9
-9
−9
[ A − B ] 补 [A-B]_{补} [A−B]补= [ A ] 补 + [ − B ] 补 = 0 , 0001111 + 0 , 0011000 = 0 , 0100111 [A]_{补}+[-B]_{补}=0,0001111+0,0011000=0,0100111 [A]补+[−B]补=0,0001111+0,0011000=0,0100111，转换为原码为 0 , 0100111 0,0100111 0,0100111，真值为+39
- 小技巧： [ − B ] 补 = [ B ] 补 全 部 位 （ 包 括 符 号 位 ） 取 反 后 + 1 [-B]_{补}=[B]_{补}全部位（包括符号位）取反后+1 [−B]补=[B]补全部位（包括符号位）取反后+1
因此对于补码来说，无论加法还是减法，最后都会转换为加法，由加法器实现运算，符号一同参与运算
三：溢出判断
在上面的例子中加入
C
=
124
C=124
C=124，请你求
[
A
+
C
]
补
[A+C]_{补}
[A+C]补和
[
B
−
C
]
补
[B-C]_{补}
[B−C]补
相信运算过后你会得到一个奇怪的结果
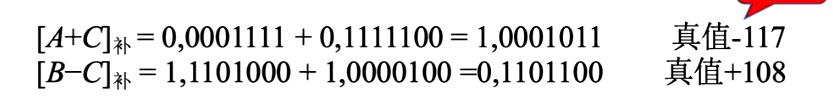
这是因为如果机器字长8位，那么它表示的范围就是 − 128 − 127 -128-127 −128−127，所以上面的例子发生了溢出的现象
溢出分为上溢和下溢
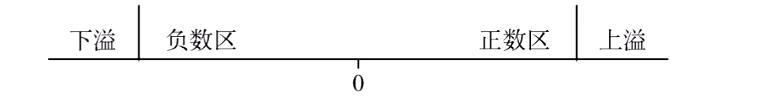
- 正数+正数导致上溢：正+正=负
- 负数+负数导致下溢：负+负=正
（1）采用一位符号位依据溢出表达式判断
依照上面溢出的例子有
[
A
+
C
]
补
=
0
,
0001111
+
0
,
1111100
=
1
,
0001011
[A+C]_{补}=0,0001111+0,1111100=1,0001011
[A+C]补=0,0001111+0,1111100=1,0001011，真值-117
[
B
−
C
]
补
=
1
,
1101000
+
1
,
0000100
=
0
,
1101100
[B-C]_{补}=1,1101000+1,0000100=0,1101100
[B−C]补=1,1101000+1,0000100=0,1101100，真值+108
假设A的符号位为
A
s
A_{s}
As，B的符号位为
B
S
B_{S}
BS，其运算结果符号位
S
s
S_{s}
Ss，则溢出逻辑表达式为
V
=
(
A
s
B
s
(
¬
S
s
)
)
+
(
(
¬
A
s
)
(
¬
B
s
)
S
s
)
V=(A_{s}B_{s}(\\neg S_{s} ))+ ((\\neg A_{s})( \\neg B_{s})S_{s})
V=(AsBs(¬Ss))+((¬As)(¬Bs)Ss)
若 V = 0 V=0 V=0表示无溢出； V = 1 V=1 V=1表示有溢出
- 与： A B C ABC ABC表示与运算，A与B与C，当A、B、C全部为1时结果为1，有一个为0结果为0
- 或： A + B + C A+B+C A+B+C表示或运算，A或B或C，当A、B、C全部为0时结果为0，有一个为1结果为1
- 非： ¬ A \\neg A ¬A表示非运算，比如 A A A为1则 ¬ A \\neg A ¬A为0
因此在上面的例子中 [ A ] 补 [A]_{补} [A]补符号位为0， [ C ] 补 [C]_{补} [C]补符号位为0，， ¬ [ A + C ] 补 \\neg [A+C]_{补} ¬[A+C]补结果为0，逻辑运算结果为0；又 ¬ [ A ] 补 \\neg [A]_{补} ¬[A]补为1， ¬ [ C ] 补 \\neg [C]_{补} ¬[C]补为1，， [ A + C ] 补 [A+C]_{补} [A+C]补符号位为1
也就是$V= 000 + 111 = 0 + 1 = 1 000 + 111=0+1=1 000+111=0+1=1于是有溢出，其实这也对应了正数+正数必由溢出的结论$ 。 同时负数+负数，也就是 [ B − C ] 补 [B-C]_{补} [B−C]补读者可以根据上面的逻辑自行验证，会发现也是溢出的。
于是通过这种方法我们就把电路的思想通过数学表达式表现了除了，计算机在判断溢出时可根据此逻辑进行判断
（2）采用一位符号位依据进位情况判断
这里有两个进位需要区别开来
- 符号位的进位 C s C_{s} Cs：最高数值位向符号位进的位
- 最高数值位的进位
C
1
C_{1}
C1：最高数值位得到的进位
如果
以上是关于(计算机组成原理)第二章数据的表示和运算-第二节4：定点数的加减运算和溢出判断的主要内容，如果未能解决你的问题，请参考以下文章 (计算机组成原理)第二章数据的表示和运算-第二节5：定点数乘法运算（原码/补码一位乘法） (计算机组成原理)第二章数据的表示和运算-第二节6：定点数除法运算（原码/补码一位除法） (计算机组成原理)第二章数据的表示和运算-第二节3：定点数的移位运算（算数移位逻辑移位和循环移位） (计算机组成原理)第二章数据的表示和运算-第二节1：定点数的表示（原码反码补码和移码）