(计算机组成原理)第二章数据的表示和运算-第二节1：定点数的表示（原码反码补码和移码）
Posted 快乐江湖
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了(计算机组成原理)第二章数据的表示和运算-第二节1：定点数的表示（原码反码补码和移码）相关的知识，希望对你有一定的参考价值。
一：机器数的定点表示
根据小数点的位置是否固定，在计算机中有两种数据格式表示方法：定点表示和浮点表示。浮点表示类似于科学计数法，将在第三节介绍
定点表示就是约定机器数中的小数点位置固定不变，小数点不再使用.表示，而是约定其位置。理论上，小数点位置固定在任何一位都可以，但是在计算机中通常采用两种简单的约定：将小数点的位置固定在数据的最高位之前，称其为定点小数；或固定在最低位之后，称其为定点整数
(定点整数)
(定点小数)
二：无符号数和有符号数的表示
（1）无符号数
无符号数是指整个机器字长的全部二进制位均为数值位，没有符号位，相当于数的绝对值; n n n位无符号数的能表示的数的**范围为 ( 0 , 2 n − 1 ) ∗ ∗ (0,2^{n}-1)** (0,2n−1)∗∗;通常 只有无符号整数，而没有无符号小数
（2）有符号数
在机器中，数的正和负是无法识别的，有符号数用"0"表示正，用"1"表示负，从而将符号数值化，通常约定二进制数位的最高位为符号位。
有符号数可以表示定点整数和定点小数，所以可以用原码、反码、补码三种方式表示定点整数和定点小数，还可以用移码表示定点整数。如果真值为 x x x，则用 [ x ] 原 [x]_{原} [x]原、 [ x ] 反 [x]_{反} [x]反、 [ x ] 补 [x]_{补} [x]补、 [ x ] 移 [x]_{移} [x]移分别表示真值对应的原码、反码、补码和移码。
三：原码、补码、反码和移码
（1）原码
原码是一种比较简单、直观的机器数表示法。用机器数的最高位表示该数的符号，其余的各位表示数的绝对值。其中0表示正，1表示负
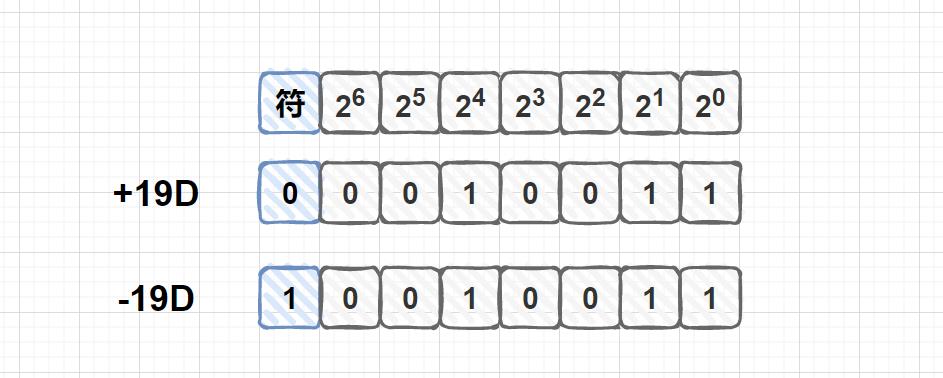
比如 19.75 19.75 19.75这个数字，假设机器字长为8位
A：定点整数的原码表示
按照二进制的位权书写即可，不足位可以用0补齐，常写作
[
x
]
原
=
1
,
0010011
[x]_{原}=1,0010011
[x]原=1,0010011
这里若机器字长为
n
+
1
n+1
n+1位，那么原码整数的表示范围为
−
(
2
n
−
1
)
⩽
x
⩽
2
n
−
1
-(2^{n}-1) \\leqslant x \\leqslant 2^{n}-1
−(2n−1)⩽x⩽2n−1
需要注意的是真值0有 + 0 +0 +0和 − 0 -0 −0两种形式
B：定点小数的原码表示
按照二进制的位权书写即可，不足位可以用0补齐，常写作
[
x
]
原
=
1.1100000
[x]_{原}=1.1100000
[x]原=1.1100000
这里若机器字长为
n
+
1
n+1
n+1位，那么原码小数的表示范围为
−
(
1
−
2
−
n
)
⩽
x
⩽
1
−
2
−
n
-(1-2^{-n}) \\leqslant x \\leqslant 1-2^{-n}
−(1−2−n)⩽x⩽1−2−n
需要注意的是真值0有 + 0 +0 +0和 − 0 -0 −0两种形式
（2）反码
反码是原码转换为补码的一个中间状态。
1：如果为正数，则反码与原码相同
例如+19D，其
[
x
]
原
=
0
,
0010011
[x]_{原}=0,0010011
[x]原=0,0010011，
[
x
]
反
=
0
,
0010011
[x]_{反}=0,0010011
[x]反=0,0010011
例如+0.75D，其
[
x
]
原
=
0.1100000
[x]_{原}=0.1100000
[x]原=0.1100000，
[
x
]
反
=
0.1100000
[x]_{反}=0.1100000
[x]反=0.1100000
2：如果为负数，则除符号位外，其他位按位取反
例如-19D，其
[
x
]
原
=
1
,
0010011
[x]_{原}=1,0010011
[x]原=1,0010011，
[
x
]
反
=
1
,
1101100
[x]_{反}=1,1101100
[x]反=1,1101100
例如-0.75D，其
[
x
]
原
=
1.1100000
[x]_{原}=1.1100000
[x]原=1.1100000，
[
x
]
反
=
1.0011111
[x]_{反}=1.0011111
[x]反=1.0011111
需要特别注意真值0的+0和-0这两种形式
[
+
0
]
原
=
00000000
[+0]_{原}=00000000
[+0]原=00000000，
[
−
0
]
原
=
10000000
[-0]_{原}=10000000
[−0]原=10000000
[
+
0
]
反
=
00000000
[+0]_{反}=00000000
[+0]反=00000000，
[
−
0
]
反
=
11111111
[-0]_{反}=11111111
[−0]反=11111111
（3）补码
1：如果为正数，则补码和原码一致
例如+19D，其
[
x
]
原
=
0
,
0010011
[x]_{原}=0,0010011
[x]原=0,0010011，
[
x
]
反
=
0
,
0010011
[x]_{反}=0,0010011
[x]反=0,0010011，
[
x
]
补
=
0
,
0010011
[x]_{补}=0,0010011
[x]补=0,0010011
例如+0.75D，其
[
x
]
原
=
0.1100000
[x]_{原}=0.1100000
[x]原=0.1100000，
[
x
]
反
=
0.1100000
[x]_{反}=0.1100000
[x]反=0.1100000，
[
x
]
补
=
0.1100000
[x]_{补}=0.1100000
[x]补=0.1100000
2：如果为负数，则补码=反码+1，需要注意进位
例如-19D，其
[
x
]
原
=
1
,
0010011
[x]_{原}=1,0010011
[x]原=1,0010011，
[
x
]
反
=
1
,
1101100
[x]_{反}=1,1101100
[x]反=1,1101100，
[
x
]
补
=
1
,
1101101
[x]_{补}=1,1101101
[x]补=1,1101101
例如-0.75D，其
[
x
]
原
=
1.1100000
[x]_{原}=1.1100000
[x]原=1.1100000，
[
x
]
反
=
1.0011111
[x]_{反}=1.0011111
[x]反=1.以上是关于(计算机组成原理)第二章数据的表示和运算-第二节1：定点数的表示（原码反码补码和移码）的主要内容，如果未能解决你的问题，请参考以下文章
(计算机组成原理)第二章数据的表示和运算-第二节5：定点数乘法运算（原码/补码一位乘法）
(计算机组成原理)第二章数据的表示和运算-第二节6：定点数除法运算（原码/补码一位除法）
(计算机组成原理)第二章数据的表示和运算-第二节3：定点数的移位运算（算数移位逻辑移位和循环移位）
(计算机组成原理)第二章数据的表示和运算-第二节7：详解C语言中的强制类型转换