国科大人工智能学院《计算机视觉》课 —三维视觉—相机模型与多视几何

Posted 2021-08-29 鱼米粒

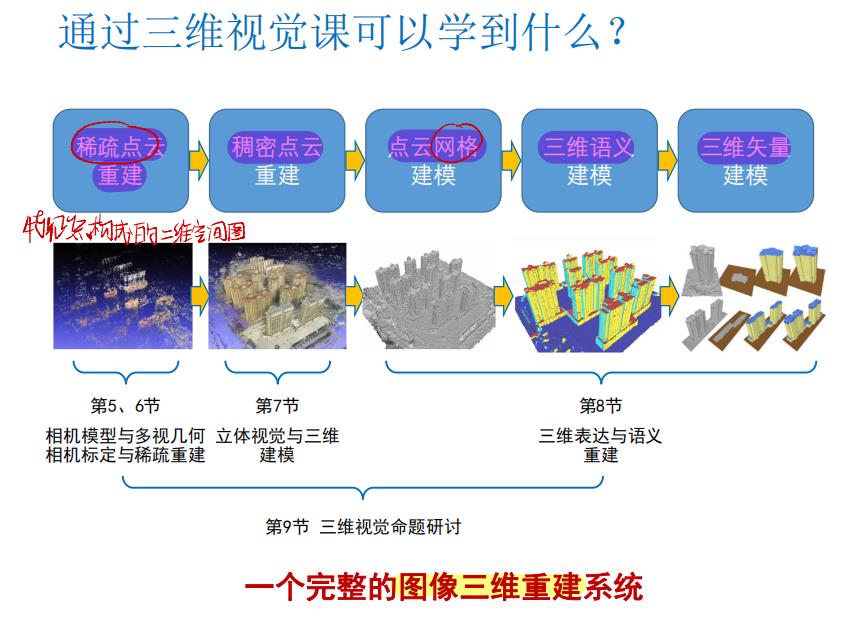
零、三维计算机视觉 涉及的知识

1. 相机模型与多视几何
2. 相机标定与稀疏重建
3. 立体视觉与三维建模
4. 三维表达与语义重建
   
   
   

---

一、相机成像：三维 —> 二维

1. 小孔成像

屏障上的“小孔”称为“光圈Aperture”

• 小光圈：曝光时间增长，高亮度图像
• 大光圈：曝光时间短，模糊图像
• 光圈变小：图像先变清晰，再变模糊
• 因为光圈过小，会产生衍射现象，导致图像模糊

2. 透镜系统

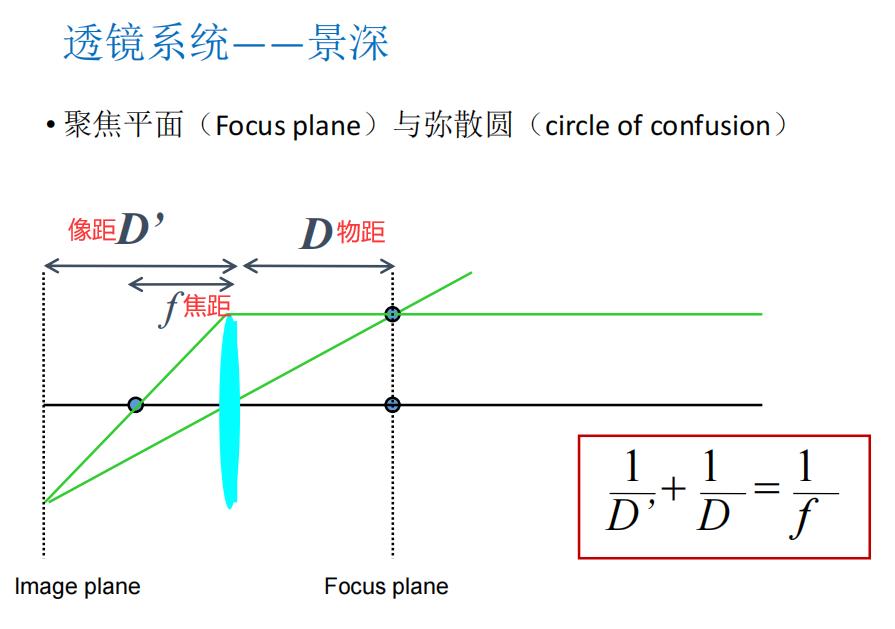
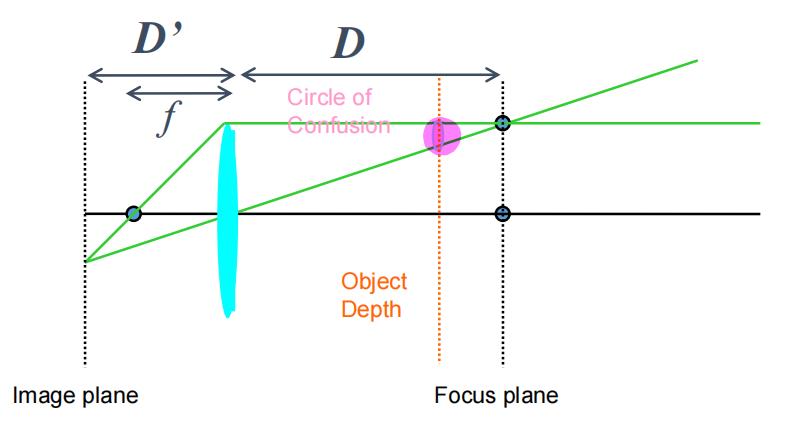
• 景深：清晰成像的范围
• 弥散圆：在平面上成的像会成为有一定直径的圆

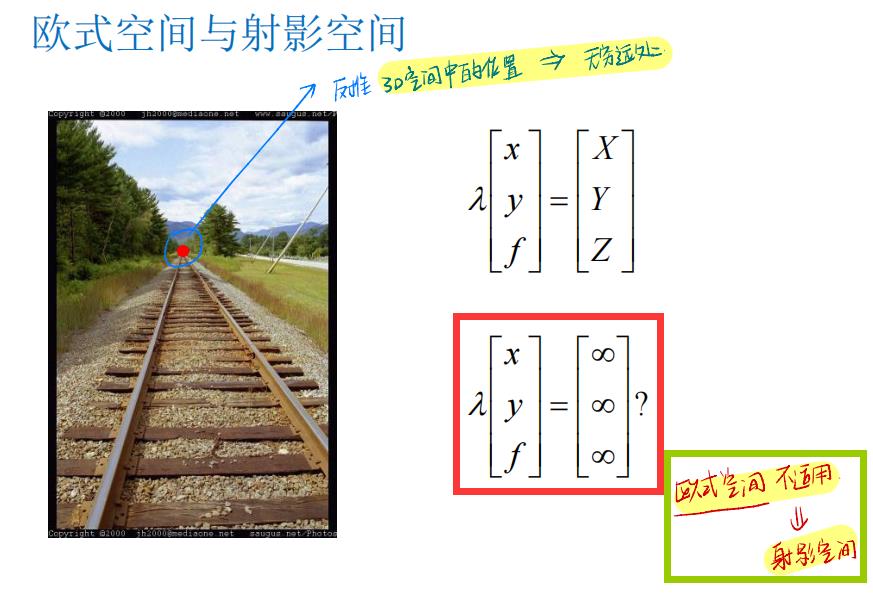
3. 欧式空间和射影空间

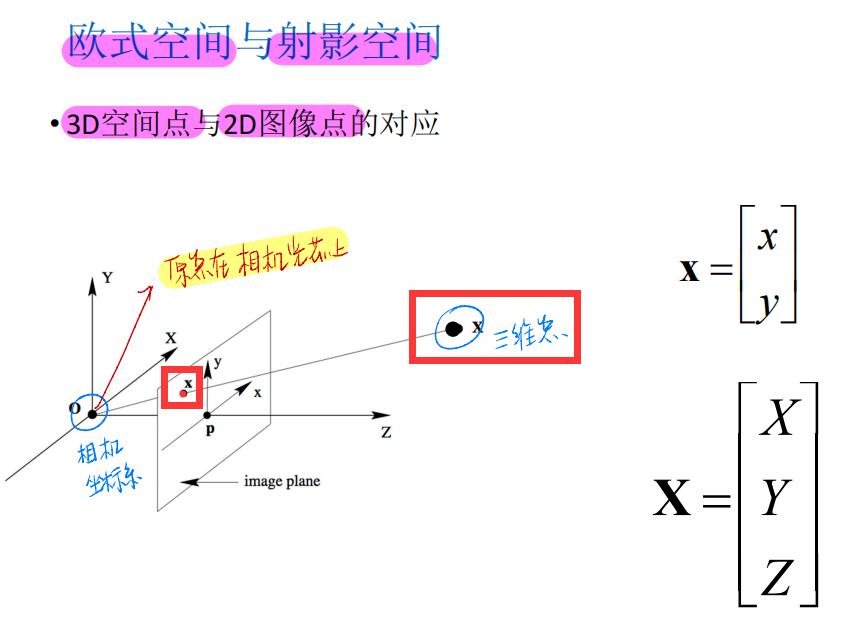
三维空间点 与 二维图像点 对应：

但欧式空间中对于三维空间中无穷远处的点无法表达：

所以射影空间为：把无穷远处的元素包含进来

• 欧式空间：存在无穷远的概念，但是不参与计算
• 射影空间：对n维欧式空间加入无穷远元素，并对有限元素和无穷远元素不加以区分。

4. 齐次坐标：齐次坐标是 射影空间 的坐标表达方式

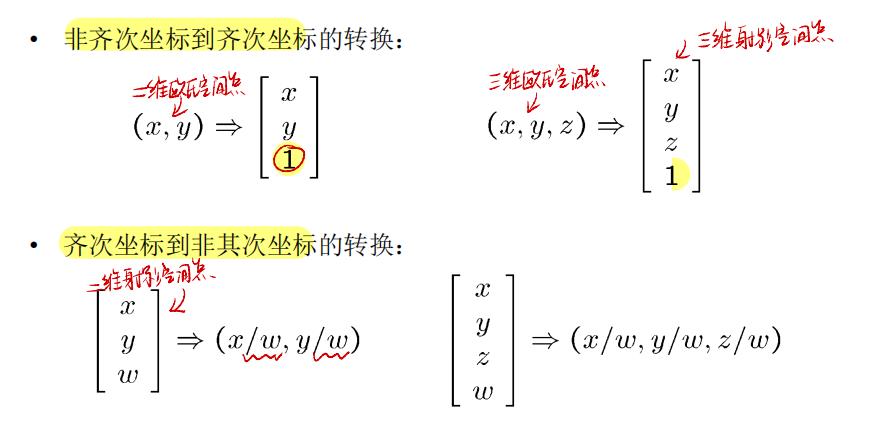
二、相机模型

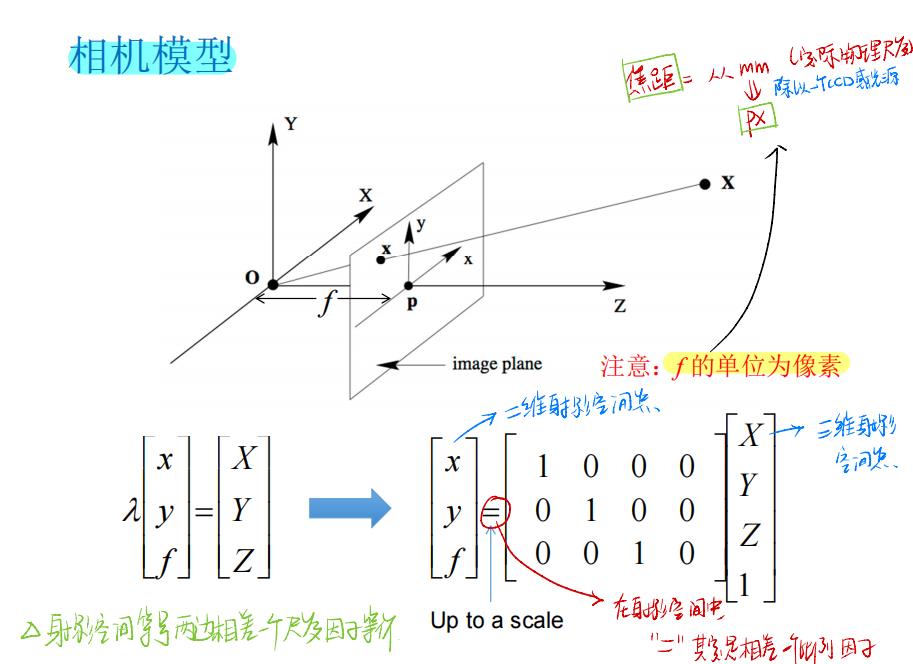
1. 坐标系：相机坐标系、世界坐标系

2. 坐标变换

相机位姿R和t 是相对于 世界坐标系 而言的。

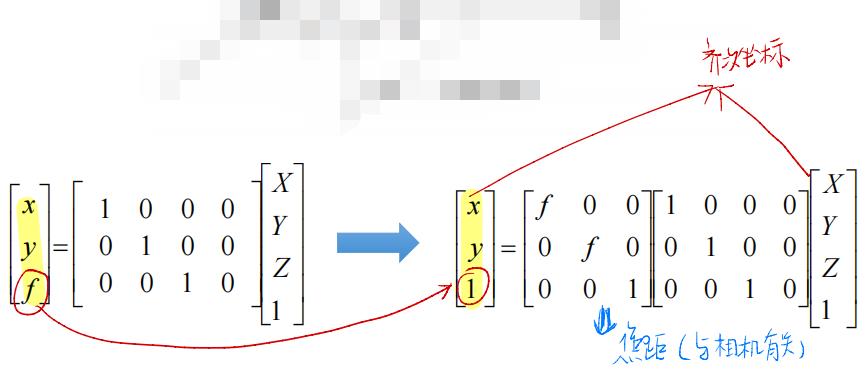
3. 相机模型

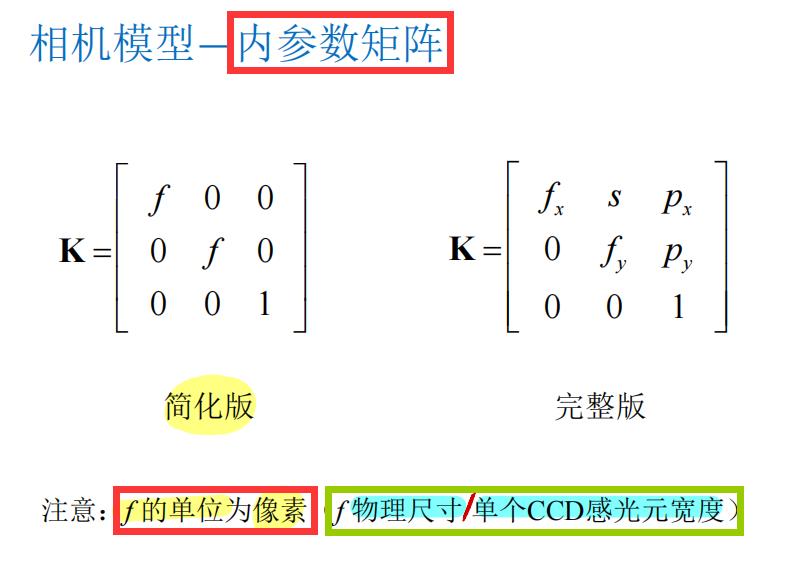
4. 镜头畸变

三、多视（多个不同视角的图像）几何

1. 两视图几何

极平面epipolar plane 将 三维点、二维点、相机 结合。（将已知量与未知量约束。）

2. 基本矩阵F

用数学方式来刻画 极平面：基本矩阵F

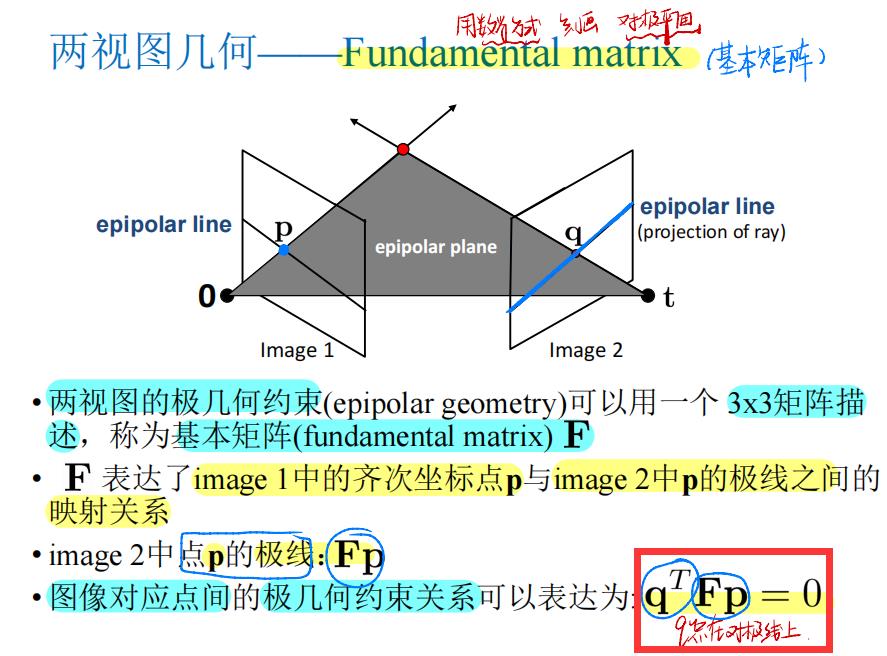
基本矩阵F秩为2，不满秩。

3. 8点法求F

通过8组图像对应点，求基本矩阵F。

4. 本质矩阵E：假设相机内参数已知（5点法就可求出E）

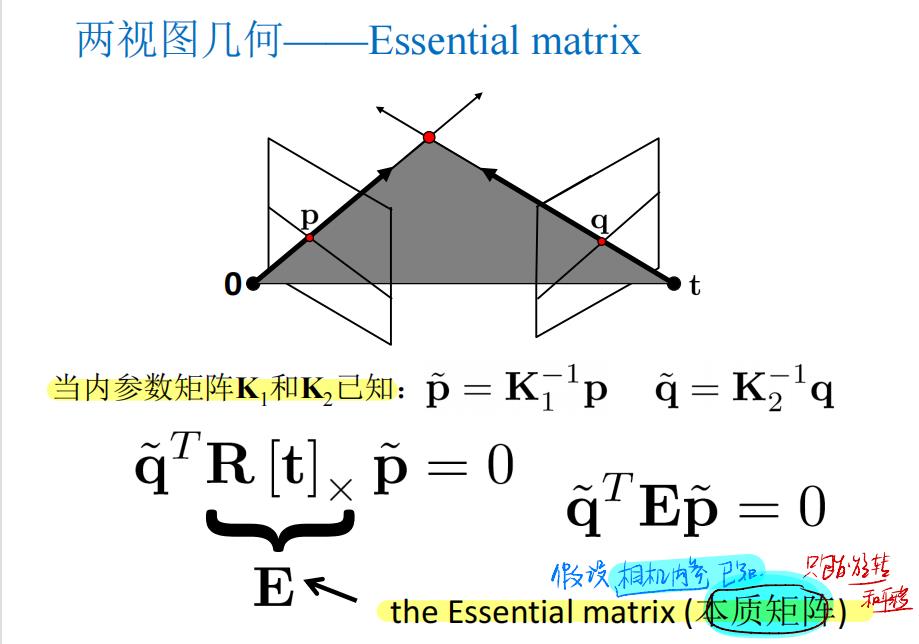
5. 最小配置解