时间复杂度&空间复杂度分析

Posted 2022-04-18 午饭要阳光

时间复杂度：   一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数f(n)，进而分析f(n)随n的变化情况并确定T(n)的数量级。这里用"O"来表示数量级，给出算法的时间复杂度。                      T(n)=O(f(n));   它表示随着问题规模的n的增大，算法的执行时间的增长率和f(n)的增长率相同，这称作算法的渐进时间复杂度，简称时间复杂度。而我们一般讨论的是最坏时间复杂度，这样做的原因是：最坏情况下的时间复杂度是算法在任何输入实例上运行时间的上界，分析最坏的情况以估算算法指向时间的一个上界。
时间复杂度的分析方法： 1、时间复杂度就是函数中基本操作所执行的次数 2、一般默认的是最坏时间复杂度，即分析最坏情况下所能执行的次数 3、忽略掉常数项 4、关注运行时间的增长趋势，关注函数式中增长最快的表达式，忽略系数 5、计算时间复杂度是估算随着n的增长函数执行次数的增长趋势 6、递归算法的时间复杂度为：递归总次数 * 每次递归中基本操作所执行的次数
    常用的时间复杂度有以下七种，算法时间复杂度依次增加：O(1)常数型、O(log2 n)对数型、O(n)线性型、O(n log2 n)二维型、O(n^2)平方型、O(n^3)立方型、O(2^n)指数型.


空间复杂度：   算法的空间复杂度并不是计算实际占用的空间，而是计算整个算法的辅助空间单元的个数，与问题的规模没有关系。算法的空间复杂度S(n)定义为该算法所耗费空间的数量级。   S(n)=O(f(n))   若算法执行时所需要的辅助空间相对于输入数据量n而言是一个常数，则称这个算法的辅助空间为O(1);    递归算法的空间复杂度：递归深度N*每次递归所要的辅助空间， 如果每次递归所需的辅助空间是常数，则递归的空间复杂度是 O(N).

例： 1、求二分法的时间复杂度和空间复杂度。 非递归：

template<typename T>
T* BinarySearch(T* array,int number,const T& data)

       assert(number>=0);
       int left = 0;
       int right = number-1;
       while (right >= left)
       
              int mid = (left&right) + ((left^right)>>1);
              if (array[mid] > data)
              
                     right = mid - 1;
              
              else if (array[mid] < data)
              
                     left = mid + 1;
              
              else
              
                     return (array + mid);
              
       
       return NULL;

分析：

循环的基本次数是 log2 N ，所以: 时间复杂度是O( log2  N); 由于辅助空间是常数级别的所以： 空间复杂度是O(1);

递归：

template<typename T>
T* BinarySearch(T* left,T* right,const T& data)

       assert(left);
       assert(right);
       if (right >=left)
       
              T* mid =left+(right-left)/2;
              if (*mid == data)
                     return mid;
              else
                     return *mid > data ? BinarySearch(left, mid - 1, data) : BinarySearch(mid + 1, right, data);
       
       else
       
              return NULL;
       

递归的次数和深度都是 log2  N,每次所需要的辅助空间都是常数级别的： 时间复杂度:O( log2 N ) 空间复杂度：O( log2 N )


2、斐波那契数列的时间和空间复杂度 //递归情况下的斐波那契数列

long long Fib(int n)

       assert(n >= 0);
       return n<2 ? n : Fib(n - 1) + Fib(n-2);

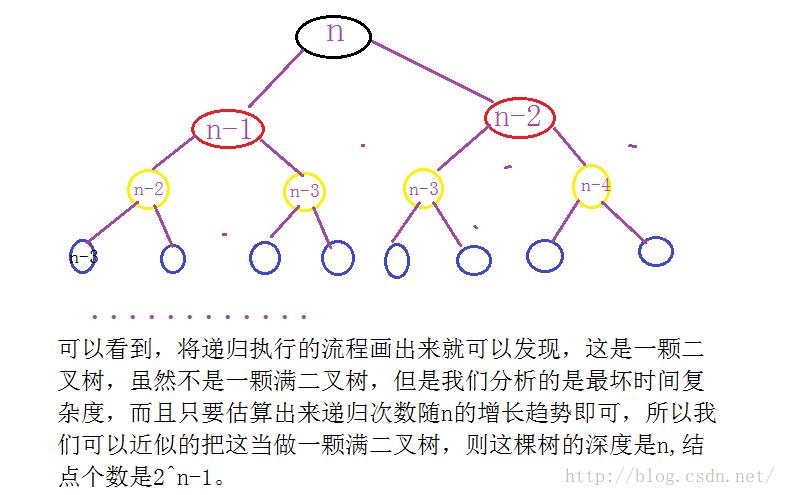
递归的时间复杂度是：  递归次数*每次递归中执行基本操作的次数 所以时间复杂度是： O(2^N) 递归的空间复杂度是：  递归的深度*每次递归所需的辅助空间的个数 所以空间复杂度是：O(N)


//求前n项中每一项的斐波那契数列的值

long long *Fib(int  n)

       assert(n>=0);
       long long *array = new long long[n + 1];
       array[0] = 0;
       if (n > 0)
       
              array[1] = 1;
       
       for (int i = 2; i <n+1; i++)
       
              array[i] = array[i - 1] + array[i - 2];
       
       return array;

循环的基本操作次数是n-1,辅助空间是n+1，所以： 时间复杂度O(n) 空间复杂度O(n)

//非递归

long long Fib(int n)

       assert(n >= 0);
       long long first=0,second=1;
       for (int i = 2; i <= n; i++)
       
              first = first^second;
              second = first^second;
              first = first^second;
              second = first + second;
       
       return second;

循环的基本次数是n-1，所用的辅助空间是常数级别的： 时间复杂度：O(n) 空间复杂度：O(1)