数据结构--复杂度

Posted 2021-05-16 水澹澹兮生烟.

在评价一个算法的优劣势，需要计算其算法效率。算法效率分析分为两种：第一种是时间效率，第二种是空间效率。时间效率被称为时间复杂度，而空间效率被称作空间复杂度。

1.时间复杂度

算法中的基本操作的执行次数，为算法的时间复杂度。一般用O的渐进法表示。
推导O阶方法：
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中，只保留最高阶项。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。
**例子：
斐波那契数列：

unsigned long long Fib(int n){//效率太差了，O(2^n)
	if(n<3)  return 1;
	return Fib(n-1)+Fib(n-2);
}

此时，计算这里的时间复杂度：O(2^n)。
这里，假设求Fib(6);如图所示：

Fil(6)如图，再多进行几次画图我们不难发现它满足等比数列前n项：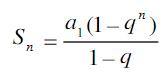
我们利用等比数列公式推出他的Fib(n)的计算次数为2^n-1。从图中，我们可以看出他在计算过程中重复次数过多。
这里如何进行优化呢？
a.利用for()循环

unsigned long long Fib(int n){//相当于于青蛙跳台阶解法
	long long first = 1;
	long long second = 1;
	long long ret = 0;
	for (int i = 3; i <= n; i++){
		ret = first + second;
		first = second;
		second = ret;
	}
	return ret;
}

此时他的时间复杂度为O(n)，空间复杂度为O(1)。
b.动态开辟，利用数组进行存储

long long Fib(int n){
	long long* p = (long long*)malloc(sizeof(long long)*n);
	assert(p != NULL);
	p[0] = 1;
	p[1] = 1;
	for (int i = 2; i<n; ++i){
		p[i] = p[i - 1] + p[i - 2];
	}
	long long x = p[n - 1];
	free(p);
	p = NULL;
	return x;
}

时间复杂度为O(n),空间复杂度为O(n)。
此时，能用递归的方式优化到O(n)吗？
尾递归

long long Fib(int n,long long res,long long rres){//要求递归的数,上一次计算得到的数，上上一次计算得到的数；这里初始赋值应该为res=1;rres=1;相当于斐波那契额数列的第二项和第一项
	//尾递归
	if (n <= 2) return res;
	else return Fib(n - 1, res + rres, res);//这里进行递归，res=res+rres; rres=res;这里的思想和上面的循环差不多
}
int main(){
	int n = 5;
	long long x=Fib(n,1,1);
	cout << x<<endl;
}

此时他的时间复杂度为O(n),空间复杂度为O(1)。
计算结果：

2.空间复杂度

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法。
递归算法空间复杂度：单次需要的空间递归的深度*
递归的深度：在真个递归调用时，空间累积了多少个
注意：栈空间有固定大小的–>函数递归调用的深度不能太深