算法分析(渐进分析）

Posted 2021-06-24 jtwty

目录

• • 一.T(n)函数
  • 二.渐进分析
  • • （1）渐进紧确界（θ记号）
    • • 举例
    • （2）渐进上界 （O记号）
    • • 举例
    • （3）渐进下界 （Ω记号）
    • • 举例
  • 三.常用的换算公式

---

算法分析分为算法时间复杂度分析与算法空间复杂度分析。一般而言，时间对于我们来说更重要，算法的优化主要也是对时间的优化，而对于空间只要我们的计算机性能较好，对于计算结果影响就不会很大。，下面主要也是对算法一些关于时间复杂度的描述！

---

一.T(n)函数

当算法时间仅依赖于问题输入规模n，我们可以将其表示为T(n)。

T(n)直接由每一步的操作次数之和相加构成。

下面我们以插入排序的伪代码为例来计算它的T(n)

但是因为当规模变大时，其主要决定作用的就是最高项，所以我们只需要取它的最高项即可，那么久可以表示为 T(n) = n²

二.渐进分析

渐进分析： 就是指忽略掉T(n)的系数与低阶项，仅关注高阶项，用记号θ表示。

下面我们介绍一些渐进记号：

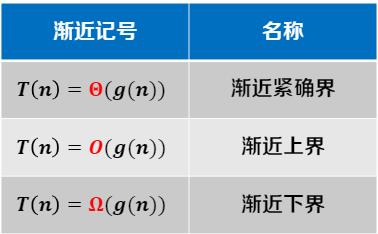
（1）渐进紧确界（θ记号）

先给出它的官方定义：

什么意思呢？就是用θ(g(n))来描述T(n)有一个具体的上界和一个具体的下界，当我们可以找到时，才能进行θ表示。

举例

$$T(n)=\frac{3}{2}{n}^2+\frac{7}{2}-4=\theta (n^2)$$

令n₀ = 2，那么当 n ≥ n₀时，有

寻找下界： $$\frac{3}{2}{n}^2+\frac{7}{2}-4\ge \frac{3}{2}{n}^2\ge n^2$$

寻找上界：$$\frac{3}{2}{n}^2+\frac{7}{2}-4\le \frac{3}{2}{n}^2+\frac{7}{2}+n^2=6n^2$$

所以存在 c₁ = 1，c₂ = 6，n₀ = 2，使得上式成立，存在渐进紧确界，才可以使用 θ(n²) 表示。

同理可得：

$$\frac{3}{2}{n}^5+\frac{7}{2}n-10=\theta (n^5)$$

$$n^3+n^2+n=\theta (n^3)$$

（2）渐进上界 （O记号）

渐进上界使我们算法分析最常用的方式，因为当我们评价一个算法的优劣时，一般都去找它的最差情况，那么这个就是渐进上界。（大O记法）

先看定义：

举例

$$cosn=O(1)$$

因为 cos n 最大取1，所以是O(1)。

$$\frac{n^2}{2}-12n=O(n^2)$$

通过画坐标图来看，很明显 n₂ 更大，所以上界为O(n)。

$$lo{g}_{7}n=\frac{lo{g}_{2}n}{lo{g}_{2}7}=O(lo{g}_{2}n)=O(logn)$$

使用换底公式进行求解。

对于一般的式子来说我们只需要去掉系数取最高项即可，对于特殊的函数我们才会去找他≤什么。

（3）渐进下界 （Ω记号）

渐进下界就是最好情况，一般不使用它来衡量算法的优劣。

它的定义如下：

举例

$$n^3-2n=\Omega (n^3)$$

$$n^2+n=\Omega (n^2)$$

同理对于普通的式子，直接去掉系数取最高阶项，遇到复杂的例如调和级数等，我们才会去找他≥什么。

三.常用的换算公式

O ( f ( n ) ) + O ( g ( n ) ) = O ( m a x { f ( n ) , g ( n ) } ) O(f(n)) + O(g(n)) = O(max \\left \\{f(n),g(n)\\right \\}) O(f(n))+O(g(n))=O(max{f(n),g(n)})

$$O(f(n))+O(g(n))=O(f(n)+g(n))$$

$$O(f(n))\ast O(g(n))=O(f(n)\ast g(n))$$

$$O(c\ast f(n))=O(f(n))$$