有符号数的三种表示：原码反码与补码

Posted howard2005

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了有符号数的三种表示：原码反码与补码相关的知识，希望对你有一定的参考价值。

文章目录

一、计算机中的二进制数表示

（一）数的表示方法

1、定点数

  • 定点数包括定点整数与定点小数
  • 采用定点数的缺点
    ① 编程时需要确定小数点位置
    ② 难以表示两个大小相差较大的数
    ③ 存储空间利用率低

2、浮点数

（1）浮点数概念

  • 小数点的位置可以左右移动的数

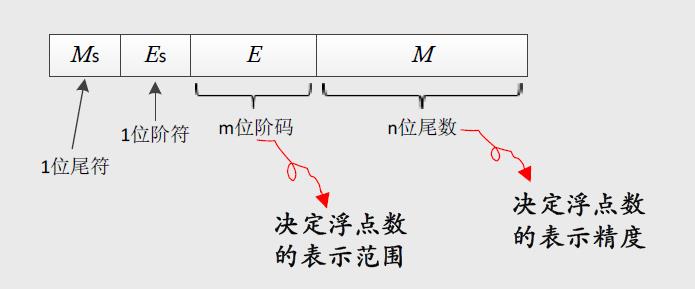
（2）规格化浮点数

  • 尾数部分用纯小数表示，即小数点右边第1位不为0

（二）数的性质

1、无符号数

  • 数中所有的0和1都是数据本身
  • 各种编码多视为无符号数

2、有符号数

  • 需用0或1表示数的性质（整数）
  • 数值多视为有符号数

3、数的性质由设计者决定

  • 在低级语言程序设计中，根据数的性质由程序语言处理（按无符号数或有符号数处理）。

二、无符号数

（一）无符号数的加法

  • 0 + 0 = 0，0 + 1 = 1 ，1 + 0 = 1， 1 + 1 = 0（有进位）

（二）无符号数的减法

  • 0 - 0 = 0，0 - 1 = 1（有借位） 1 - 0 = 1，1 - 1 = 0

（三）无符号数的乘法

  • 0 × 0 = 0　0 × 1 = 0，1 × 0 = 0，1 × 1 = 1

（四）无符号数的除法

  • 0 ÷ 0 = 0，0 ÷ 1 = 0，1 ÷ 0 = 0 （无意义），1 ÷ 1 = 1

（五）乘除法案例演示

  • 乘法：00001011 × 0100 = 00101100B
  • 除法：00001011 ÷ 0100 = 00000010B
    – 商 = 00000010B
    – 余数 = 11B
  • 每乘以2，相对于被乘数向左移动1位
  • 每除以2，相对于被除数向右移动1位

三、有符号数

（一）概念

  • 用最高位表示符号，其余是数值
  • 0：表示正数
  • 1：表示负数

（二）表示方法

1、原码

（1）概念

  • 最高位为符号位，其余为真值部分
  • [ X ] 原 = 符 号 位 + ∣ 绝 对 值 ∣ [X]_原=符号位+|绝对值| [X]原​=符号位+∣绝对值∣

（2）优点

  • 真值和其原码表示之间的对应关系简单，容易理解

（3）缺点

  • 计算机中用原码进行加减运算比较困难
  • 0的表示不唯一

（4）数0的原码

8位数0的原码：

  • + 0 = 0 0000000 +0 = \\colorboxYellow00000000 +0=0​0000000
  • − 0 = 1 0000000 -0 = \\colorboxYellow10000000 −0=1​0000000

由此可见，数0的原码不唯一。

2、反码

（1）概念

对一个机器数X：

  • 若 X > 0 X>0 X>0 ，则 [ X ] 反 = [ X ] 原 [X]_反=[X]_原 [X]反​=[X]原​
  • 若 X < 0 X<0 X<0， 则 [ X ] 反 = 对 应 原 码 的 符 号 位 不 变 ， 数 值 部 分 按 位 求 反 [X]_反=对应原码的符号位不变，数值部分按位求反 [X]反​=对应原码的符号位不变，数值部分按位求反

（2）案例

例1、-52的反码

X = − 52 = − 0110100 X = -52 = -0110100 X=−52=−0110100

  • [ X ] 原 = 1 0110100 [X]_原=\\colorboxyellow10110100 [X]原​=1​0110100
  • [ X ] 反 = 1 1001011 [X]_反=\\colorboxyellow11001011 [X]反​=1​1001011
例2、0的反码
  • [ + 0 ] 反 = [ + 0 ] 原 = 0 0000000 [+0]_反= [+0]_原= \\colorboxyellow00000000 [+0]反​=[+0]原​=0​0000000
  • [ − 0 ] 原 = 1 0000000 [-0]_原= \\colorboxyellow10000000 [−0]原​=1​0000000
  • [ − 0 ] 反 = 1 1111111 [-0]_反 = \\colorboxyellow11111111 [−0]反​=1​1111111

由此可见，数0的反码也不是唯一的。

3、补码

（1）概念

对于机器数X：

  • 若 X > 0 ， 则 [ X ] 补 = [ X ] 反 = [ X ] 原 若X>0， 则[X]_补= [X]_反= [X]_原 若X>0，则[X]补​=[X]反​=[X]原​
  • 若 X < 0 ， 则 [ X ] 补 = [ X ] 反 + 1 若X<0， 则[X]_补= [X]_反+1 若X<0，则[X]补​=[X]反​+1

（2）案例

例1、-52的补码

X = – 52 = – 0110100 X= – 52= – 0110100 X=–52=–0110100

  • [ X ] 原 = 1 0110100 [X]_原=\\colorboxyellow10110100 [X]原​=1​0110100
  • [ X ] 反 = 1 1001011 [X]_反=\\colorboxyellow11001011 [X]反​=1​1001011
  • [ X ] 补 = [ X ] 反 + 1 = 1 1001100 [X]_补= [X]_反+1=\\colorboxyellow11001100 [X]补​=[X]反​+1=1​1001100
例2、0的补码
  • [ + 0 ] 补 = [ + 0 ] 原 = 0 0000000 [+0]_补= [+0]_原=\\colorboxyellow00000000 [+0]补​=[+0]原​=0​0000000
  • [ − 0 ] 补 = [ − 0 ] 反 + 1 = 1 1111111 + 1 = 1 0 0000000 = 0 0000000 [-0]补= [-0]_反+1=\\colorboxyellow11111111+1 =\\colorboxred1\\colorboxyellow00000000=\\colorboxyellow00000000 [−0]补=[−0]反​+1=1​1111111+1=1​0​0000000=0​0000000
  • 说明：对8位字长，进位（红色1）被舍掉
例3、钟表案例 - 将指针从5点拨到1点

两钟拨法：