算法珠玑单源最短路径问题

Posted 2021-04-28 西邮红色青春阵地

单源最短路径问题

什么是单源最短路径问题？

已知一个带权重的有向图G=(V,E) 和权重函数 ω:E→R （该权重函数将有向图中的每条边）映射他的权重。图中任一路径 p= <v0,v1,…,vk› 的长度就是构成该路径所有边的权重之和： 

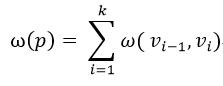
那么从结点u到结点 v的最短路径δ(u,v)被定义为： 

最短路径的变体

• 单目的地最短路径问题

即找到从每个节点u到给定目的地结点t的最短路径。可以将图的每个边翻转，即化为了单源最短路径问题。

• 单结点对最短路径问题

即找到从给定结点 u到给定结点 v的最短路径。在解决结点u或者结点v的单源最短路径问题时，自然而然的解决了这个问题。

最短路径的最优子结构

最短路径算法通常依赖最短路径的一个重要性质：两个结点之间的一条最短路径包含着其他的最短路径。

解决问题需要的算法基础

• 最短路径估计

对于每个节点v而言，我们维持一个属性v.d，用来记录从源节点s到该节点的最短路径的上界。称v.d为s到v的最短路径估计。 

除此之外，我们还维护一个属性v.π，用于指向从源节点到达该节点的最短路径上的前一个节点。 

一般使用以下时间复杂度为Θ(V)的算法来对最短路径估计和前驱节点进行初始化:

INITIALIZE-SINGLE-SOURCE(G, S)

    for each vertex v in G.V 

        v.d = INFINITY

        v.π = NIL

    s.d = 0

• 松弛 Relaxation

松弛操作，即试图降低某一点的最短路径估计并更新他的前驱属性π。

 

具体过程是：将结点s到结点u之间的最短路径最短路径加上u到v之间的权重，并与之前的最短路径估计进行比较,若前者更小，则对v.d和v.π进行更新。 

一般使用以下代码进行：

RELAX(u, v, ω)

    if v.d > u.d + ω(u, v) then

        v.d = u.d + ω(u, v)

        v.π = u

Bellman-Ford算法

该算法可以解决一般情况下单源最短路径问题，而且边的权重可以是负值。算法将返回一个布尔值，用于表示是否存在一个从源节点可以到达的权重为负值的环路。

BELLMAN-FORD(G, ω, s)

    INITIALIZE-SINGLE-SOURCE(G, s)

    for i = 1 to |G.V| - 1

        for each edge<u, v> in G.E

            Relax(u, v, ω)

    for each edge<u, v> in G.E

        if v.d > u.d + ω(u, v) then

            return false

    return true

我们可以看到，该算法的时间复杂度为O(VE)