数据结构—— 图：最短路径问题

Posted 2021-06-23 大彤小忆

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构—— 图：最短路径问题相关的知识，希望对你有一定的参考价值。

3. 最短路径问题

3. 最短路径问题

3.1 最短路径问题的抽象

在网络中，求两个不同顶点之间的所有路径中，边的权值之和最小的那一条路径：
$\\diamond$ 这条路径就是两点之间的最短路径（shortestPath)
$\\diamond$ 第一个顶点为源点（Source)
$\\diamond$ 最后一个顶点为终点(Destination)

3.2 问题分类

单源最短路径问题： 从某固定源点出发，求其到所有其他顶点的最短路径。
$\\diamond$ (有向）无权图
$\\diamond$ (有向）有权图
多源最短路径问题： 求任意两顶点间的最短路径。

3.3 单源最短路算法

3.3.1 无权图的单源最短路算法

按照递增（非递减）的顺序找出各个顶点的最短路。

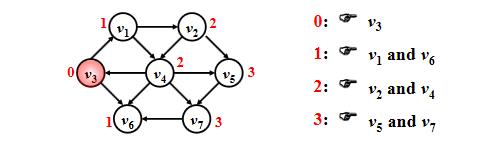
在这里插入图片描述
在数据结构（四）图 —— 编程作业 02 ：Saving James Bond中，James Bond从孤岛跳上岸，最少需要跳多少步?
可以使用BFS算法计算！

BFS算法的代码如下所示。

void BFS(Vertex S)
{ 
    visited[S] = true ;
    Enqueue (S, Q);
    while(!IsEmpty(Q)){
        V = Dequeue (Q);
        for (V的每个邻接点W)
            if (!visited[W]){
                visited[W] = true;
                Enqueue (W, Q);
            }
    }
}

dist[W] = S到W的最短距离
dist[S] = 0
path[W] = S到W的路上经过的某顶点

无权图的单源最短路算法的代码如下所示。

void Unweighted(Vertex S){
    Enqueue (S, Q);
    while(!IsEmpty(Q)){
        V = Dequeue (Q);
        for(V的每个临界点W)
            if (dist[W] == -1){
                dist[W] = dist[V] + 1; // 当前距离上一距离+1
                path[W] = V;  // S到W的必经顶点就是前一个顶点V
                Enqueue (W, Q);
        }
    }
}

时间复杂度为 $T = O (∣ V ∣ + ∣ E ∣)$ 。

3.3.2 有权图的单源最短路算法

在这里插入图片描述
按照递增的顺序找出各个顶点的最短路。

Dijkstra算法： 1. 令S={源点s ＋已经确定了最短路径的顶点 $v_{i}$ }；
2. 对任一未收录的顶点v，定义dist[v]为s到v的最短路径长度，但该路径仅经过S中的顶点。即路径{ s→( $v_{i}∈S$ )→v }的最小长度；
3. 若路径是按照递增（非递减)的顺序生成的，则
$\\diamond$ 真正的最短路必须只经过S中的顶点（为什么?)
$\\diamond$ 每次从未收录的顶点中选一个dist最小的收录（贪心)
$\\diamond$ 增加一个v进入S，可能影响另外一个w的dist值!
$\\circ$ dist[w] = min{dist[w], dist[v] +<v ,w>的权重}

有权图的单源最短路算法的代码如下所示。

void Dijkstra(Vrtex s)
{ 
    while (1){
        V = 未收录顶点中dist最小者;
        if (这样的V不存在)
            break;
        collected[V] == true;
        for (V的每个邻接点W)
            if (collected[W]== false)
                if (dist[V]+E<v,w> < dist[W])
                {
                    dist[W] = dist[V]+ E<v,w>;
                    path[W] = V;
                }
    }
}
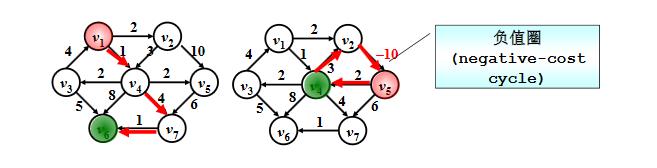
/*不能解决有负边的情况*/

■ 方法1： 直接扫描所有未收录顶点—— $O (∣ V ∣)$
$\\star$ $T=O(|V|^{2}+|E|)$
$\\star$ 对于稠密图效果好
■ 方法2： 将dist存在最小堆中—— $O (l o g ∣ V ∣)$
$\\star$ 更新dist[w]的值—— $O (l o g ∣ V ∣)$
$\\star$ $T = O (∣ V ∣ l o g ∣ V ∣ ＋ ∣ E ∣ l o g ∣ V ∣) = O (∣ E ∣ I o g ∣ V ∣)$
$\\star$ 对于稀疏图效果好

Dijkstra算法的步骤：

step1：初始化所有dist为 $\\infty$ ，初始化所有path为-1；

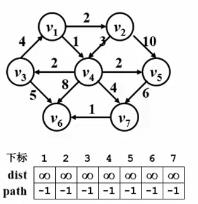
在这里插入图片描述

step2：从顶点 $v_{1}$ 开始，寻找邻接点，更新 $v_{2}$ 和 $v_{4}$ 的dist和path；

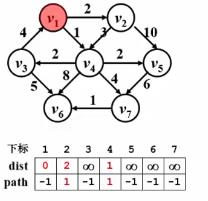
在这里插入图片描述

step3：找到与 $v_{1}$ 最近的邻接点（即dist最小） $v_{4}$ ，标记collected[ $v_{4}$ ]=true，并对 $v_{4}$ 继续寻找邻接点，更新 $v_{3}$ 、 $v_{5}$ 、 $v_{6}$ 和 $v_{7}$ 的dist和path；

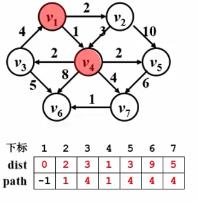
在这里插入图片描述

step4：继续在未收录定点中寻找dist最小的顶点 $v_{2}$ ，标记collected[ $v_{2}$ ]=true，并对 $v_{2}$ 继续寻找邻接点，对于 $v_{2}$ 的邻接点 $v_{5}$ ，若以 $v_{2}$ 为前一个顶点，dist[ $v_{5}$ ]=2+10=12>3，所以不更新 $v_{5}$ 的dist和path；

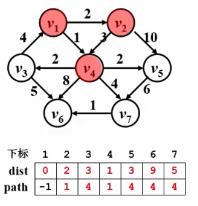
在这里插入图片描述

step5：继续在未收录定点中寻找dist最小的顶点 $v_{3}$ ，标记collected[ $v_{3}$ ]=true，并对 $v_{3}$ 继续寻找邻接点，对于 $v_{3}$ 的邻接点 $v_{6}$ ，由于若以 $v_{3}$ 为前一个顶点，dist[ $v_{6}$ ]=3+5=8<9，所以更新 $v_{6}$ 的dist和path；

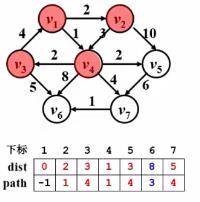
在这里插入图片描述

step6：继续在未收录定点中寻找dist最小的顶点 $v_{5}$ ，标记collected[ $v_{5}$ ]=true，并对 $v_{5}$ 继续寻找邻接点，对于 $v_{5}$ 的邻接点 $v_{7}$ ，若以 $v_{5}$