图文解析 Dijkstra单源最短路径算法

Posted 2023-05-17

参考技术A 给定 加权有向图 G=(V,E,W)，每条边的权值w为 非负数 ，表示两个顶点间的距离。

源点s∈V。

求：从s出发到其他各个顶点的最短路径。

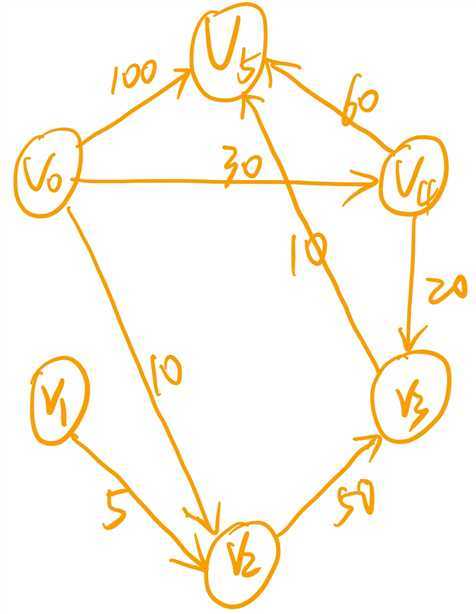
如上图所示，以1为源点，计算到其余各个顶点的最短距离（我已用红线标出）。下面列出了最终解：

S集合 ：当从s到x（x ∈V ）的最短路径找到时，则x ∈S。当所有顶点都进入S集合时，算法结束。

初始：S=｛s｝，当S=V时算法结束。

从s到u相对于S的最短路径 ：指从s到u且仅经过S中顶点的最短路径。

dist[u]:从s到u相对于S的最短路径长度

short[u]:从s到u最短路径的长度（算法最终解）

dist[u] ≥ short[u]

Dijkstra算法采用贪心算法模式，算法过程就是通过计算dist[u],不断扩充S集合，同时dist[u]会不断优化改善，直到dist[u] = short[u]，并将其放到S中，当所有顶点都放入S集合时，算法结束。

输入：加权有向图G=(V,E,W)

          V=1,2,…,n, s=1

输出：从s到每个顶点的最短路径

输入：G=(V,E,W)，源点1

          V=1,2,3,4,5,6

初始S集合只有1，计算直接从1能到达的顶点的距离，其他不能从1号顶点直接到达的顶点都记为无穷大。此时从dist[u]里找出最短距离的顶点（6号），并将其放进S集合。

  S=1

  dist[1] = 0

  dist[2] = 10

  dist[6 ] = 3

  dist[3] = ∞

  dist[4] = ∞

  dist[5] = ∞

当把6号顶点放进S集合后，经由6号顶点出发到达的顶点的最短距离可能会被优化更新，因为该算法的思想很“贪心”，谁更短我要谁！比如1->6->2要比1->2距离更短，所以dist[2]被更新为5，从专业术语上讲，这个“更新”过程叫做松弛，其他点同理。然后从dist[u]里找出最短的路径的那个顶点（5号），并放进S集合里。

  S=1,6

  dist[1] = 0

 dist[6] = 3

  dist[2] = 5

  dist[4] = 9

  dist[5] = 4

  dist[3] = ∞

后面的操作步骤其实就是重复上面的操作。即当S集合里有个新的顶点后，就可能会更新其他点的最短距离，更新一遍后，找出当前最短距离的dist[u]，并将该顶点放进S集合。后面不重复阐述。

  S=1,6,5

  dist[1] = 0

 dist[6] = 3

  dist[5] = 4

  dist[2] = 5

  dist[4] = 9

  dist[3] = ∞

  S=1,6,5,2

  dist[1] = 0

 dist[6] = 3

  dist[5] = 4

 dist[2] = 5

  dist[4] = 9

  dist[3] = 12

  S=1,6,5,2,4

  dist[1] = 0

 dist[6] = 3

  dist[5] = 4

 dist[2] = 5

 dist[4] = 9

  dist[3] = 12

  S=1,6,5,2,4,3

  dist[1] = 0

 dist[6] = 3

  dist[5] = 4

 dist[2] = 5

 dist[4] = 9

 dist[3] = 12

当有向图中的所有顶点都进入了S集合后，算法结束，此时的dist[u]的值其实就是最初我们找出的那个最终解short[u]，所以，算法结束时，dist[u]=short[u],得到最终解。

[C++]单源最短路径：迪杰斯特拉(Dijkstra)算法(贪心算法)

1 Dijkstra算法

1.1 算法基本信息

• 解决问题/提出背景
  • 单源最短路径（在带权有向图中，求从某顶点到其余各顶点的最短路径）
• 算法思想
  • 贪心算法
    • 按路径长度递增的次序，依次产生最短路径的算法
  • 【适用范围】Dijkstra算法仅适用于【权重为正】的图模型中
• 时间复杂度
  • O(n^3)
• 补充说明
  • 亦可应用于【多源最短路径】(推荐：Floyd算法(动态规划,O(n^3)))

    • Dijkstra 时间复杂度：O(n^3)

      1.2 算法描述

• 1.2.1 求解过程(具体思路)

• 1.2.2 示例

1.2 编程复现

• 1> 定义图模型(邻接矩阵表示法)的【基本存储结构体】

# define MaxInt 32767 // 表示极大值 即 ∞ (无穷大)
# define MVNum 100 // 最大顶点数 

typedef int VertexType; // 假设顶点的数据类型为整型

typedef int ArcType; // 假设Vi与Vj之边的权值类型为整型 

typedef struct 
    VertexType vexs[MVNum]; // 顶点表 (存储顶点信息)
    ArcType arcs[MVNum][MVNum]; // 邻接矩阵
    int vexnum,arcnum; // 图的当前顶点数与边数 
AMGraph; // Adjacent Matrix Graph 邻接矩阵图 

• 2> 定义 Dijkstra 算法的【辅助数据结构体】

bool S[MVNum]; // S[i] 记录从源点V0到终点Vi是否已被确定为最短路径长度  【划分确定与未确定: 跟贪心算法的适用范围(不可取消性)有直接联系】
               // true：表已确定；false：表尚未确定
ArcType D[MVNum]; // D[i] 记录从源点V0到终点Vi的【当前】最短路径【长度】 
int Path[MVNum];  // Path[i] 记录从源点V0到终点Vi的【当前】最短路径上【Vi的[直接前驱]的顶点序号】 

• 3> 初始化(邻接矩阵)带权有向图的图模型

void InitAMGraph(AMGraph &G)
    cout<<"Please Input Vertexs Number:";
    cin>>G.vexnum;
    cout<<"\\nPlease Directed Edges Number:";
    cin>>G.arcnum;
    
    for(int i=0;i<MVNum;i++)
        for(int j=0;j<MVNum;j++)
            if(i!=j) // 【易错】 初始化<Vi, Vj>时: <Vi,Vj> 路径长度无穷大 (i!=j) 
                G.arcs[i][j] = MaxInt;
             else  //  【易错】 初始化<Vi, Vj>时: <Vi,Vi>【自回环】路径长度为0 (i==i) 
                G.arcs[i][j] = 0;
            
        
    
    for(int i=0;i<G.vexnum;i++)
        G.vexs[i] = i;
    
    cout<<"\\nPlease Input All Directed Edges and their Weight now:";
    cout<<"\\nDirected Edges(i,j,weight): "<<endl;
    int i,j;
    int weight;
    for(int k=0;k<G.arcnum;k++)
//      cout<<"("<<(k+1)<<") ";
        cin>>i;cin>>j;cin>>weight;
        G.arcs[i][j] = weight;
    
    cout<<endl;

• 4> Dijkstra算法：求解单源最短路径

void ShortestPath_Dijkstra(AMGraph G, int V0)
    //step1 n个顶点依次初始化
    int n =G.vexnum;  
    for(int v=0;v<n;v++)
        S[v] = false;
        D[v] = G.arcs[V0][v];
        if(D[v]<MaxInt)
            Path[v] = V0;
         else 
            Path[v] = -1;
        
    
    //step2 将源点V0划入已确定集合S中 
    S[V0] = true;
    D[V0] = 0; // 源点V0到源点V0的最短路径长度必然为0
    //step3 贪心算法策略：
    //          3.1 循环遍历所有结点：
    //              3.2 先确定当前最短路径的终点v；
    //              3.3 然后，将v划入已确定集合S中；
    //              3.4 最后，以利用结点v更新所有尚未确定的结点的最短路径
    int v;
    int min;
    D[G.vexnum] = MaxInt;
    for(int i=1;i<n;i++)//3.1循环遍历所有结点 （即 求从源点V0到图中每一顶点(共计n-1个顶点)的最短路径） 
        //3.2 确定当前最短路径的终点v；
        min = MaxInt;
        for(int w=0;w<n;w++)
            if(S[w]==false && D[w]<min)//比本轮循环中，已知的最短路径还短 【易错/易漏】 S[w]==false ： 必须满足当前结点 Vw 属于尚未确定的结点 
                v = w;
                min = D[w];
            
        
        //3.3 然后，将v划入已确定集合S中；
        S[v] = true;
        //3.4 最后，以利用结点v更新所有尚未确定的结点的最短路径
        for(int w=0;w<n;w++)
            //↓更新Vw结点的最短路径长度为 D[v] + G.arcs[v][w] 
            //cout<<"S["<<w<<"]:"<<S[w]<<"D["<<v<<"]"<<D[v]<<"G.arcs["<<v<<"]["<<w<<"]"<<"D["<<w<<"]"<<D[w]<<endl; 
            if(S[w]==false && (D[v] + G.arcs[v][w] < D[w]))//【易错/易漏】 S[w]==false ： 必须满足当前结点 Vw 属于尚未确定的结点 
                D[w] = D[v] + G.arcs[v][w];
                Path[w] = v; // 更新 结点Vw的前驱为 v 
            
        
        v = G.vexnum;
     

• 5> 输出结果 D[i]、Path[j]

void OutputD(AMGraph G, int V0)
    cout<<"Shortest Distance Weight of the Pair of Directed Vertices("<<V0<<", j):"<<endl; 
    for(int j=0;j<G.vexnum;j++)
        cout<<D[j]<<"\\t"; 
    
    cout<<endl;


void OutputPath(AMGraph G,int V0)
    cout<<"Shortest Distance Path("<<V0<<",j) of the Pair of Directed Vertices:"<<endl; 
    for(int j=0;j<G.vexnum;j++)
        cout<<Path[j]<<"\\t"; 
    
    cout<<endl;

• 6> 执行：Main函数

int main()
    int V0; //源点V0的下标 
    AMGraph G;
    InitAMGraph(G);
    
    cout<<"Please Input the Index of Source Node 'V0':";
    cin>>V0;
    ShortestPath_Dijkstra(G, V0);
    OutputD(G, V0);
    OutputPath(G, V0);
    return 0;

• 7> Test: Output of Main

Please Input Vertexs Number:6

Please Directed Edges Number:8

Please Input All Directed Edges and their Weight now:
Directed Edges(i,j,weight):
1 2 5
0 2 10
3 5 10
4 3 20
0 4 30
2 3 50
4 5 60
0 5 100

Please Input the Index of Source Node 'V0':0

Shortest Distance Weight of the Pair of Directed Vertices(0, j):
0       32767   10      50      30      60

Shortest Distance Path(0,j) of the Pair of Directed Vertices:
0       -1      0       4       0       3

2 参考文献

• 《数据结构(C语言版/ 严蔚敏 李冬梅 吴伟民 编)》