动态规划-96. 不同的二叉搜索树

Posted 2021-04-18 大树的编程之旅

点击蓝字关注我，一起成长

1

题目

给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

2

样例

3

样例解读

首先是理解何为二叉搜索树：

二叉搜索树（又：二叉查找树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉排序树。

可得：

（1）由1 - n 都能够作为根结点构成二叉搜索树！
（2）二叉搜索树的根结点的左右子树都是二叉搜索树！

拿到题目的第一想法：画图！于是我们可以得到：

n == 1以及 n == 2的情况如下：

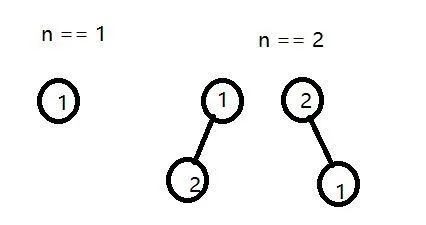
由上可以看出，n == 2的时候，作为根结点有两种选择，一种是1，一种是2；

当 n = 3时：

结合上面对二叉搜索树的分析，我们发现：

假设根结点是 i （1 <= i <= n），可得：

左子树由 [ 1, i - 1]构成，右子树由 [ i + 1, n] 构成！

而且左右子树的结构都是二叉搜索树，那么相当于右子树[ i + 1, n] 如果只看结构的话，也会跟 [1 , n - i ] 的结构相同，所以我们可以得到：

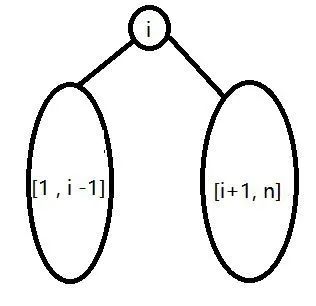
当前以 i 为根结点的二叉搜索树的种类有：

root[i] = root[i - 1] * root[n - i ] ;//左右子树的种类相乘

求1 - n 所能够组合成的二叉搜索树的总种类数为：

dp[n] = root[1] + root[2] + ...... + root[n];

其中 dp[1] = root[1] = 1;

4

解答与代码

答案：

class Solution { public int numTrees(int n) { int[] dp = new int[n+1]; dp[0] = 1; dp[1] = 1; for(int i=2;i<=n;i++){ if(i % 2 != 0){ // 3/2 = 1,需要手动计算2即是中间这一个 for(int j = 1;j <= i/2;j++){ dp[i] += dp[i - j] * dp[j - 1]; //是两边相乘 } //先翻倍 dp[i] *= 2; //计算中间值 dp[i] += dp[i - (i / 2 + 1)] * dp[i / 2 ]; }else{ for(int j = 1;j <= i/2;j++){ dp[i] += dp[i - j] * dp[j - 1]; } //翻倍 dp[i] *= 2; } } return dp[n]; }}

‍

5

预告

下次专题：位运算

明天预告题目：1290. 二进制链表转整数

● 扫码关注我

题目素材来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/unique-binary-search-trees/

喜欢我们的内容就点“在看”分享给小伙伴哦