二叉树遍历就是这么简单(必杀)

Posted 2021-04-09 机智的程序员小熊

喜欢我的文章，点击上方“ 编程三分钟 ”关注，不加班时更新。

回复“资源”，获取一份专属大礼包。

真爱，加个“星标” 或者点个“在看”。

这一篇文章是来自故里的投稿，小熊做了部分修改，编程大队人才辈出。

标语：学习就是个不断搬砖和不断复习的过程，少数强者可以创新，多数人逐渐将其遗忘。

小编带大家学习数据结构中的二叉树，我们这里的实现主要是用 C 语言去实现的，当然也有 C++的语法，用基础的语言有助于我们更好理解数据结构。

让我们先看看二叉树长什么样子。

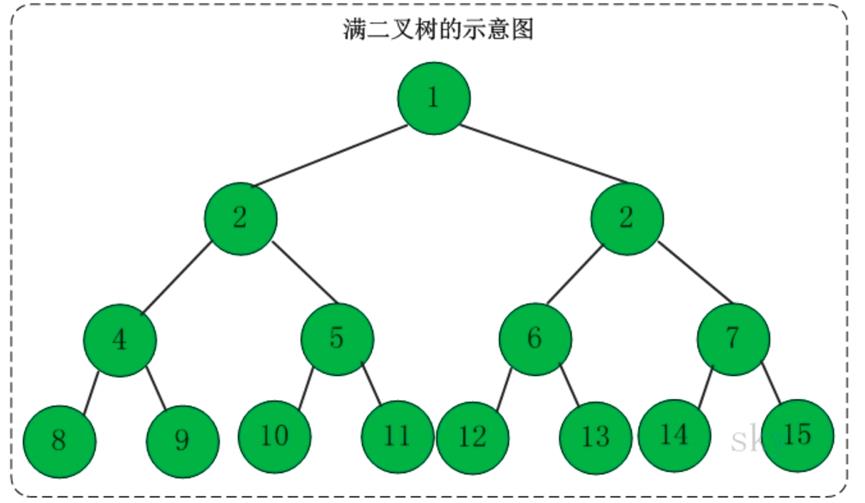
看起来很刺激，不要谎，让我慢慢道来。

线性与非线性

首先我们要知道数据结构中二叉树是个非线性结构，我们了解过数组，顺序表，链表等线性结构。线性结构就是和线性思维类似都是一条路走到黑。

比如女朋友最喜欢问的世纪难题，如果你用线性思维来答题，就只会在固定选项里找答案。

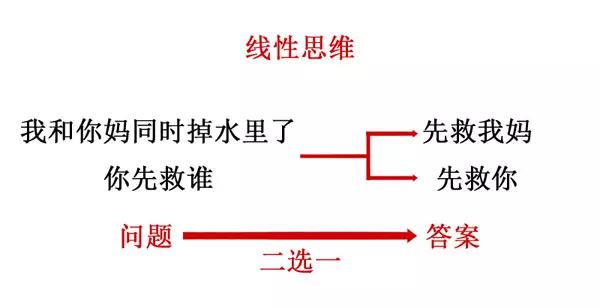
结果肯定是惨烈的，但是你用非线性思维来答题，感觉就瞬间不一样了！

对于计算机而言，只用线性结构存储数据是远远不够的，我们还需要非线性结构来保存，今天所说二叉树就是最简单的一种非线性结构。

什么是二叉树

学习二叉树我们想，为什么叫做二叉树呢？类比树，我们这个结构是不是有树根树杈呢？

那二叉是不是因为每个树干有两个树杈呢？没错！让我们来简单画一堆圈圈和几条线。

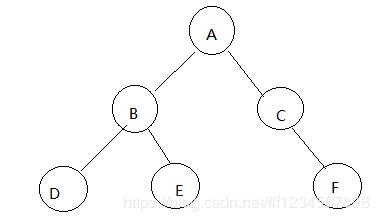
看！上面图里的元素都是自己牛逼的名字，圈圈叫节点，而线就叫 线(我编不下去了。。)，除了根节点之外的节点，也被称为叶子节点，简称叶子。

线是一种关系，代表了节点到节点的指向。

1. 让我们和别人的女朋友一起喝一杯 拿铁，然后创建一个节点

typedef struct BinTreeNode
{
	DataType data;
	struct BinTreeNode* LeftChild;
	struct BinTreeNode* RightChild;
}BinTreeNode;//创建节点

这是一个结构体类型，每个节点有三个要素：data 数据，LeftChild 指向左节点的指针，RightChild 指向右节点的指针

是的，就是上图这个鬼样子。是不是像插了两根牙签的饭团。

然后，我们再声明一个二维指针，用来指向树的根节点

BinTreeNode** t;

2. 当这个树雏形出来了后，我们需要做的就是完善这个二叉树，我们需要将这个树初始化和进行一系列的操作；

我们先来看二叉树的创建 ：

我们可以细分成两种方法，第一种返回二叉树根节点指针，另一种是没有返回值的，根节点指针当参数传入，创建完根节点指针就指向了完整的树。

无返回值创建方式

void BinTreeCreat_1(BinTreeNode** t)//记住我们传的是树根的地址，这个**你应该知道了奥
{
	DataType item;
	scanf("%c", &item);
	if (item == '#')
	{
		*t = NULL;
	}
	else
	{
		*t = (BinTreeNode*)malloc(sizeof(BinTreeNode));
		assert(*t != NULL);
		(*t)->data = item;
		BinTreeCreat_1(&((*t)->LeftChild));
		BinTreeCreat_1(&((*t)->RightChild));
	}
}

细心的你可以看到scanf语句，这个就代表输入，这样我们就可以指挥树创建成什么样子啦！我们规定输入#代表空值，也就是上一个节点没有左叶子或者右叶子。

有返回值创建方式

BinTreeNode* BinTreeCreate_2()
{
	DataType item;
	scanf("%c", &item);
	if (item == '#')
	{
		return NULL;
	}
	else
	{
		BinTreeNode* p = (BinTreeNode*)malloc(sizeof(BinTreeNode));
		assert(p != NULL);
		p->data = item;
		p->LeftChild = BinTreeCreate_2();
		p->RightChild = BinTreeCreate_2();
		return p;
	}
}

当然啦，我这里是输入一个数据创建一个节点，你也可以先用个数组来保存这个你输入的值，来创建二叉树。

二叉树的遍历

创建二叉树已经完了，第一次接触的同学可能感觉快要窒息了，赶紧把这篇文章收藏下来慢慢看，休息一下，打一把 王者农药。

还有余力的同学继续随便用上面的方法，创建一棵树。

void BinTreeCreate(BinTree* t)
{
	(*t).root = BinTreeCreate_2();
}

遍历分三种，先序(前序)、中序、后序遍历。

先序遍历

规则：每次优先遍历根节点，口诀：根左右

先序遍历 递归形式

void _PreOrder(BinTreeNode *t)
{
	if (t != NULL)
	{
		printf("%c ", t->data);
		_PreOrder(t->LeftChild);
		_PreOrder(t->RightChild);
	}
}
//调用，t就是根节点指针
PreOrder(*t);

先序遍历 非递归形式

现在要引入一个叫“栈”的数据结构，我们默认你已经知道栈的特性，不知道的同学晚自习下了以后留下来和苍老师好好补补课！！

栈的作用就是记录下来遍历的路径，我们可以用栈代替任何用递归做的事情（考试要考）

取栈顶相当于是退回父节点

//c++中现成的栈
stack <BinTreeNode*> s;

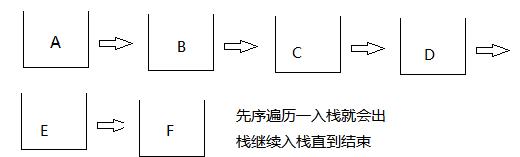
前序遍历，根左右，删除栈顶元素的位置要放对。

来看代码

void PreOrder(BinTree * t)
{
	_PreOrderNoR((*t));
}
void _PreOrderNoR(BinTreeNode *t)
{
	BinTreeNode* p;
	if (t != NULL)
	{
		s.push(t);
		while (!s.empty())
		{
			p = s.top();
			s.pop();
			printf("%c ", p->data);
			if (p->RightChild != NULL)//为啥是这个顺序呢？后进栈的在栈顶
			{
				s.push(p->RightChild);
			}
			if (p->LeftChild != NULL)
			{
				s.push(p->LeftChild);
			}
		}
	}
}

代码看不懂？看看图(橙色代表输出)

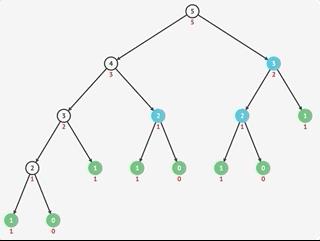
中序遍历

中序遍历 递归形式

这个和前面递归形式一样，不过是换换顺序

void InOrder(BinTreeNode** t)
{
	_InOrder(*t);
}
void _InOrder(BinTreeNode *t)
{
	if (t != NULL)
	{
		_InOrder(t->LeftChild);
		printf("%c ", t->data);
		_InOrder(t->RightChild);
	}
}

中序遍历 非递归形式

中序遍历的时候，非递归的过程就显得容易一点，先将二叉树从根节点到最左边节点都压入栈中，最后一个左节点空，出栈，打印，判断有没有右子树，如果有就将到新的分支中。

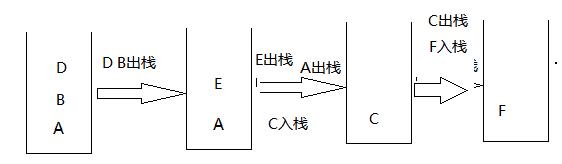
来看代码

void _InOrderNoR(BinTreeNode *t)
{
	BinTreeNode* p;
	stack<BinTreeNode*>dp;
	do
	{
		while (t != NULL)
		{
			dp.push(t);
			t = t->LeftChild;
		}
		p = dp.top();
		dp.pop();
		printf("%c ", p->data);
		if (p->RightChild != NULL)
			t = p->RightChild;
	}while(!dp.empty()||t!=NULL)
}
void InOrderNoR(BinTreeNode** t)
{
	_InOrderNoR((*t));
}

后序遍历

首选还是看递归遍历，可以抢答了！无非就是颠倒一下递归函数位置

void PostOrder(BinTreeNode** t)
{
	_PostOrder((*t));
}
void _PostOrder(BinTreeNode *t)
{
	if (t != NULL)
	{
		_PostOrder(t->LeftChild);
		_PostOrder(t->RightChild);
		printf("%c ", t->data);
	}
}

谈到二叉树的后续遍历，可以说是非递归遍历中最难写也是最难理解的代码了，我们有了对前两个非递归遍历的理解，后续遍历在压栈的时候根节点一定是压在最下层的，怎么实现呢？

先找到最左边的节点，在寻找过程中将遍历的节点压入栈中（不输出），然后依次退节点看有没有右树，最后再取栈顶。

这时候有个问题就是返回上个节点如果是从左子树返回会判断是否有有右子树，那么从右子树返回是不是该到根节点了呢？这两个返回怎么区分从哪返回的呢？这时候就要加个指针作为标志位，这个标志位记录是从哪边返回来的。

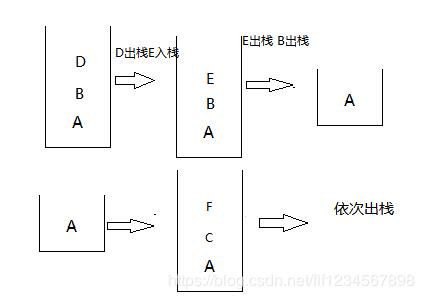
来看代码

void _PostOrderNoR(BinTreeNode *t)
{
	if (t != NULL)
	{
		BinTreeNode*p, *prev = NULL;
		stack<BinTreeNode*> dq;
		do
		{
			while (t != NULL)
			{
				dq.push(t);
				t = t->LeftChild;
			}
			p = dq.top;
			if (p->RightChild == NULL || p->RightChild == prev)
			{
				dq.pop();
				printf("%c ", p->data);
				prev = p;
			}
			else {
				t = p->RightChild;
			}
		} while (!dq.empty());
	}
}
void PostOrderNoR(BinTreeNode** t)
{
	_PostOrderNoR((*t));
}

void PostOrder(BinTreeNode** t)
{
	_PostOrder((*t));
}

这就是数据结构中二叉树的前中后续非递归遍历和递归遍历的写法，递归简化思维，非递归简化计算，看我们怎么去用这些代码实现我们想要的结果。

小编心得：学习这件事情，一辈子不能抛弃，一旦你抛弃了学习，就意味着你选择了平庸。

最后，发起一个长期活动，每15天  留言 最多的人送上一本书或企鹅公仔。

今日问题：你平时在哪里刷算法？

榜单，除去我自己2，3两位同学并列第一，时间还剩下6天

每天发文的第二条留言也算哦

推荐阅读：

如有收获，点个在看，诚挚感谢