人工智能数学基础01--高等数学基础(极限)
Posted 剑威
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了人工智能数学基础01--高等数学基础(极限)相关的知识,希望对你有一定的参考价值。

极限定义
某一个函数中的某一个变量,此变量在变大(或者变小)的永远变化的过程中,逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A ( 永远不能够等于A,但是取等于A 已经足够取得高精度计算结果)的过程中,此变量的变化,被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近A点的趋势”。极限是一种“变化状态”的描述。此变量永远趋近的值A叫做“极限值” 。
数列
按照一定次序排列的一列数: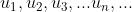 ,其中
,其中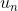 叫做通项。
叫做通项。
对于数列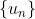 ,如果当 n 无限增大时,其通项无限接近于一个常数A,则称该数列以A为极限,或称数列收敛于A,否则称数列为发散。
,如果当 n 无限增大时,其通项无限接近于一个常数A,则称该数列以A为极限,或称数列收敛于A,否则称数列为发散。
极限符号表示
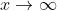 表示:当
表示:当 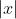 无限增大时;
无限增大时;
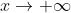 表示:当 x 无限增大时;
表示:当 x 无限增大时;
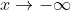 表示:当 x 无限减小时;
表示:当 x 无限减小时;
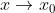 表示:当 x 从
表示:当 x 从 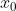 的左右两侧无限接近于
的左右两侧无限接近于 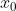 时;
时;
 表示:当 x 从
表示:当 x 从 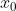 的右侧无限接近于
的右侧无限接近于 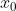 时;
时;
 表示: 当 x 从
表示: 当 x 从 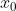 的左侧无限接近于
的左侧无限接近于 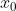 时;
时;
极限存在的两个重要法则
-
夹逼定理
设:
- 在*的去心邻域内
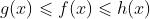 ;
; 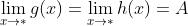
则:
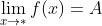
注:
- 夹逼定理对于数列同样成立;
- 上面的A换成
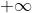 或者
或者 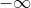 ,定理也成立
,定理也成立
-
单调有界定理
设数列 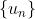 单调增加(减少)且有上(下)界
单调增加(减少)且有上(下)界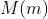 ,则
,则 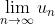 存在,且
存在,且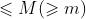 。
。
注:
单调有界定理对函数的极限也成立。
极限运算方法
-
运算法则(四则运算法则)
设: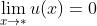
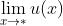 存在且等于 A,
存在且等于 A, 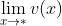 存在且等于B。
存在且等于B。
则:
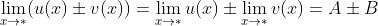 ;
;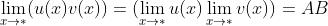 ;
;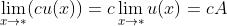 (c为常数);
(c为常数);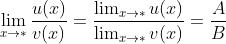 (设
(设 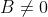 );
); ,并设在* 的去心邻域内
,并设在* 的去心邻域内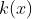 有界,则
有界,则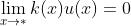 。
。
注:
- 如果
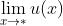 与
与 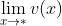 都不存在,那么
都不存在,那么 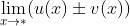 不能写成
不能写成 ;
; - 如果
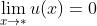 ,
, ,那么求
,那么求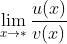 不能用前面公式4.。
不能用前面公式4.。
-
等价无穷小替换与等价无穷小的充要条件
等价无穷小替换定理
设:
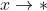 时,
时,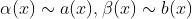
则:
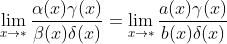
注:
- 上式的含义是,若上式右边存在,则左边等于右边;若上式右边为
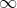 (或其他情形的不存在),则左边亦为
(或其他情形的不存在),则左边亦为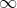 (或其他情形的不存在)。
(或其他情形的不存在)。 - 整个式子中的乘除因子可用等价无穷小替换求其极限,加、减时不能用等价无穷小替换,部分式子的乘除因子也不能用等价无穷小替换。
等价无穷小的充要条件
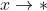 时
时 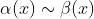 的充要条件是
的充要条件是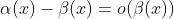 。
。
例如: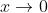 时,
时,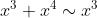 。这是因为
。这是因为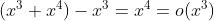 。
。
-
洛必达法则
法则1
设:
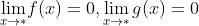 ;
;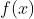 与
与 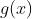 在 * 的去心邻域 U 内可导,且
在 * 的去心邻域 U 内可导,且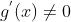 ;
;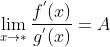 (或
(或 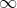 ),
),
则:
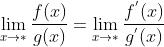
法则2
设:
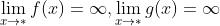 ;
;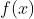 与
与 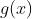 在 * 的去心邻域 U 内可导,且
在 * 的去心邻域 U 内可导,且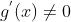 ;
;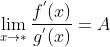 (或
(或 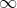 ),
),
则:
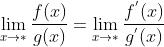
注:
条件1.是必须检查的,不是  型或
型或  型就不能使用洛必达法则。
型就不能使用洛必达法则。
-
佩亚诺余项泰勒公式
设:
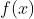 在
在 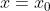 处存在
处存在 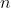 阶导数
阶导数
则:
有公式 
其中
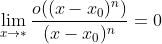 ,该公式称为在
,该公式称为在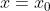 处的具有佩亚诺余项的
处的具有佩亚诺余项的 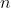 阶泰勒公式,
阶泰勒公式,
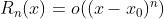 称为佩亚诺余项。
称为佩亚诺余项。
-
利用积分和式求极限公式
设:
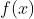 在
在 ![\\left [ 0,1 \\right ]](https://image.cha138.com/20210721/433665d201c8427eb778ca32e9042b42.jpg) 上连续,
上连续, 或
或  ,
,
则:
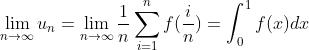 或者
或者 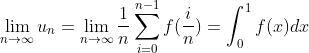 。
。
无穷
无穷小以0为极限,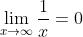 , 则
, 则  是
是 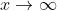 时的无穷小
时的无穷小
无穷小的基本性质:
- 有限个无穷小的代数和仍是无穷小;
- 有限个无穷小的积仍是无穷小;
- 有界变量与无穷小的积仍是无穷小;
- 有限个无穷小之和不一定是无穷小;
- 无穷小的商不一定是无穷小;
- 极限有无穷小的关系:
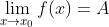 的充要条件
的充要条件  ,其中
,其中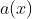 是
是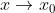 时的无穷小。
时的无穷小。
无穷小的比较:
假设有 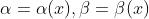 都是无穷小,即:
都是无穷小,即:
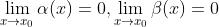
如果 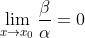 ,则称
,则称 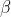 是比
是比 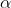 高阶无穷小
高阶无穷小
如果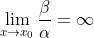 ,则称
,则称 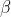 是比
是比 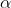 低阶无穷小
低阶无穷小
如果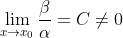 , 则称
, 则称 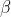 与
与 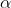 是同阶无穷小
是同阶无穷小
无穷大并不是一个很大的数,时相对于变换过程来说的。
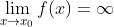 或
或 
无穷大和无穷小的关系:在自变量变换的同一过程中,如果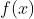 为无穷大,那么
为无穷大,那么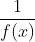 为无穷小
为无穷小
以上是关于人工智能数学基础01--高等数学基础(极限)的主要内容,如果未能解决你的问题,请参考以下文章