人工智能数学基础01--高等数据基础(导数与微分)01
Posted 剑威
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了人工智能数学基础01--高等数据基础(导数与微分)01相关的知识,希望对你有一定的参考价值。

导数
定义:
设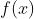 在
在 的某个邻域
的某个邻域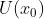 内有定义,并设
内有定义,并设 。
。
如果:
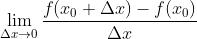 存在,
存在,
则称:
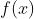 在
在  处可导,并称上述极限为
处可导,并称上述极限为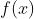 在
在 处的导数
处的导数
记为:
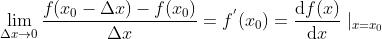
若记 ,则在
,则在 点的导数又可记成
点的导数又可记成 等等。
等等。
如果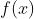 在区间
在区间 内每一点都可导,则称
内每一点都可导,则称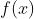 在
在 内可导,
内可导, 称为
称为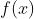 在
在 内的导函数,简称导数。
内的导函数,简称导数。
在定义式中,若记 ,则该式可改写为
,则该式可改写为

注:
导数的定义式中,必须要有 ,并且其中的
,并且其中的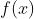 是
是 附近的
附近的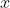 处的函数值,没有这些,就谈不上求导数,在按定义求导数时,必须注意。
处的函数值,没有这些,就谈不上求导数,在按定义求导数时,必须注意。
举例说明
平均速度  ,速度的概念是一个瞬时概念,但如何表示瞬时速度?
,速度的概念是一个瞬时概念,但如何表示瞬时速度?
瞬时经过的路程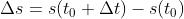 ,那么这一小段的平均速度就是
,那么这一小段的平均速度就是

当 时也就是瞬时的速度了:
时也就是瞬时的速度了:
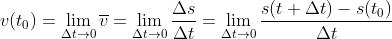
以上是关于人工智能数学基础01--高等数据基础(导数与微分)01的主要内容,如果未能解决你的问题,请参考以下文章