文献阅读19期:SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
Posted RaZLeon
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了文献阅读19期:SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS相关的知识,希望对你有一定的参考价值。
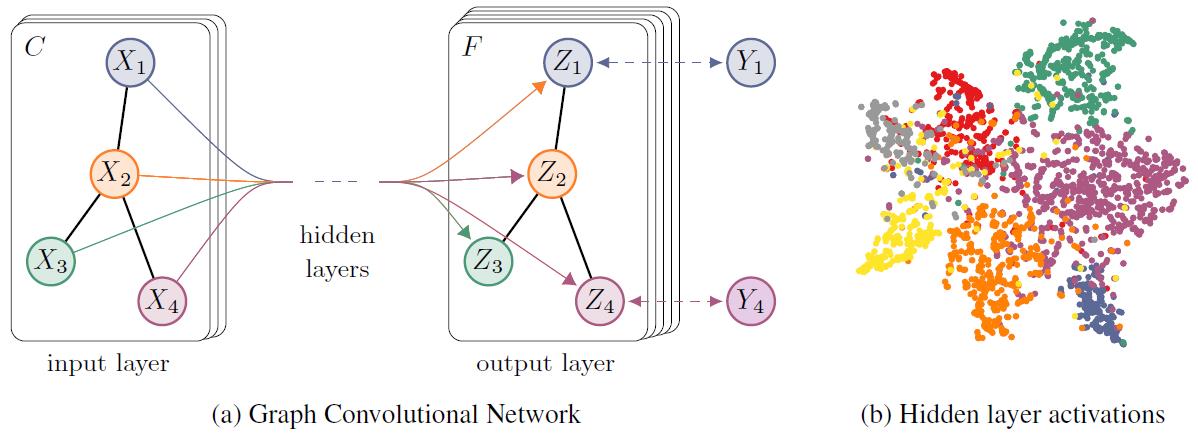
[ 文献阅读·图卷积网络 ] SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS [1]
推荐理由:用巧妙的方法推出层与层之间的传播规则,很好地实现了半监督节点分类。
1.摘要&简介
- 本文的“半监督”,首先体现在损失函数上,加入监督损失的损失函数长这样:
L = L 0 + λ L r e g \\mathcal{L}=\\mathcal{L}_{0}+\\lambda \\mathcal{L}_{\\mathrm{reg}} L=L0+λLreg
其中, L 0 \\mathcal{L}_{0} L0为监督损失项,而 L reg \\mathcal{L}_{\\text {reg }} Lreg 的其具体表达式为:
L reg = ∑ i , j A i j ∥ f ( X i ) − f ( X j ) ∥ 2 = f ( X ) ⊤ Δ f ( X ) \\mathcal{L}_{\\text {reg }}=\\sum_{i, j} A_{i j}\\left\\|f\\left(X_{i}\\right)-f\\left(X_{j}\\right)\\right\\|^{2}=f(X)^{\\top} \\Delta f(X) Lreg =i,j∑Aij∥f(Xi)−f(Xj)∥2=f(X)⊤Δf(X) - 本文的工作有两部分组成:
- 提出一种简单且性能良好的直接作用于图的神经网络模型的逐层传播规则,并展示了如何从谱图卷积的一阶近似中激发它。
- 这种基于图的神经网络模型用于图中节点的快速和可伸缩的半监督分类。
2. 图的快速近似卷积
- 首先来看一下本文的层与层的传播规则:
H ( l + 1 ) = σ ( D ~ − 1 2 A ~ D ~ − 1 2 H ( l ) W ( l ) ) (2) H^{(l+1)}=\\sigma\\left(\\tilde{D}^{-\\frac{1}{2}} \\tilde{A} \\tilde{D}^{-\\frac{1}{2}} H^{(l)} W^{(l)}\\right)\\tag{2} H(l+1)=σ(D~−21A~D~−21H(l)W(l))(2)
其中 A ~ = A + I N \\tilde{A}=A+I_{N} A~=A+IN, D ~ i i = ∑ j A ~ i j \\tilde{D}_{i i}=\\sum_{j} \\tilde{A}_{i j} D~ii=∑jA~ij, H ( 0 ) = X H^{(0)}=X H(0)=X, σ ( ⋅ ) \\sigma(\\cdot) σ(⋅)代表任何激活函数,比如ReLU等等。
2.1.谱图卷积
- 谱图卷积一般定义为信号
x
∈
R
N
x \\in \\mathbb{R}^{N}
x∈RN,与参数为
θ
∈
R
N
\\theta \\in \\mathbb{R}^{N}
θ∈RN的滤波器
g
θ
=
diag
(
θ
)
g_{\\theta}=\\operatorname{diag}(\\theta)
gθ=diag(θ)的乘积:
g θ ⋆ x = U g θ U ⊤ x (3) g_{\\theta} \\star x=U g_{\\theta} U^{\\top} x\\tag{3} gθ⋆x=UgθU⊤x(3)
其中 U U U是标准化图拉普拉斯的特征向量, Λ \\Lambda Λ是其特征值, U ⊤ x U^{\\top} x U⊤x是信号x的图傅里叶变换。 - 标准化的图拉普拉斯的定义为: L = I N − D − 1 2 A D − 1 2 = U Λ U ⊤ L=I_{N}-D^{-\\frac{1}{2}} A D^{-\\frac{1}{2}}=U \\Lambda U^{\\top} L=IN−D−21AD−21=UΛU⊤,那 g θ g_{\\theta} gθ就可以理解为L特征值的函数 g θ ( Λ ) g_{\\theta}(\\Lambda) gθ(Λ)。
- 但是式3的计算时间复杂度确实很高,所以本文引用了一个近似方法-切比雪夫多项式截断:
g θ ′ ( Λ ) ≈ ∑ k = 0 K θ k ′ T k ( Λ ~ ) (4) g_{\\theta^{\\prime}}(\\Lambda) \\approx \\sum_{k=0}^{K} \\theta_{k}^{\\prime} T_{k}(\\tilde{\\Lambda})\\tag{4} gθ′(Λ)≈k=0∑Kθk′Tk(Λ~)(4)
其中 Λ ~ = 2 λ max Λ − I N \\tilde{\\Lambda}=\\frac{2}{\\lambda_{\\max }} \\Lambda-I_{N} Λ~=λmax2Λ−IN,而切比雪夫多项式被定义为一种递归式: T k ( x ) = 2 x T k − 1 ( x ) − T k − 2 ( x ) T_{k}(x)=2 x T_{k-1}(x)-T_{k-2}(x) Tk(x)=2xT文献阅读19期:SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS