文献阅读04期：神经网络解释 - GRACE

Posted 2021-06-18 RaZLeon

[ 文献阅读·DL ] Outline：GRACE: Generating Concise and Informative Contrastive Sample to Explain Neural Network Model’s Prediction

推荐理由：虽然神经网络近年来越来越为人所熟知，但是网络的可解释性一直是一个值得关注的话题，而且想要这个领域作出一定成果，属实一项挑战。该论文借鉴了因果关系中的“干预解释”和哲学中的“解释性是对比性”，从而提出了一种名为GRACE的新颖解决方案，该解决方案可以更好地解释神经网络模型对表格数据集

文献全名：GRACE: Generating Concise and Informative Contrastive Sample to Explain Neural Network Model’s Prediction

1.摘要&简介

• 本文针对“表格型”数据的训练展开可解释性研究。
• 本文方法在预解释决策上，比Lime有高出60%的精度。
• 具体实施方法为：假定有两个分类标签X和Y，在一个样本给定标签为X的情况下，GRACE会产生一个被标记为Y的“负面教材”，并以此来解释原来的样本为什么会被标记为X。
• 实验涉及其他评价指标：fidelity, conciseness, info-gain, influence。
• 本文所建立的表格数据网络训练解释方法，基本面向机器学习的商业用户，也就是普通用户，不像是先前的解释算法，大多面向研究学者。
• 本文面临挑战1：表格数据经常有较高维度且相互关联的属性。因此选取top-k个特性可以减少信息冗余，让客户在看解释的时候不会太过困惑。
• 本文面临挑战2：如果是仅仅提供挑战1中所选取的几个特征，普通用户还是会被这些特征困惑到，所以本文决定将这些特征写成一些更容易理解的文本，这样客户在预测的时候能够更加准确。
• 本文面临挑战3：一般没有机器学习背景的用户对于所谓“近似决策边缘”提供的这些解释不是能够很好地理解。为此，本文加入一些对比解释，例如：“被分类为正常邮件”，会被修改为“这更像是一封正常邮件，而不是垃圾邮件。”
• 总的来说，这些挑战基本来自于普通用户对一些专业术语的不解，最终导致的错误选择。（博文笔者也认为，这种后期加工导致的精准度下降，确实十分可惜。）
• 原文所述作出的贡献为以下三点：
  

2.解释模型（THE EXPLANATION MODEL）

2.1.对比解释

• 让计算机学会去回答“为什么？”是一个非常关键的问题。比如：为什么这个病人会被诊断为这个病症，为什么这家公司会面临破产，为什么这个样本是这个物种……（“是什么”很好回答，但“为什么是这样的？”你直接这么问电脑，估计电脑会戴上痛苦面具，啊不，是你会戴上。）
• 这时候，因果关系就非常重要，用作者的话来说，这个因果概念应该是取自于哲学的因果律。
• 针对因果，论文中有这样两条描述：
  1. 如果一个结果是某个事件所导致的，那这个事件是就是起因。
  2. 然而，因果关系只能在受控制的环境下建立：在此环境中，当你改变一个输入，其他输入不变，观察输出的变化。
• 将数据科学或是机器学习代入因果律是一件不小的挑战，毕竟如果只有数据，那便很难获知因果关系。

2.2.干预解释

• 定义1：如果特征子集里的$\mathcal{P}$是预测输出$X$的解释条件，那在改变$\mathcal{P}$的时候，输出结果也将改为不同于$X$的其他分类，并且是在其他特征没有发生改变的情况下。
• 定义2：影响程度评分：
  $${\mathrm{infl}}_{\lambda }(\mathcal{P})=\frac{1(\mathrm{Y}\ne \mathrm{X})}{(\text{ Number of features in }\mathcal{P}{)}^{\lambda }}\text{\hspace{1em}(1)}$$
  其中，$1(\cdot )$是一个指示器，$X$和$Y$是干预前后的预测结果。另外，$\lambda >0$较为合理，因为这样可以让特征维持在一个比较小的数量级（特征一多，影响程度评分为1.0，这一箩筐肯定都有效，天知道哪个因子有用，对不对？）

2.3.从干预到生成

• 简单来说，就是用户很疑惑，你给我测了血压，我现在血压这个数值，究竟好还是不好？医生拿出一个健康人的血压数值告诉你，你这不好。（具体请看原文，这里太懒，就放一段自己的理解好了。）

3.目标函数

• 令$f(\cdot )$是我们想要给出实例解释的网络模型
• 定义3-对比样本（Contrastive Sample）：给定任意的样本$\mathbf{x}\in \mathcal{X}$，以及网络模型$f(\cdot )$，当$\tilde{\mathbf{x}}$满足以下条件的时候，它才能称作$\mathbf{x}$的对比样本：
  $$\underset{\tilde{\mathbf{x}}}{\min }\mathrm{dist}(\mathbf{x},\tilde{\mathbf{x}})\text{ s.t. }\mathrm{argmax}(f(\mathbf{x}))\ne \mathrm{argmax}(f(\tilde{\mathbf{x}}))\text{\hspace{1em}(2)}$$
• 而这个对比样本$\tilde{\mathbf{x}}$是用来解释$\mathbf{x}$用的。
• 需要注意的是，生成的样本$\tilde{\mathbf{x}}$还不能变得太离谱，如果你所有特征都变了，用户也没办法知道你哪个值起了作用，更别说解释起了什么作用。
• 所以，论文笔者认为，一个好的“反面教材”，应该只改掉某个或较少的几个特征，然后就能体现出变化，并且能体现这种变化的差距有多大，还不能动别的特征。
• 鉴于这样的严格要求，论文作者加入了限制3和4：
  $$|\mathcal{S}|\le K\text{\hspace{1em}(3)}$$
• $\mathcal{S}$是样本$\mathbf{x}$提取出来制作$\tilde{\mathbf{x}}$用的，比如以下这种改变：
  $$|\mathcal{S}|=\sum _{m=1}^{M}1\left({\mathrm{x}}^{\mathrm{m}}\ne {\tilde{\mathrm{x}}}^{\mathrm{m}}\right)\text{\hspace{1em}(4)}$$
• 当然，有上面这个要求还不够，你特征的限制是小起来了，但你这个数值的变化得够明显，（变个0.1用户还是看不出来啊）那就加限制条件！：
  $$\mathrm{SU}\left(X^i,X^j\right)\le \gamma \forall i,j\in \mathcal{S}\text{\hspace{1em}(5)}$$
• $\gamma$就是对称不确定性函数$\mathrm{S}\mathrm{U}(\cdot )$的上界，一个正则化的共享信息，4.2会介绍。
• 最后为了确保特征$\mathcal{P}$贴近真实，我们还得加限制（比如说，年龄总得是个正数，对吧）：
  $$\tilde{\mathbf{x}}\in \mathrm{dom}(\mathcal{X})\text{\hspace{1em}(6)}$$
• 集齐上面五颗龙珠，可以召唤神龙，目标函数了：
  

4.格蕾丝本体（GRACE）

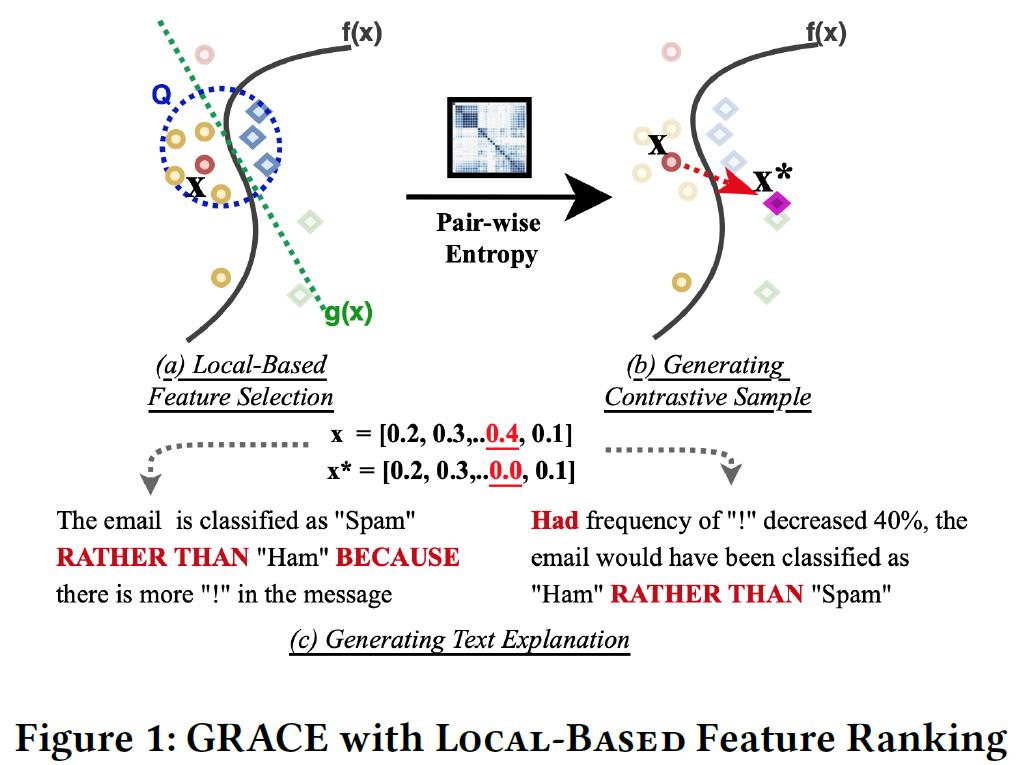
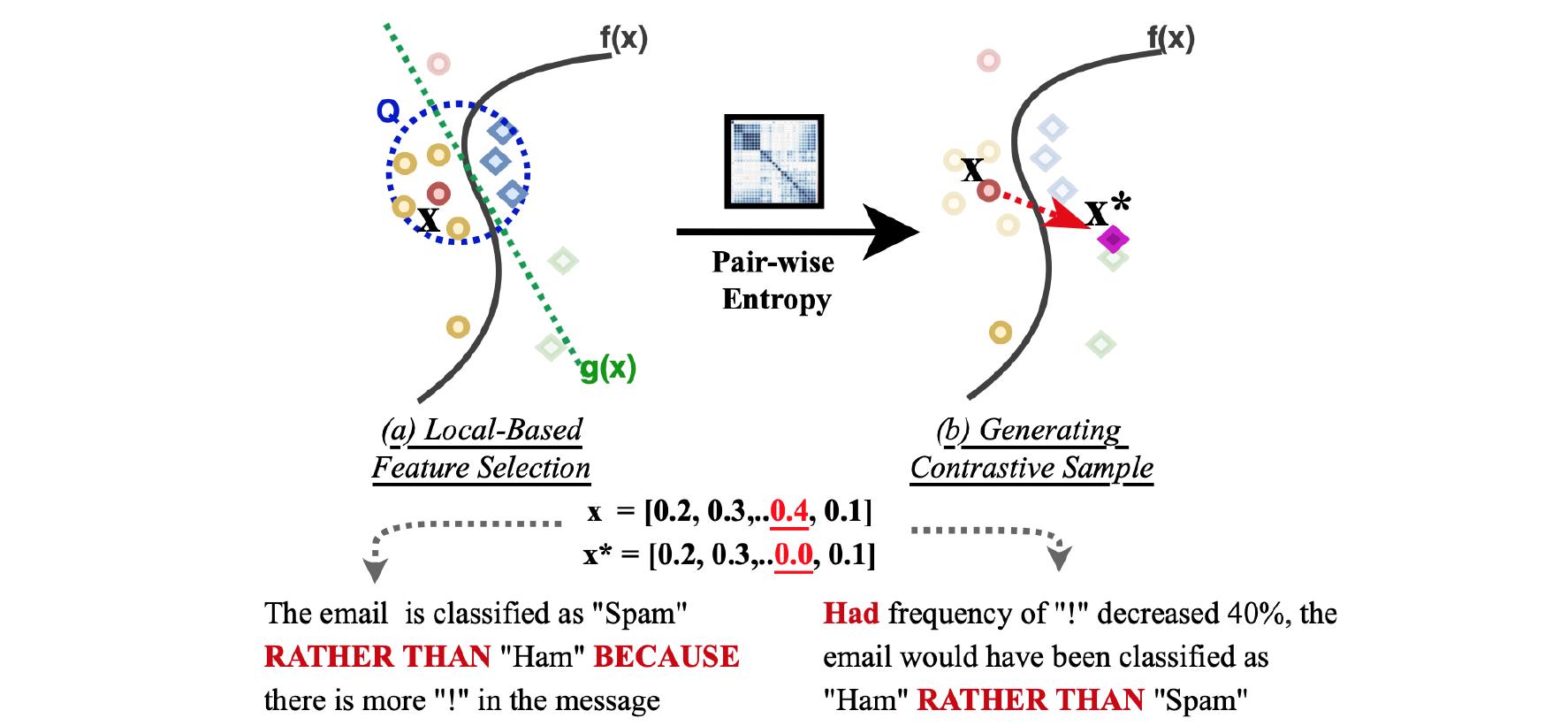
• 如图，核心 · 格蕾丝（GRACE）计划分为三个步骤：

1. 根据信息熵理论，找出一个排序，用于排列基于实例的特征，并且这些特征满足限制条件；
2. 根据这些排列过的特征，找几个影响还不错的，来做出用于解释原实例的“反面教材”；
3. 基于产生的“反面教材”，产生解释文本。

• 算法描述如下：
  

4.1.对比样本生成算法

• 论文依据下式构建正交投影向量，用于描述“反面教材”$\tilde{\mathbf{x}}$：
  r v = ∣ f v ( x ~ i − 1 ) − f C ( x ) ∣ ∥ ∇ f v ( x ~ i − 1 ) − ∇ f C ( x ) ∥ 2 2 ( ∇ f v ( x ~ i − 1 ) − ∇ f C ( x ) ) (8) \\mathbf{r}_{v}=\\frac{\\left|f_{v}\\left(\\tilde{\\boldsymbol{x}}_{i-1}\\right)-f_{C}(\\boldsymbol{x})\\right|}{\\left\\|\\nabla f_{v}\\left(\\tilde{\\boldsymbol{x}}_{i-1}\\right)-\\nabla f_{C}(\\boldsymbol{x})\\right\\|_{2}^{2}}\\left(\\nabla f_{v}\\left(\\tilde{\\boldsymbol{x}}_{i-1}\\right)-\\nabla f_{C}(\\boldsymbol{x})\\right)\\tag{8} rv​=∥∇fv​(x~i−1​)−∇fC​(x)∥22​∣fv​(x~i−1​)−fC​(x)∣​(∇fv​(x~i−1​)−∇fC​(x))<

  以上是关于文献阅读04期：神经网络解释 - GRACE的主要内容，如果未能解决你的问题，请参考以下文章

  文献阅读17期：Deep Learning on Graphs: A Survey - 6

  文献阅读16期：Deep Learning on Graphs: A Survey - 5

  文献阅读12期：Deep Learning on Graphs: A Survey - 1

  文献阅读17期：Deep Learning on Graphs: A Survey - 6

  文献阅读15期：Deep Learning on Graphs: A Survey - 4

  文献阅读14期：Deep Learning on Graphs: A Survey - 3