文献阅读06期：基于Logistic效用函数智能电网定价

Posted RaZLeon

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了文献阅读06期：基于Logistic效用函数智能电网定价相关的知识，希望对你有一定的参考价值。

[ 文献阅读·能源 ] The real-time pricing optimization model of smart grid based on the utility function of the logistic function [1]

推荐理由：需求侧响应（需求侧管理）与社会福利最大化最近几年在能源领域逐渐受到重视，本文提出一种基于Logistic效用函数

1.摘要&简介

  • 效用函数是求解智能电网实时电价的一个非常关键的因素。本文根据Logistic函数提出一种新型效用函数。
  • 问题构建完成之后，本文通过KKT条件和Fischer-Burmerister光滑函数求解。
  • 将非光滑函数转换为光滑函数后，采用光滑牛顿法求解问题。

2.系统模型

  • 本文研究环境为单电力供应商外加一种用户。

2.1.Logistic效用函数

  • 本文提出Logistic效用函数为：
    U ( x n h , ω n h ) = K ~ ( e ω n h x n h − 1 ) e ω n h λ n h + 1 (5) U\\left(x_n^h, \\omega_n^h\\right)=\\frac\\tildeK\\left(e^\\omega_n^h x_n^h-1\\right)e^\\omega_n^h \\lambda_n^h+1\\tag5 U(xnh​,ωnh​)=eωnh​λnh​+1K~(eωnh​xnh​−1)​(5)
  • 此函数用图标绘制出为下图形式：

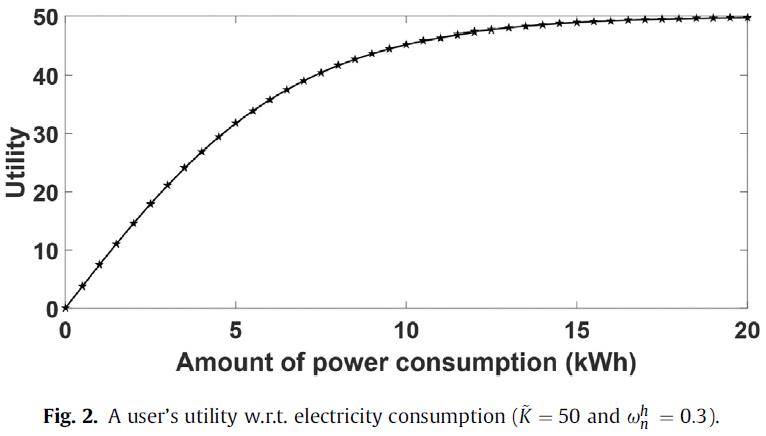
2.2.用户福利函数

  • 社会福利函数：
    B u = ∑ n ∈ N U ( x n h , ω n h ) − p h ∑ n ∈ N x n h (6) B_u=\\sum_n \\in \\mathscrN U\\left(x_n^h, \\omega_n^h\\right)-p^h \\sum_n \\in \\mathscrN x_n^h\\tag6 Bu​=n∈N∑​U(xnh​,ωnh​)−phn∈N∑​xnh​(6)
    其中，前半部分为效用函数，后半部分代表所付电费。
  • 则福利函数对 x n h x_n^h xnh​求导则有：
    ∂ B u ∂ x n h = 2 K ~ ω n h e ω n h x n h ( e ω n h x n h + 1 ) 2 − p h (7) \\frac\\partial B_u\\partial x_n^h=\\frac2 \\tildeK \\omega_n^h e^\\omega_n^h x_n^h\\left(e^\\omega_n^h x_n^h+1\\right)^2-p^h\\tag7 ∂xnh​∂Bu​​=(eωnh​xnh​+1)22K~ωnh​eωnh​xnh​​−ph(7)
    令 ∂ B u ∂ x n h = 0 \\frac\\partial B_u\\partial x_n^h=0 ∂xnh​∂Bu​​=0，易得： p h = 2 K ~ ω n h e ω n h x n h ( e ω n n h x n h + 1 ) 2 ( = V ( x n h , ω n h ) ) p^h=\\frac2 \\tildeK \\omega_n^h e^\\omega_n^h x_n^h\\left(e^\\omega n_n^h x_n^h+1\\right)^2\\left(=V\\left(x_n^h, \\omega_n^h\\right)\\right) ph=(eωnnh​xnh​+1)22K~ωnh​eωnh​xnh​​(=V(xnh​,ωnh​))
  • 由此易得 p h p^h ph图像如下：

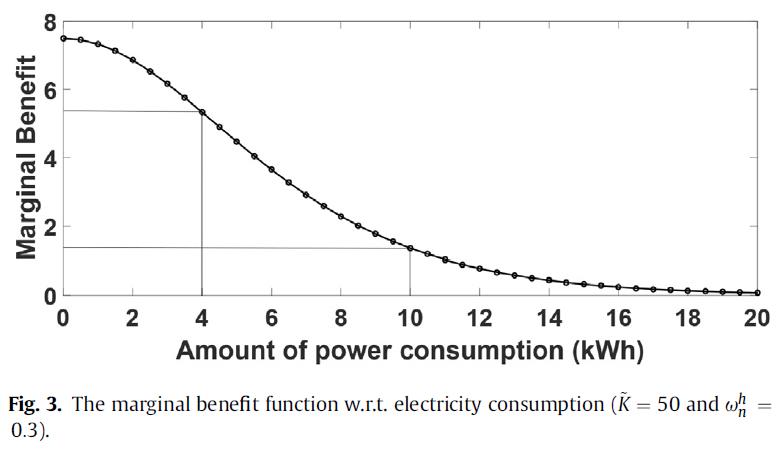
2.3.供电商利润