机器学习 Machine Learning- 吴恩达Andrew Ng 第16~20课总结

Posted 2021-06-12 架构师易筋

YouTube课程地址

https://www.youtube.com/playlist?list=PLOXON7BTL9IW7Ggbc09jLqGmzkwPI4-3V
截止2021-5-3, 有112 个视频

1. 第16课 Matrix-matrix multiplication， Linear regression with one variable

矩阵相乘，可以等价于左边矩阵逐个乘以右边矩阵的列向量。

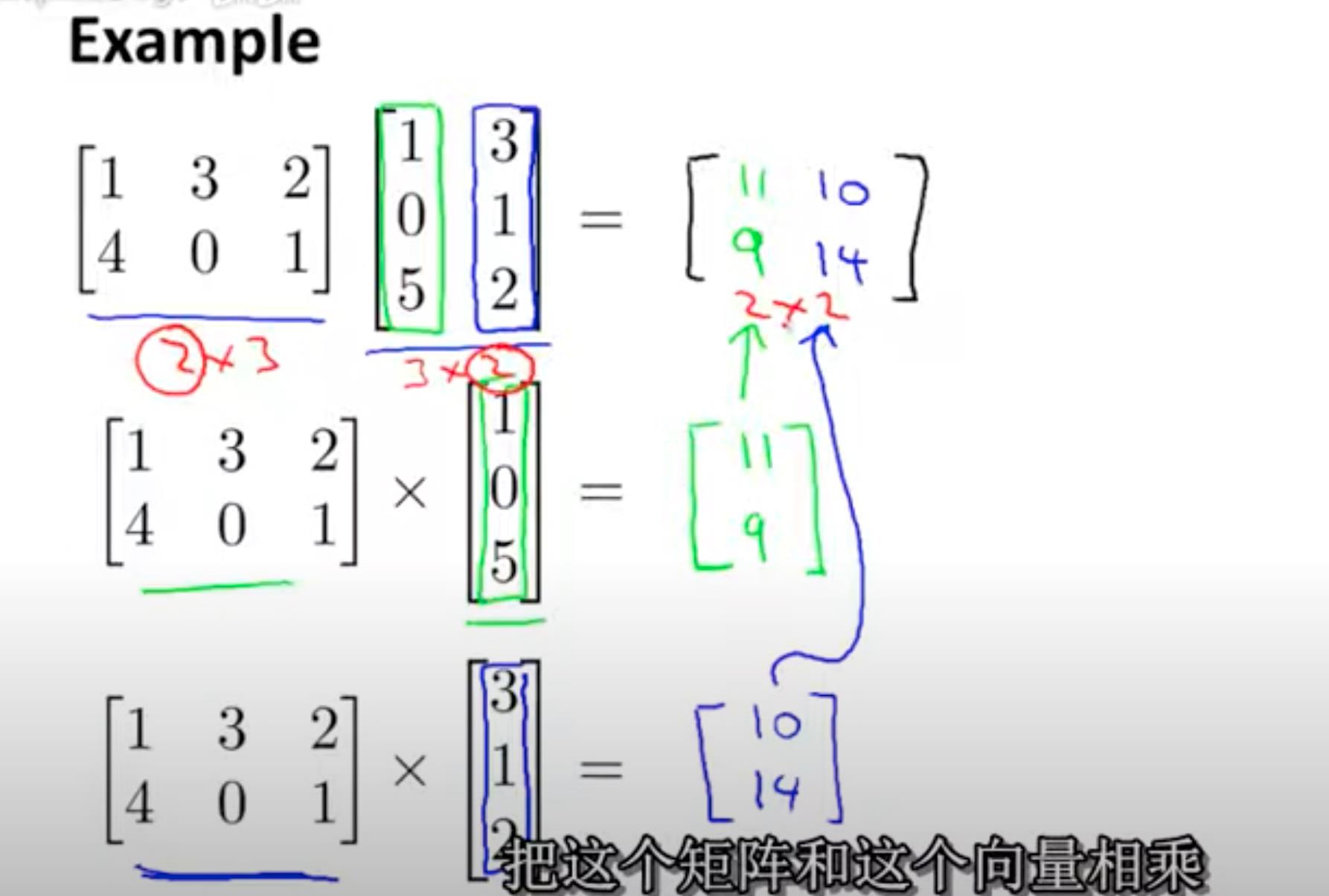
矩阵相乘公式演示：矩阵相乘，可以等价于左边矩阵逐个乘以右边矩阵的列向量。

矩阵相乘的应用例子：比如根据房子大小预测房价，有三个预测公式，可以一次得到3个结果。

2. 第17课 Matrix multiplication properties， Linear regression with one variable

矩阵乘法正常情况下，不支持乘法交换律

矩阵支持相邻的乘法结合律，A * B * C = A * (B * C ) = (A * B) * C

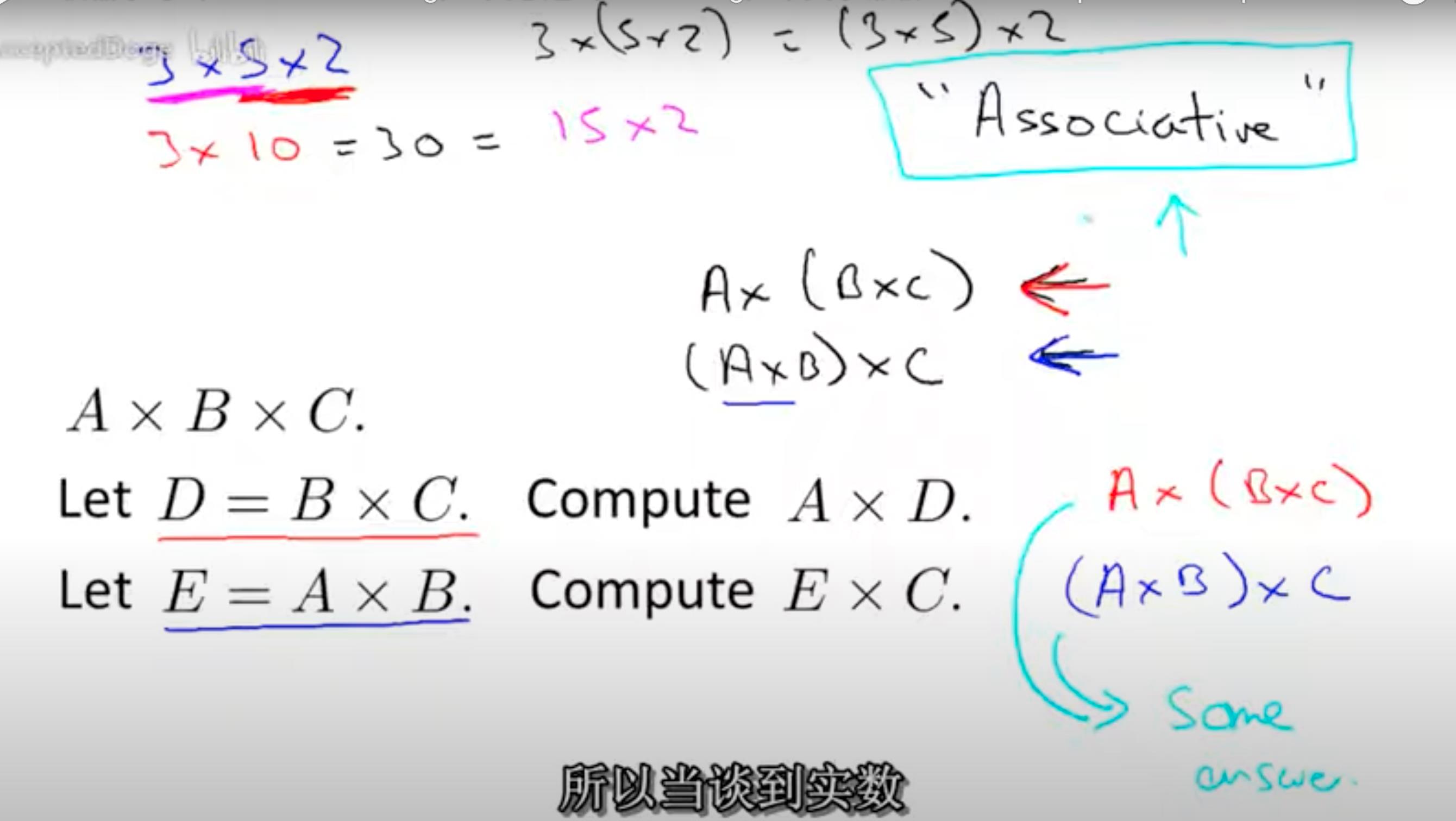
• 乘法交换律与标量相乘的情况下，成立。但是左边的标量矩阵，和右边的标量的[n, n]数,[m, m]数 不一定相等。
• 标量矩阵表示左上角到右下角的对角线上是1， 其它位置都是0.

3. 第18课 Inverse and transpose逆矩阵和转置矩阵 - Linear regression with one variable

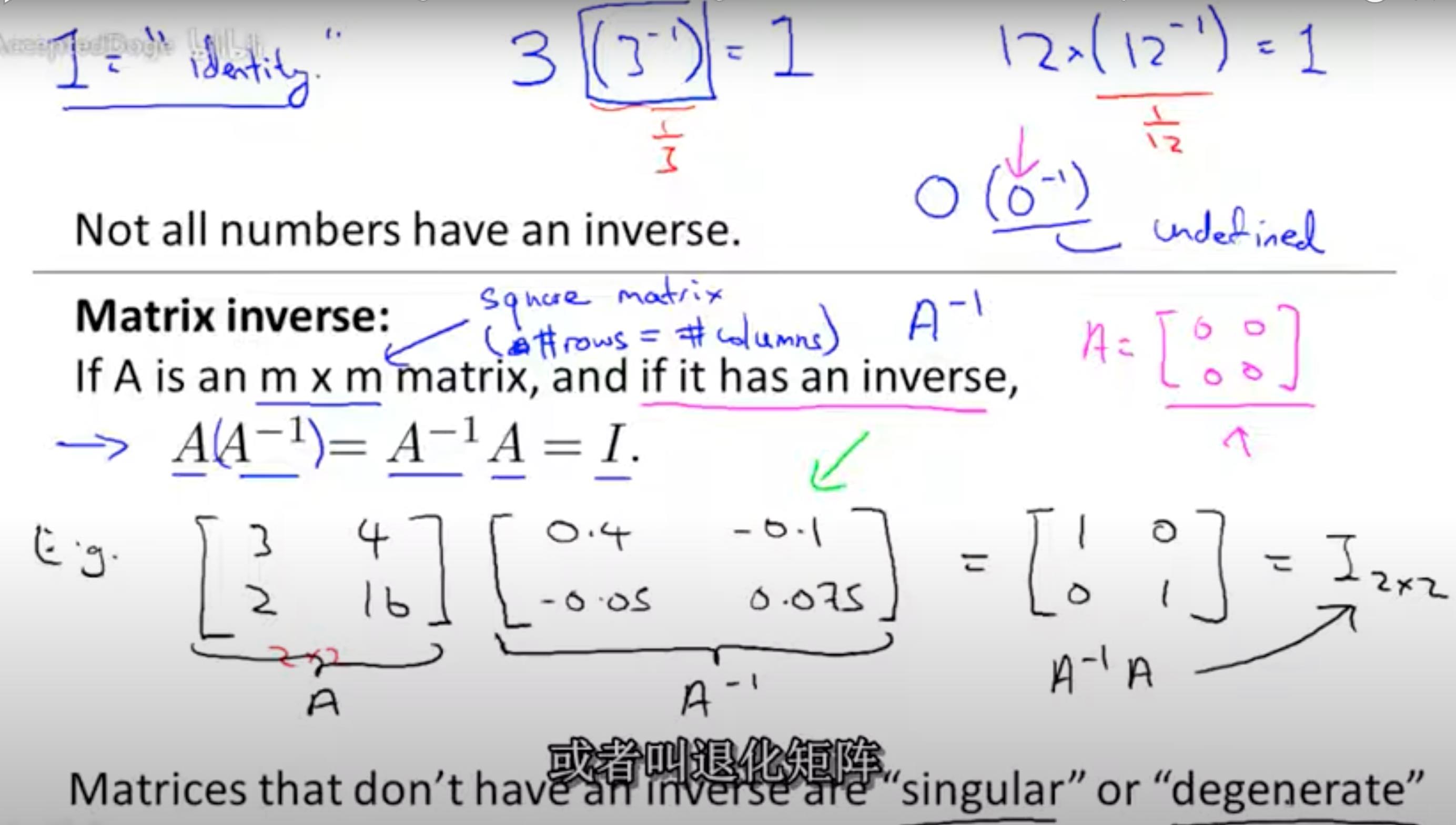
• 逆矩阵表示，A * (A -1) = I 矩阵和矩阵的逆矩阵相乘等于标量矩阵。
• 注意：不是所有矩阵都有逆矩阵，比如[0]矩阵。
• 没有逆矩阵的矩阵叫做Singular 奇异矩阵 或者 Degenerate 退化矩阵
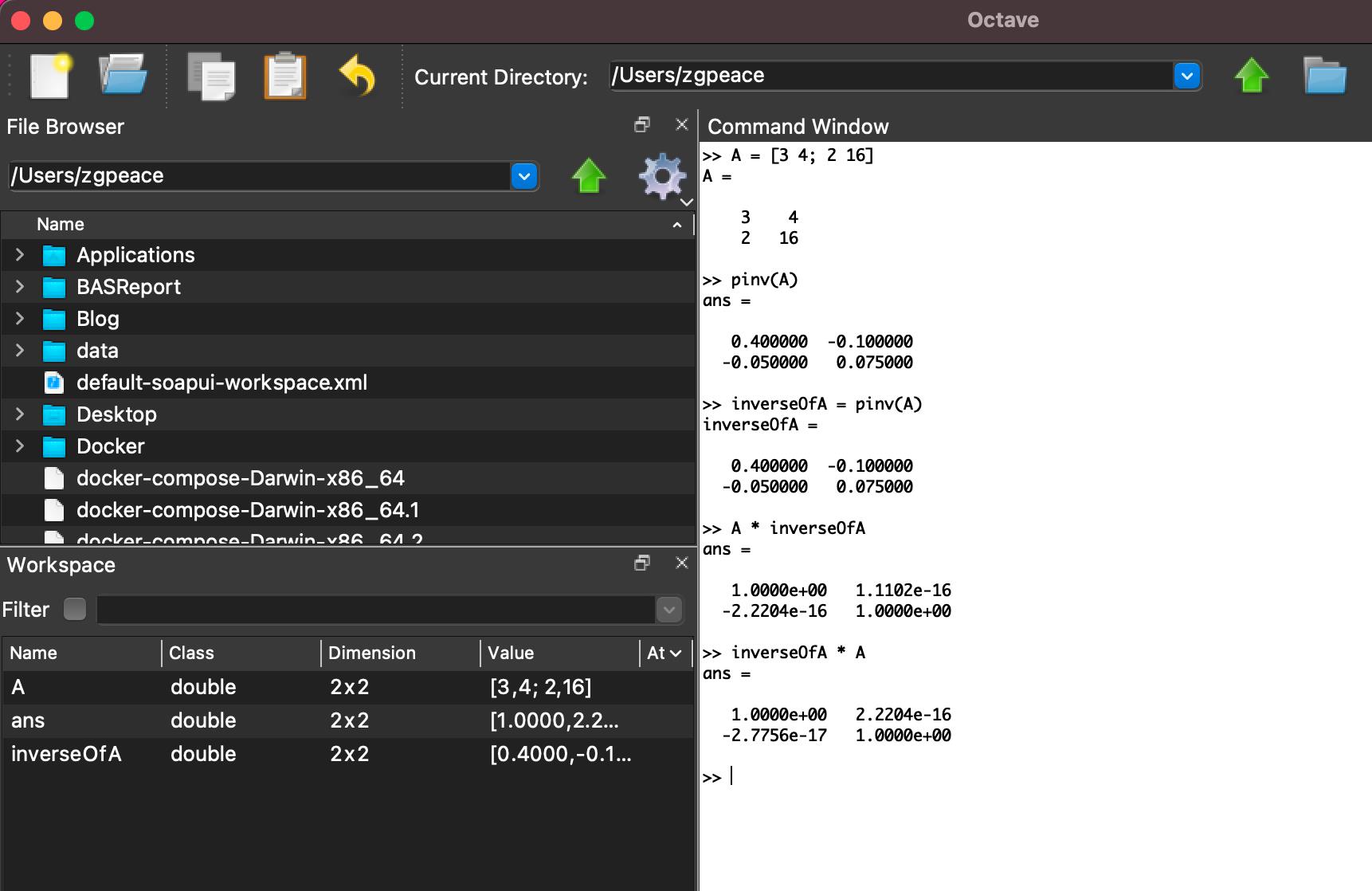
  用Octave 计算逆矩阵的过程如下：
  由于精度问题 0 ≈ 1.1102e-16 ， 0 ≈ -2.2204e-16

>> A = [3 4; 2 16]
A =

    3    4
    2   16

>> pinv(A)
ans =

   0.400000  -0.100000
  -0.050000   0.075000

>> inverseOfA = pinv(A)
inverseOfA =

   0.400000  -0.100000
  -0.050000   0.075000

>> A * inverseOfA
ans =

   1.0000e+00   1.1102e-16
  -2.2204e-16   1.0000e+00

>> inverseOfA * A
ans =

   1.0000e+00   2.2204e-16
  -2.7756e-17   1.0000e+00

>>

转置矩阵，表示行和列互换的矩阵。特性为 Bij = Aji.

4. 第19课 Multiple features 更多参数 - Linear regression with one variable

回顾：根据房子大小，预测房价的公式如下

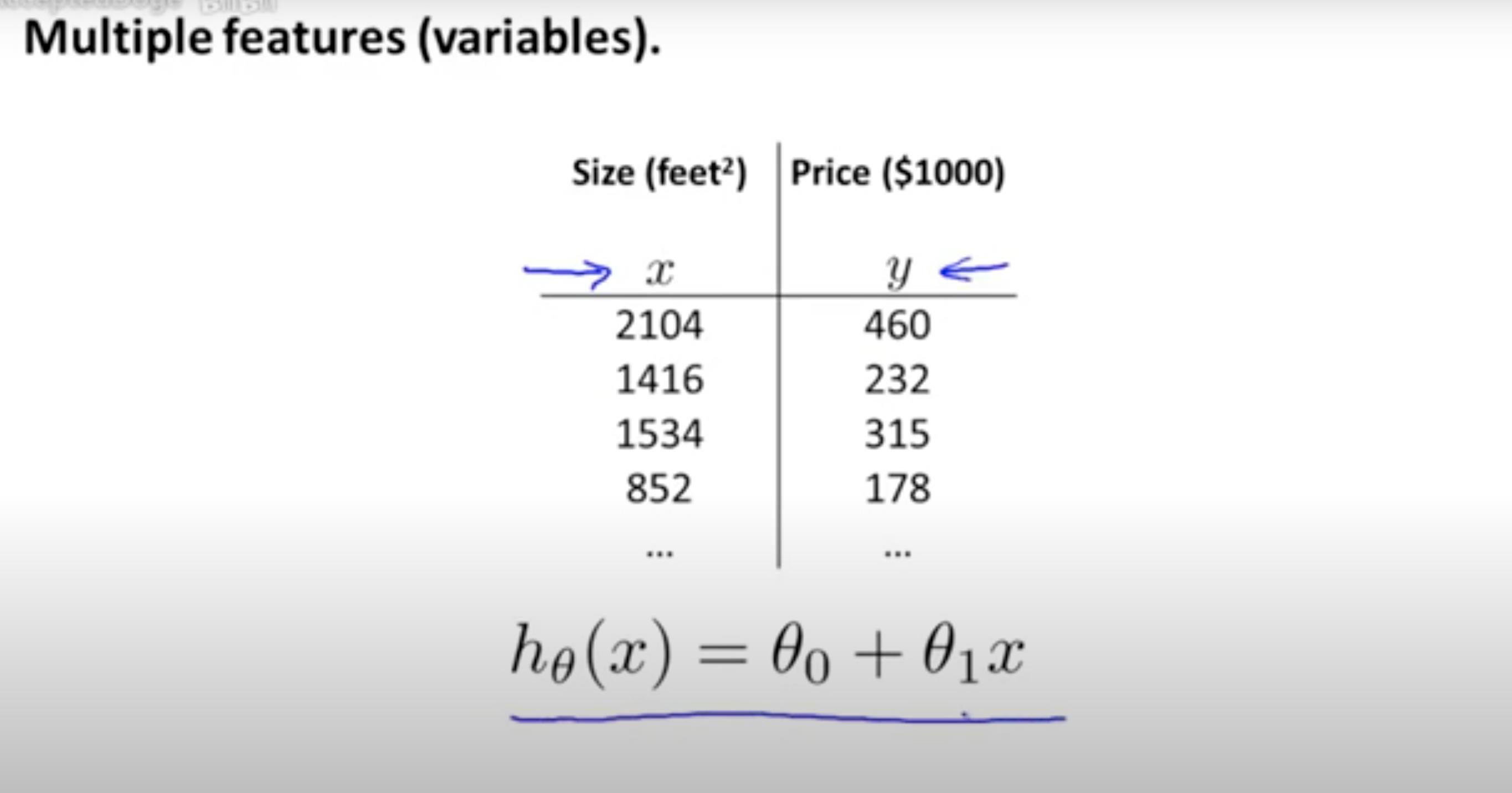
比较有现实意义，根据房子大小，房子的个数，房子楼层数，房子楼龄，预测房子价格。

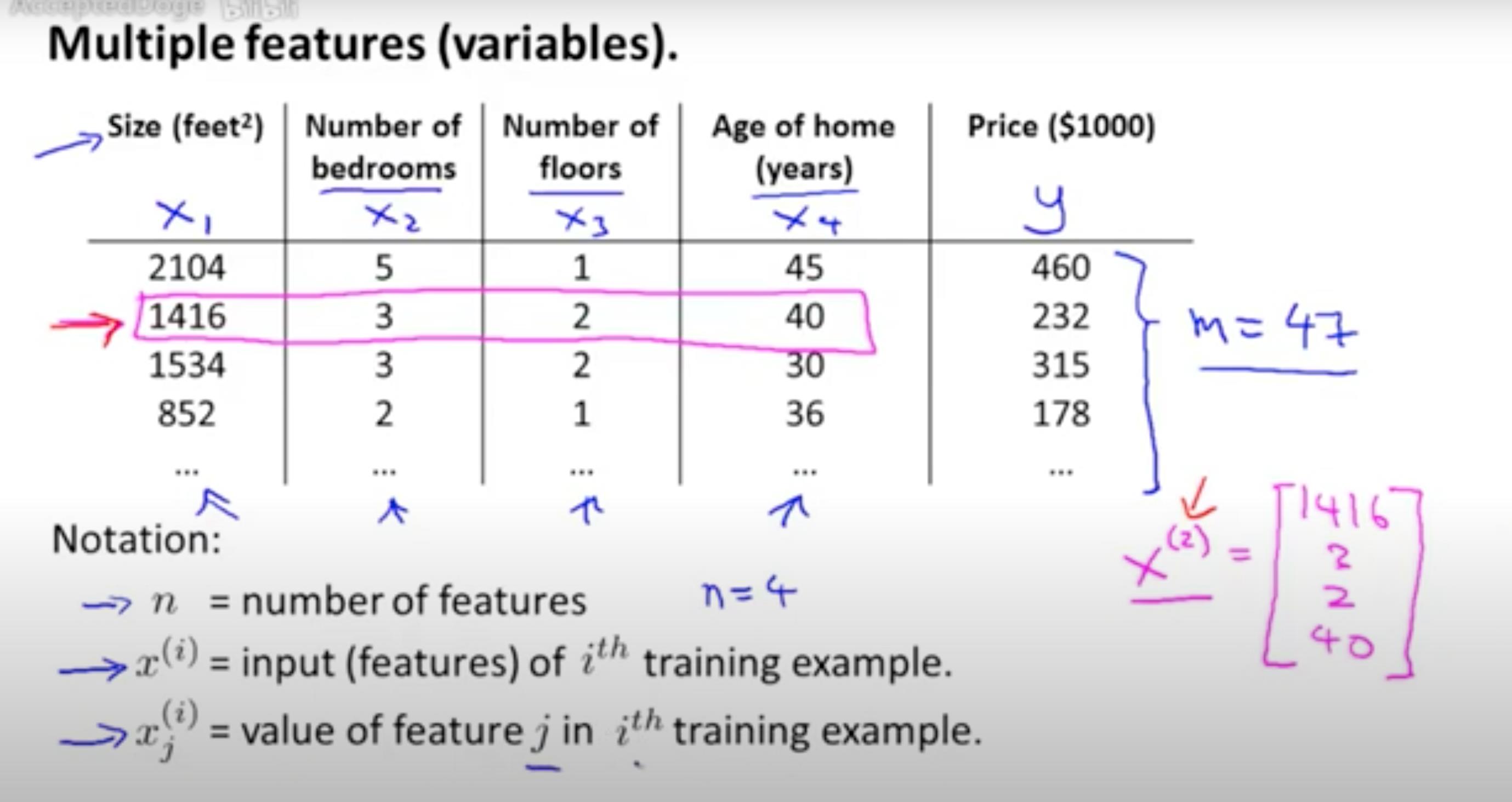
根据房子大小，房子的个数，房子楼层数，房子楼龄，预测房子价格。4个参数的公式如下：

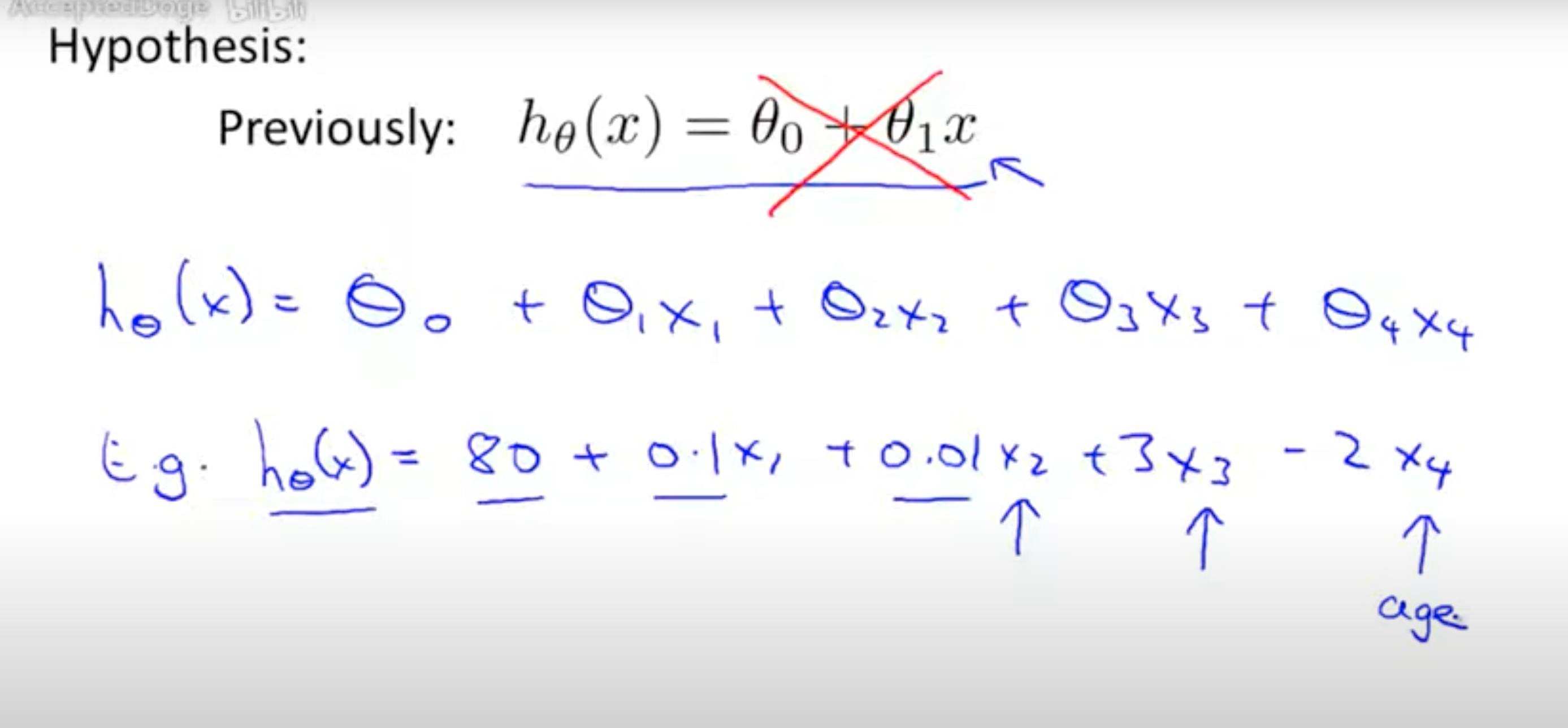
多个参数通用的推导公式如下：

4. 第20课 Gradient descent for multiple variables 梯度下降用多元方程求解 - Linear regression with one variable

假设方程，耗能方程，梯度下降方程如下。（这里不是很理解，要多看看？？）

梯度下降方程的系数求解如下：（不是很理解，要多看看？？）