线性代数
Posted zizi7
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性代数相关的知识,希望对你有一定的参考价值。
目录
A x = b Ax=b Ax=b无解时的求解
从线性代数(1)列空间的讨论可知,如果 b b b不在 A A A的列空间 C ( A ) C(A) C(A)内,那么 A x = b Ax=b Ax=b无解
在实际应用中这种无解的情况很多:
1)因为观察/测量的数据总会有误差,无法保证每个
b
i
b_i
bi都是精确的;
2)未知数少,而限制条件多
先说结论:将
A
x
=
b
Ax=b
Ax=b转为求
A
T
A
x
^
=
A
T
b
(1)
A^TA\\hatx=A^Tb \\tag1
ATAx^=ATb(1)
- 式(1)的解是 A x = b Ax=b Ax=b的最优解
- 如果 C ( A ) C(A) C(A)线性无关,那么 A T A A^TA ATA必然可逆
空间投影
先探讨一维向量空间的情况
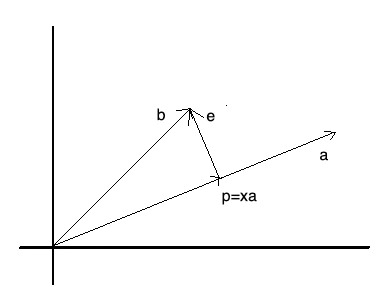
如图1,
p
⃗
\\vecp
p是
b
⃗
\\vecb
b在
a
⃗
\\veca
a上的投影,有
p
⃗
=
x
a
⃗
e
⃗
=
b
⃗
−
p
⃗
(2)
\\vecp=x\\veca\\\\\\vece=\\vecb-\\vecp \\tag2
p=xae=b−p(2)
显然,
e
⃗
\\vece
e垂直于
a
⃗
\\veca
a,根据正交向量点积为0的定理,有
a
T
(
b
−
x
a
)
=
0
⇒
x
=
a
T
b
a
T
a
⇒
p
=
x
a
=
a
a
T
b
a
T
a
⇒
P
=
a
a
T
a
T
a
(3)
a^T(b-xa)=0\\\\\\Rightarrow x=\\fraca^Tba^Ta\\\\\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\Rightarrow p=xa=a\\fraca^Tba^Ta\\\\\\Rightarrow P=\\fracaa^Ta^Ta \\tag3
aT(b−xa)=0⇒x=aTaaTb ⇒p=xa=aaTaaTb⇒P=aTaaaT(3)
式(3)中
P
P
P为投影矩阵,将
b
⃗
\\vecb
b投影到
a
⃗
\\veca
a上
投影矩阵3条性质:
1.秩为1(如式3,投影矩阵为列向量与行向量乘积,满足秩1矩阵的性质)
2.转置不变: P T = P P^T=P PT=P,说明投影矩阵是对称矩阵
3.平方不变: P 2 = P P^2=P P2=P(投影2次和投影1次结果一样)
现在在二维空间中讨论
A
x
=
b
Ax=b
Ax=b解的问题
假设
A
A
A的列空间基为
a
1
a_1
a1、
a
2
a_2
a2,那么当
b
b
b不在
a
1
a_1
a1和
a
2
a_2
a2确定的平面内时,
A
x
=
b
Ax=b
Ax=b无解
现在假设
c
c
c是
b
b
b在
a
1
a_1
a1和
a
2
a_2
a2确定的平面上的投影,即
c
=
x
^
1
a
1
+
x
^
2
a
2
(4)
c=\\hatx_1a_1+\\hatx_2a_2 \\tag4
c=x^1a1+x^2a2(4)
那么
A
x
^
=
c
A\\hatx=c
Ax^=c肯定有解,而且是
A
x
=
b
Ax=b
Ax=b误差最小的解
令 e e e为从 b b b到 c c 以上是关于线性代数的主要内容,如果未能解决你的问题,请参考以下文章
机器学习|数学基础Mathematics for Machine Learning系列之线性代数(16):方阵的特征值与特征向量