自动驾驶车辆运动学模型
Posted CHH3213
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了自动驾驶车辆运动学模型相关的知识,希望对你有一定的参考价值。
文章目录
参考资料
模型的用处就是在当前状态给定某控制输入时,预测(估计) 系统未来的状态。控制领域利用模型设计合适的输入,以期控制系统到达目标状态。
1. 以车辆重心为中心的单车运动学模型
1.1 参数说明
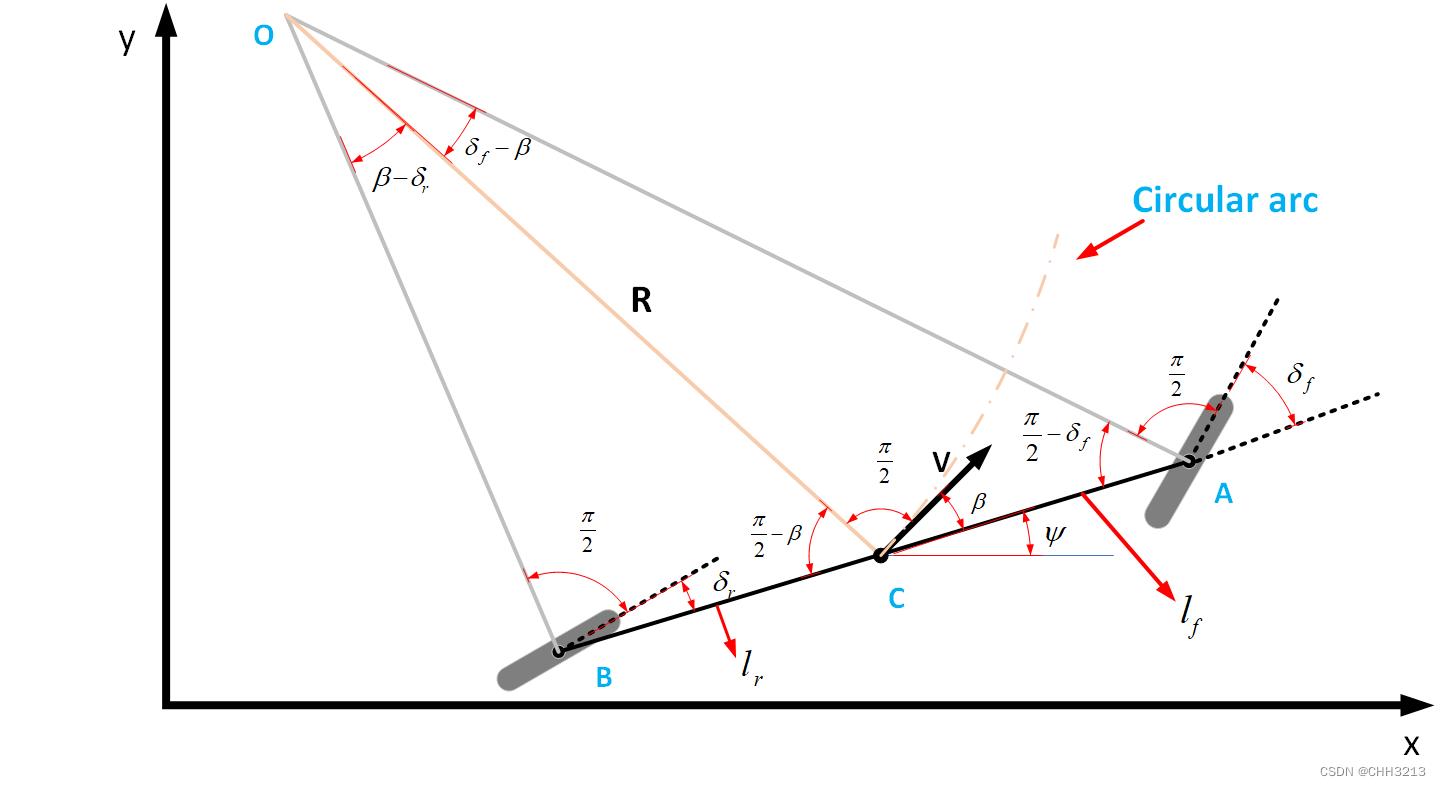
一般考虑运动学模型时,将车辆模型简化成单车模型(bicycle model)。
单车模型中:
-
左右轮等效为单个轮子
左右前轮合并为单个轮子,其中心点为A点,同样后轮等效后的中心点为 B点。 -
转向角
前后轮的转向角用 δ f \\delta_f δf和 δ r \\delta_r δr表示,模型中前后轮都可以转向,对于只有前轮转向的系统,后轮转向角 δ r \\delta_r δr可以设置为0. -
重心
点 C 代表车辆的重心, A 点和 B点到重心的距离分别用 l f l_f lf和 l r l_r lr表示,轴距表示为 L = l f + l r L = l_f + l_r L=lf+lr。 -
速度
车辆重心的速度用 V V V表示,与车辆纵向轴的夹角为 β \\beta β,该角度叫做车辆的滑移角。 -
运动描述
假设车辆平动,车辆运动状态可以用三个坐标量描述: x x x 、 y y y 和 ψ \\psi ψ。其中 ( x , y ) (x,y) (x,y)代表车辆的位置, ψ \\psi ψ描述的是航向角(Heading Angle),指车身与X轴的夹角。 -
条件假设
假设速度矢量 V V V的方向在点 A A A点和 B B B点的方向与转向角的方向相同,换句话说,在A点的速度矢量与车辆纵轴的夹角为 δ f \\delta_f δf,同样 B B B点的速度矢量与车辆纵轴的夹角为 δ r \\delta_r δr。也就是说前后轮的滑移角 β \\beta β都为0。该条件假设成立前提的是车辆速度很低(<5m/s),此时轮胎产生的横向力很小,可以忽略。 -
轨迹半径
点 O O O代表车辆的瞬时旋转中心,线段 A O AO AO与 B O BO BO与前后两个转轮方向垂直,他们的交点即为 O O O点,线段 O C OC OC的长度代表车辆的轨迹半径 R R R。 -
航迹角
车辆重心处的速度垂直于 O C OC OC,车辆速度矢量与车辆纵轴的夹角为 β \\beta β,车辆的航向角为 ψ \\psi ψ,则航迹角为 γ = ψ + β \\gamma = \\psi + \\beta γ=ψ+β。
1.2 几何关系
1.2.1 偏航角 ψ \\psi ψ的关系
如上图所示,在三角形
O
C
A
OCA
OCA中,根据正弦定理,有:
sin
(
δ
f
−
β
)
l
f
=
sin
(
π
2
−
δ
f
)
R
(1)
\\tag1 \\frac\\sin \\left(\\delta_f-\\beta\\right)l_f=\\frac\\sin \\left(\\frac\\pi2-\\delta_f\\right)R
lfsin(δf−β)=Rsin(2π−δf)(1)
在三角形
O
B
C
OBC
OBC中,根据正弦定理,有:
sin
(
β
−
δ
r
)
l
r
=
sin
(
π
2
+
δ
r
)
R
(2)
\\tag2 \\frac\\sin \\left(\\beta-\\delta_r\\right)l_r=\\frac\\sin \\left(\\frac\\pi2+\\delta_r\\right)R
lrsin(β−δr)=Rsin(2π+δr)(2)
展开公式(1)(2)可得:
sin
δ
f
cos
β
−
sin
β
cos
δ
f
l
f
=
cos
δ
f
R
(3)
\\tag3 \\frac\\sin \\delta_f \\cos \\beta-\\sin \\beta \\cos \\delta_fl_f=\\frac\\cos \\delta_fR
lfsinδfcosβ−sinβcosδf=Rcosδf(3)
sin
β
cos
δ
r
−
cos
β
sin
δ
r
l
r
=
cos
δ
r
R
(4)
\\tag4 \\frac\\sin \\beta\\cos \\delta_r -\\cos \\beta \\sin \\delta_rl_r=\\frac\\cos \\delta_rR
lrsinβcosδr−cosβsinδr=Rcosδr(4)
等式(3)两边同时乘
l
f
cos
(
δ
f
)
\\fracl_f\\cos \\left(\\delta_f\\right)
cos(δf)lf 得
tan
(
δ
f
)
cos
(
β
)
−
sin
(
β
)
=
l
f
R
(5)
\\tag5 \\tan \\left(\\delta_f\\right) \\cos (\\beta)-\\sin (\\beta)=\\fracl_fR
tan(δf)cos(β)−sin(β)自动驾驶运动学模型的线性离散化
自动驾驶 4-2 Lesson 2: The Kinematic Bicycle Model