2021年MathorCup数学建模A题自动驾驶中的车辆调头问题全过程解题论文及程序

Posted 2022-08-22 数模竞赛Paid answer

2021年MathorCup数学建模A题自动驾驶中的车辆调头问题全过程解题标准论文及程序
  自动驾驶是近年人工智能应用的热门研究领域之一，其中调头是自动驾驶中一个非常实际又很有趣的场景。假设无人车为四轮乘用车，采用前轮转向后轮驱动；车身可认为是一个矩形，车长 5 米，车宽 2 米，轴距 2.8米；方向盘最大转角 470°，方向盘与前轮转角的传动比为 16：1（方向盘每转动 16°，前轮转动 1°），方向盘最大转速为 400°/s；最大油门加速度 3m/s`2，极限刹车加速度-5m/s^2。
  无人车的轨迹，指的是一条含有位置和时间等信息的曲线，它由一列轨迹点构成，各个轨迹点中应包含位置坐标、方向角、曲率、曲率变化率、速度、加速度及运动到此点时的时间等信息。这里轨迹指的是车身中某一特定点的轨迹，即控制点。控制点是事先选定的，通常位于无人车车身对称轴（车身可以近似认为是左右轴对称的）上的一点，在行驶时，控制点的位置会与轨迹点相重合，控制点处的速度方向将与轨迹点的方向角一致。由于无人车的车辆动力学性质和安全性要求，轨迹必须满足以下条件：
  （1）任何点的加速度不得高于最大油门加速度，不得低于极限刹车减速度；
  （2）无人车朝向和方向盘转角都不能突变，轨迹线必须是连续、且切线方向连续，当无人车不是静止时，曲率也必须连续（静止时可以原地打方向，非静止时不能）；
  （3）轨迹线的最大曲率应尽量不高于 0.205，禁止高于 0.21；
  （4）按轨迹行驶时，在调头完成之前，无人车车身任何点不得与任何障碍物或者掉头区域边界发生碰撞，且与障碍物至少保留一个最小安全距离，一般不小于 30cm。
  无人车调头轨迹在保证上述条件之外也应具备尽可能舒适的驾乘体感，以及具备尽可能高的通行效率，同时出于规范驾驶的考虑，尽量减少不必要的压车道线行驶。
  请参赛者按照下面问题中简化版的无人车调头场景和附件数据，建立无人车安全快速调头的数学模型，设计无人车调头轨迹的计算方法，在输入外部道路和障碍物信息后，计算出合理可行的无人车轨迹。同时，由于附近障碍物可能由于视野问题被遮挡，导致调头中周围环境信息发生变化，轨迹应当是可以实时更新的。附件数据文件中的边界线均表示为折线点列，按坐标点从上到下的顺序连接形成；所有障碍物均以多边形表示，其中的点均按逆时针顺序排列，路况简图见数据文件。请你们的参赛队完成以下问题：
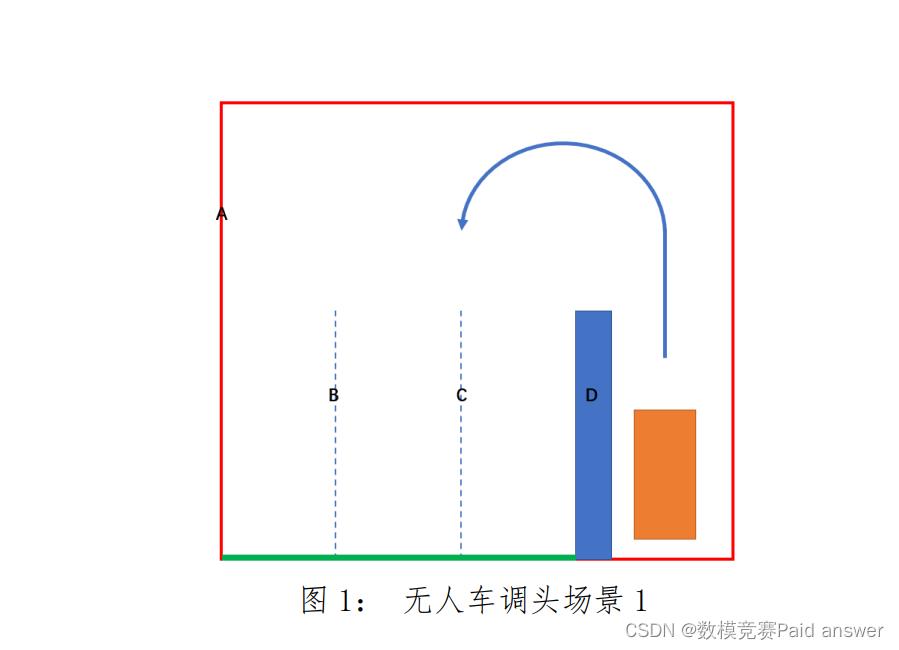
  问题 1：如图 1 所示场景，无人车（用橙色矩形表示）正在最左侧车道准备调头，存在三个对向车道。附件数据文件中，掉头区域边界以红色边框 A 表示，两条对向车道线以 B、C 表示（均为路面上的虚线），中间的隔离障碍物以 D 表示。无人车起始位置已经在附件数据文件中给出，当无人车身触碰到对向的掉头区域边界（图 1 中绿色部分）时，认为调头完成。请阐述控制点位置，解释其理由；基于此建立无人车调头的数学模型，并给出一个合理可行的算法设计，给出调头轨迹。

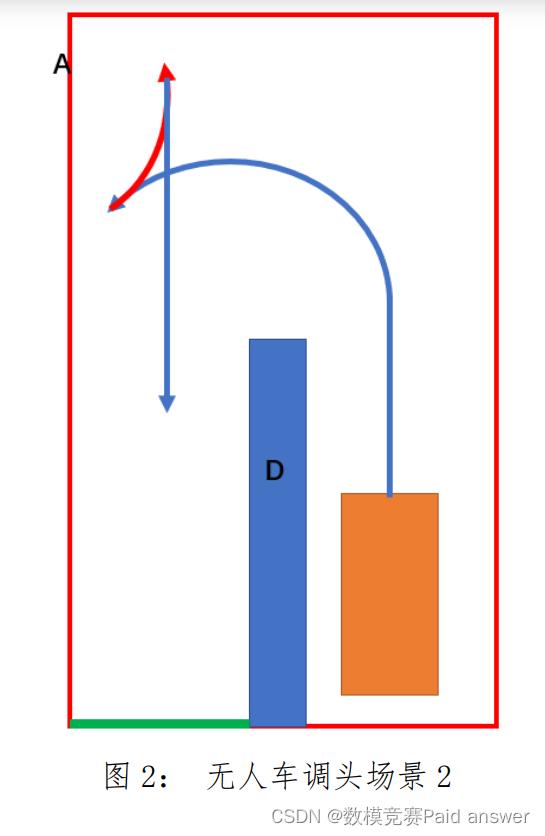
  问题 2：当掉头区域狭窄时，判断什么样的场景下无人车能够在不倒车的情况下完成调头，什么情况需要至少一次倒车（如图 2 场景 2，蓝色箭头表示向前，红色箭头表示倒车）才能通过。建立相应的无人车调头的数学模型，给出合理的算法设计，并给出仿真结果。

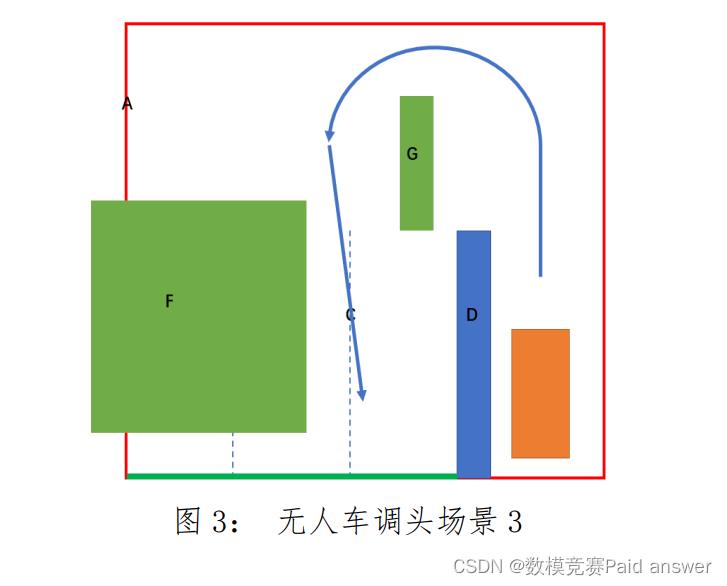
  问题 3：如图 3 场景，如果道路上还存在其它静止障碍物（附件数据文件中以 F 和 G 表示），当仅存在 F、仅存在 G、或二者都存在时，建立相应的无人车调头的数学模型，给出合理的算法设计，并给出调头轨迹，你的算法应明确如何进行避障？

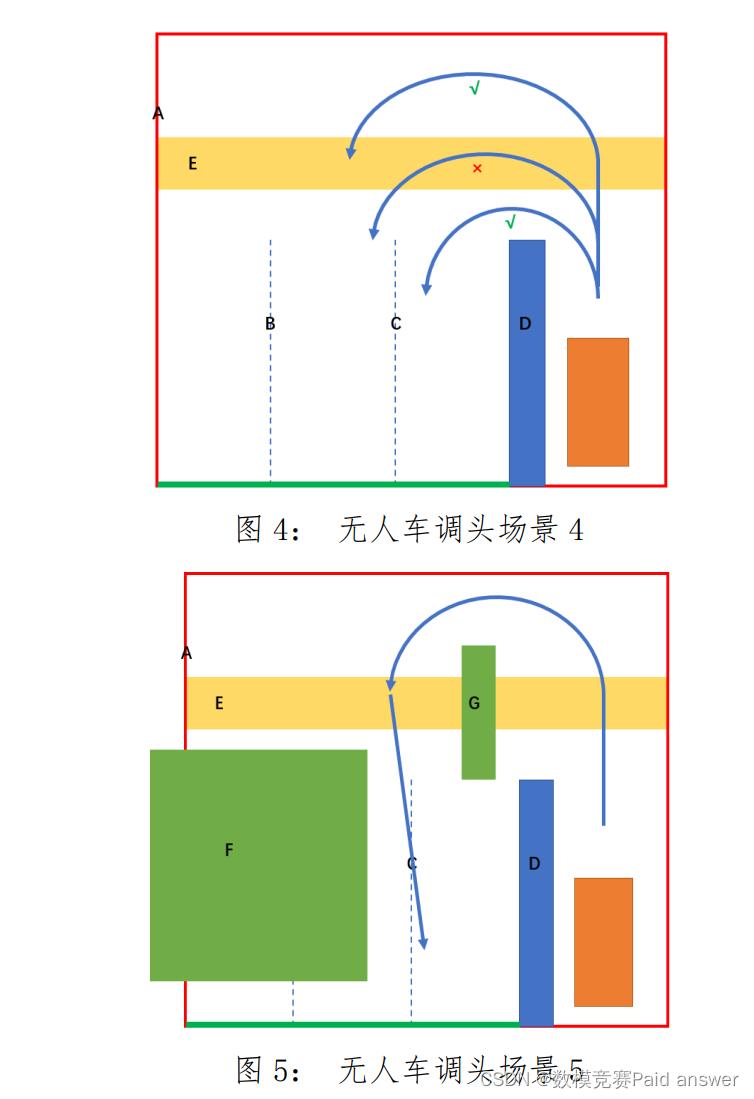
  问题 4：按交规规定，如果道路上存在人行横道即斑马线，其所占区域在附件数据文件中以 E 表示，则无人车需要尽可能在不压人行横道的情况下通过，如果无法做到，则需要越过（后轮越过）人行横道后再开始调头，禁止骑人行横道调头（如图 4 场景 4 所示）。其中标识“√”的为可行通行方式，标识“×”为骑人行道调头方式。建立相应的无人车调头的数学模型，给出合理的算法设计和相应的调头轨迹；当斑马线和障碍物同时存在时（如图 5 场景 5 所示），你的模型和算法如何同时满足交规并进行避障绕行？

  问题 5：无人车在实际路况行驶中进行调头时，道路中的障碍物通常是处于移动状态，如对向来车等，针对图 3 和图 5 的两种场景，假设图中标识的障碍物位置为无人车处在起始时刻的初始位置，障碍物以一定的速度移动，假设只考虑与道路平行方向移动，请建立更一般的无人车调头轨迹规划模型并给出相应算法设计和无人车调头策略，给出仿真结果。
  问题 6：为保证无人驾驶的安全性，无人车的轨迹规划算法必须拥有尽可能高的求解成功率（应倾向使用更收敛更稳定，失败率更低的计算方法）同时为了能对路况进行快速反应，需要以尽可能高的频率进行计算（计算复杂度尽量低）。你的算法如何在求解成功率和求解耗时这两方面优化？

问题分析：
  在交会几何和预测观测车辆行驶轨迹的前提下，我们构建了一个基于约束条件的轨迹模型。现有的控制算法是以点线式车辆-道路模型进行设计，忽略车辆与道路形状之间的实际差异，利用参数化曲线[5]表示道路轨迹，车辆根据参数化曲线以及自身状态做出转向动作。
  针对问题一：在基于交会几何和预测观测车辆行驶轨迹的前提下，结合车辆行驶动力学模型和转弯时的侧向动力模型，我们构建了一个基于约束条件的轨迹模型。其中，车辆侧向受力时，从车辆侧向、横摆两个自由度进行运动。而且车辆在转弯时，需考虑转弯半径、速度，安全距离等因素。由题设条件可知：加速度、车宽、车道宽度、传动比等为定值，所以我们采用界定分析法确定车辆行驶的轨迹区域，选取加速度、最大曲率、安全距离等作为约束条件，在已有的地图模型基础上建立轨迹预测模型，并用 MATLAB 中的 Automated Driving Toolbox进行仿真。只要运动轨迹满足界定区域 1、3 之间就可以完成避障且实现转弯。
  针对问题二：在问题一的基础上，已知曲率决定转弯半径，方向盘转角决定的是车转弯时轨迹半径的极限值。而车在转弯时，是否需要倒车的条件是由路宽、车距、最小曲率半径所决定的。这里，我们采用路径规划算法对轨迹进行预测，寻找其界限值。由题设条件可知，临界值由安全距离、最小半径、车宽三者共同决定。根据经验可知，当最小半径都不满足一次性转弯时，那么就必须倒车。同时，也将最小半径设为界定值。
  针对问题三：依据题干条件设定两个场景，场景一为仅存在 F 或 G 障碍物；场景二为障碍物 F、G 同时都存在。依据动力学原理，建立无人车运动的非完整约束模型和行驶过程中的速度约束方。基于障碍项、曲率项、光滑项、场函数构建损失函数，并将其作为优化对象。通过寻找约束条件进行非线性规划建模，并采用hybirdA算法实现其路径规划。
  针对问题四：利用问题二中得到的约束条件和附件数据计算出最小转弯半径，用 AutoCAD 建立地图模型。在此基础上，进一步判断当道路中存在人行道时，求解无人车不压线通过的临界值。通过路径规划法计算出无人车在满足安全距离、交规等约束条件下的最短路径，使用 MATLAB 进行仿真得到轨迹模型。基于问题三的优化模型和搜索方式，重置地图坐标。
  针对问题五：无人车避障主要是利用先进的传感技术来增强无人车的感知能力，将感知系统获取的车速、位置等实时信息反馈给系统，同时根据路况与车流的综合信息判断和分析潜在的安全隐患。依据题设条件，我们将来往车辆与无人车的速度进行归一化处理，即将来往车辆（动态障碍）与无人车间的速度差通过补偿，使其与动态障碍物处以一种相对静止的状态。此时，无人车的搜索路径便取决于距离障碍物的远近，由此建立障碍物位置变化约束方程。
  针对问题六：结合以上五个模型以及从算法复杂度和耗时率两方面考虑，分析其hybirdA算法的优点及局限性。

模型的建立与求解：
  转向条件
  保证无人车在转弯过程中，车轮与地面之间是纯滚动，需符合 Ackerman 转向方程：


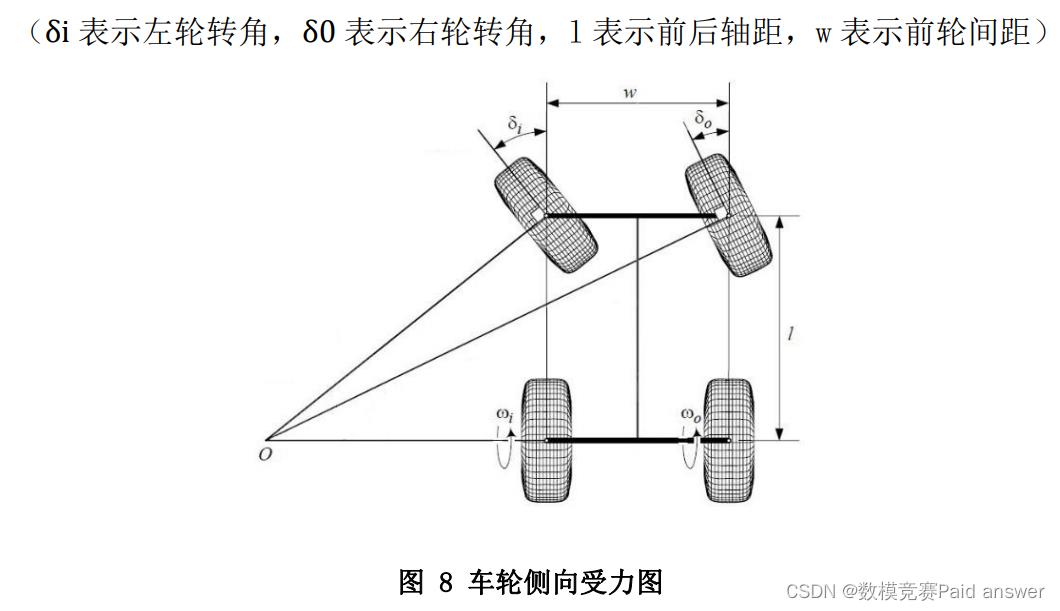
转弯几何原理
绘制出无人车转向过程中前轮摆角、车身结构和两后轮中心处轨迹半径以及整车重心处轨迹半径的几何关系，则有

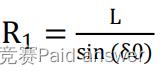
转向速度与转向加速度对转弯的影响：

基于上述条件，选取无人车两后轮连线的中点作为控制点，理由如下：
绘制无人车转弯过程如图 1 所示，将无人车后轮中点设为 Q，根据图中几何关系

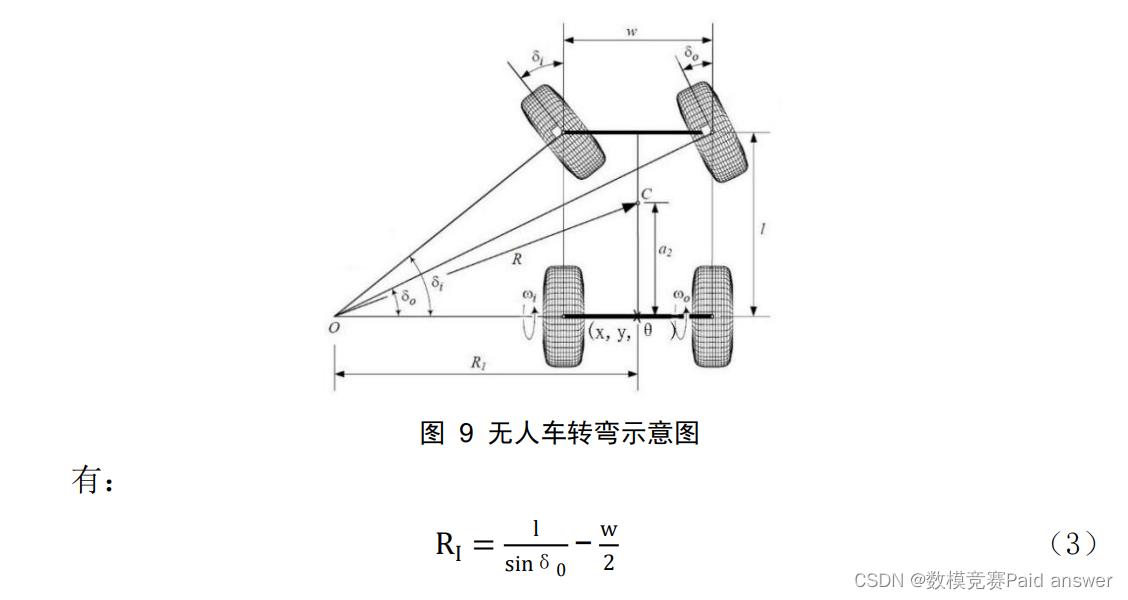
内外侧轮胎的转向半径不同，联立公式（1）和公式（3）得

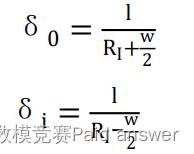
综上无人车行驶任意时刻的位置都可以用 Q 点的位置坐标和该点车身与水平方向的夹角θ来表示，因此选取 Q 为控制点。

选取 Q 点为控制点后，采用界定分析法来确定轨迹区域，即给出所有约束条件则在非约束区域就是无人车运动轨迹。

论文缩略图：

程序代码：

function [allData, scenario, sensor] = ds__4()
%ds__4 - Returns sensor detections
% allData = ds__4 returns sensor detections in a structure
% with time for an internally defined scenario and sensor suite. %
% [allData, scenario, sensors] = ds__4 optionally returns
% the drivingScenario and detection generator objects. % Generated by MATLAB(R) 9.8 (R2020a) and Automated Driving Toolbox 3.1 (R2020a). % Generated on: 18-Apr-2021 12:13:54
% Create the drivingScenario object and ego car
[scenario, egoVehicle] = createDrivingScenario;
% Create all the sensors
sensor = createSensor(scenario);
allData = struct('Time', , 'ActorPoses', , 'ObjectDetections', , 'LaneDetections', );
running = true;
while runnin

% Generate the target poses of all actors relative to the ego vehicle
poses = targetPoses(egoVehicle);
time = scenario.SimulationTime;
% Generate detections for the sensor
laneDetections = [];
[objectDetections, numObjects, isValidTime] = sensor(poses, time);
objectDetections = objectDetections(1:numObjects);
% Aggregate all detections into a structure for later use
if isValidTime
allData(end + 1) = struct( ... 'Time', scenario.SimulationTime, ... 'ActorPoses', actorPoses(scenario), ... 'ObjectDetections', objectDetections, ... 'LaneDetections', laneDetections); %#ok<AGROW>
end
% Advance the scenario one time step and exit the loop if the scenario is complete
running = advance(scenario);
end
% Restart the driving scenario to return the actors to their initial positions. restart(scenario);
% Release the sensor object so it can be used again. release(sensor);
%%%%%%%%%%%%%%%%%%%%
% Helper functions %
%%%%%%%%%%%%%%%%%%%%
% Units used in createSensors and createDrivingScenario
% Distance/Position - meters
% Speed - meters/second
% Angles - degrees
% RCS Pattern - dBsm
function sensor = createSensor(scenario)
% createSensors Returns all sensor objects to generate detections
% Assign into each sensor the physical and radar profiles for all actors
profiles = actorProfiles(scenario);
sensor = visionDetectionGenerator('SensorIndex', 1, ...
'SensorLocation', [4 0], ... 'MaxRange', 100, ... 'DetectorOutput', 'Objects only', ... 'Intrinsics', cameraIntrinsics([1814.81018227767 1814.81018227767],[320 240],[480
640]), ... 'ActorProfiles', profiles);
function [scenario, egoVehicle] = createDrivingScenario
% createDrivingScenario Returns the drivingScenario defined in the Designer
% Construct a drivingScenario object. scenario = drivingScenario;
% Add all road segments
roadCenters = [31.476 -5 0;
0 -5 0];
laneSpecification = lanespec(3, 'Width', 3.4872);
road(scenario, roadCenters, 'Lanes', laneSpecification);
roadCenters = [31.476 -12.507 0;
0 -12.507 0];
laneSpecification = lanespec(1, 'Width', 4.5517);
road(scenario, roadCenters, 'Lanes', laneSpecification);
% Add the actors
actor(scenario, ... 'ClassID', 5, ... 'Length', 16.0256, ... 'Width', 1.5434, ... 'Height', 0.8, ... 'Position', [8.12 -11.05 0.01], ... 'PlotColor', [0 114 189] / 255);
actor(scenario, ... 'ClassID', 5, ... 'Length', 4.9, ... 'Width', 4.9998, ... 'Height', 0.8, ... 'Position', [-171.8 46.5 0], ... 'PlotColor', [0 255 0] / 255);
actor(scenario, ... 'ClassID', 5, ... 'Length', 8.2223, ...
'Width', 1.8998, ... 'Height', 0.8, ... 'Position', [-169.7 -11 0], ... 'PlotColor', [0 255 0] / 255);
% Add the ego vehicle
egoVehicle = vehicle(scenario, ... 'ClassID', 1, ... 'Length', 5, ... 'Width', 2, ... 'Position', [5.89 -13.39 0.01], ... 'PlotColor', [0.85 0.325 0.098]);
waypoints = [5.89 -13.39 0.01;
13.62 -13.46 0.01;
16.25 -13.46 0.01;
19.51 -13.11 0.01;
26.74 -10.41 0.01;
27.31 -9.14 0.01;
27.31 -7.72 0.01;
26.67 -6.02 0.01;
25.18 -4.46 0.01;
22.84 -3.32 0.01;
20.36 -3.11 0.01;
17.81 -3.96 0.01;
14.62 -6.16 0.01;
11.99 -7.36 0.01;
7.95 -8.21 0.01;
3.27 -8.21 0.01;
0.15 -8.21 0.01; -3.04 -8.21 0];
speed = 30;
trajectory(egoVehicle, waypoints, speed);
vehicle(scenario, ... 'ClassID', 1, ... 'Length', 4.9, ... 'Width', 4.9998, ... 'Position', [9.51 -2.19 0.01], ... 'PlotColor', [0.929 0.694 0.125])
vehicle(scenario, ... 'ClassID', 1, ... 'Length', 8.2223, ... 'Width', 1.8998, ...
'Position', [17.03 -8.15 0.01], ... 'PlotColor', [0.494 0.184 0.556]);
function [allData, scenario, sensor] = ds__4()
%ds__4 - Returns sensor detections
% allData = ds__4 returns sensor detections in a structure
% with time for an internally defined scenario and sensor suite. %
% [allData, scenario, sensors] = ds__4 optionally returns
% the drivingScenario and detection generator objects. % Generated by MATLAB(R) 9.8 (R2020a) and Automated Driving Toolbox 3.1 (R2020a). % Generated on: 18-Apr-2021 12:16:07
% Create the drivingScenario object and ego car
[scenario, egoVehicle] = createDrivingScenario;
% Create all the sensors
sensor = createSensor(scenario);
allData = struct('Time', , 'ActorPoses', , 'ObjectDetections', , 'LaneDetections', );
running = true;
while running
% Generate the target poses of all actors relative to the ego vehicle
poses = targetPoses(egoVehicle);
time = scenario.SimulationTime;
% Generate detections for the sensor
laneDetections = [];
[objectDetections, numObjects, isValidTime] = sensor(poses, time);
objectDetections = objectDetections(1:numObjects);
% Aggregate all detections into a structure for later use
if isValidTime
allData(end + 1) = struct( ... 'Time', scenario.SimulationTime, ... 'ActorPoses', actorPoses(scenario), ... 'ObjectDetections', objectDetections, ... 'LaneDetections', laneDetections); %#ok<AGROW>
end
% Advance the scenario one time step and exit the loop if the scenario is complete
running = advance(scenario);
end