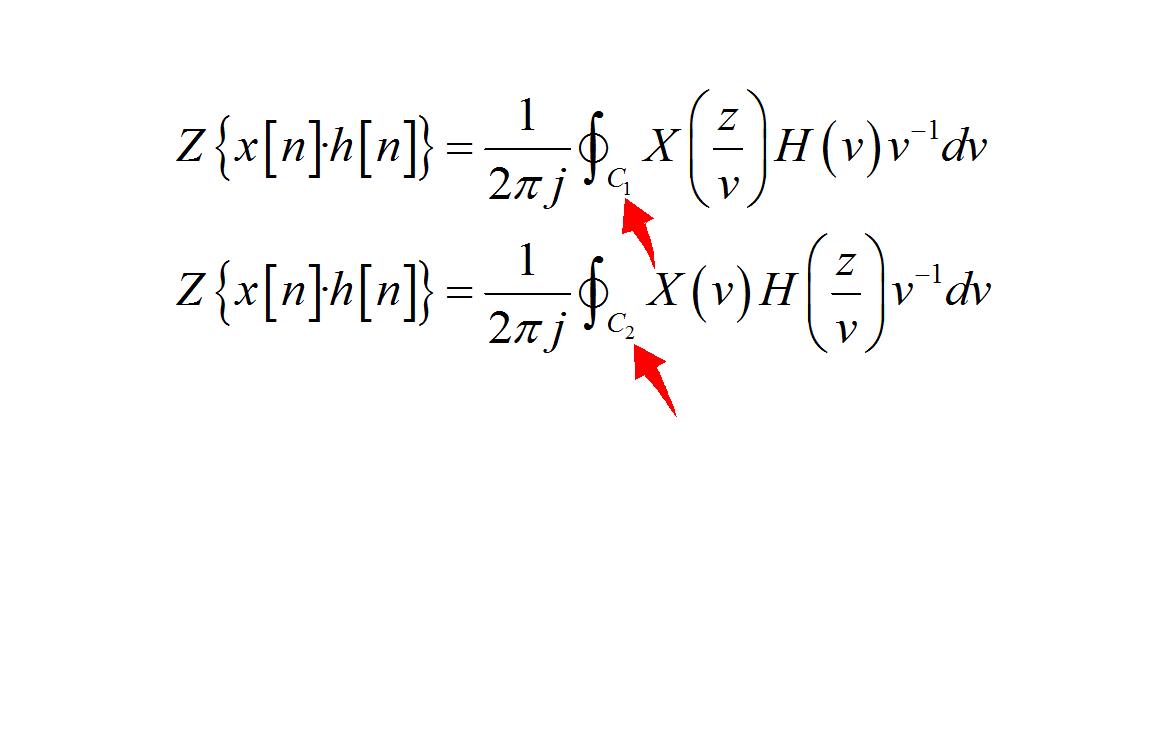SS2022-Z变换-性质-两个序列乘积的Z变换是什么？

Posted 2022-05-16 卓晴

简 介： 本文给出了z变换中最为复杂的 z域卷积定理及其应用。

关键词： 信号与系统，z变换，序列相乘，z域卷积

z变换序列乘积定理

 

§01 z域卷积

---

  z变换中，序列相乘定理， 也称z域卷积定理是这学期我们学习所有变换中 最为奇特和复杂的定理。 它描述了两个序列相乘结果的z变换 与它们各自z变换之间的关系。 下面让我们来看一下这个神奇的定理。

一、定理内容

已知两序列， $x\left[n\right],h\left[n\right]$，其中 $z$ 变换为$$Zx\left[n\right]=X\left(z\right),\left(R_{x1}<\left|z\right|<R_{x2}\right)$$$$Zh\left[n\right]=H\left(z\right),\left(R_{h1}<\left|z\right|<R_{h2}\right)$$则 $$Zx\left[n\right]\cdot h\left[n\right]=\frac{1}{2\pi j}{\oint }_{C_1}X\left(\frac{z}{v}\right)H\left(v\right)v^{-1}dv$$ 或者 $$Zx\left[n\right]\cdot h\left[n\right]=\frac{1}{2\pi j}{\oint }_{C_2}X\left(v\right)H\left(\frac{z}{v}\right)v^{-1}dv$$ 式中 $C_1,C_2$ 分别是 $X\left(\frac{z}{v}\right)$ 与 $H\left(v\right)$ ，或者 $X\left(v\right)$ 与 $H\left(\frac{z}{v}\right)$ 收敛域重叠区域内逆时针旋转围线。而 $Zx\left[n\right]\cdot h\left[n\right]$ 的收敛域是 $X\left(v\right)$ 与 $H\left(\frac{z}{v}\right)$ ，或者 $X\left(\frac{z}{v}\right)$ 与 $H\left(v\right)$ 的重叠部分。即 $$R_{x1}{R}_{h1}<\left|z\right|<R_{x2}{R}_{h2}$$

  定理的内容为： 对于两个序列x[n],h[n]， 它们具有各自的z变换， 以及对应的收敛域。 那么两个序列的乘积对应的z变换有两种等效形式： 一种是上面这个表达式， 另外一种是下面的这种表达式。 它们的区别是函数变量发生了改变。 对比一下，可以看出， 这两种表达式本质上是将X(z)与H(z)进行对调。 这与x[n],h[n]在时域相乘具有交换性是相通的。

  看完这个定理内容，我们有三个疑惑： （1）在FT，LT中都有时域信号相乘， 对应变换域内信号卷积。 为什么z变换的序列乘积定理显得与卷积没有毛关系呢？  （2）在其它z变换定理中， 比如序列线性，卷积定理中， 结果收敛域都是参与运算序列z变换收敛域的交集， 但序列相乘则出现这样奇怪的关系。  （3）这个围线积分中的路径C1,C2如何进行确定呢？

  以上问题都可以通过定理的证明来进行回答。 下面我们先看看定理证明过程。

二、定理证明

  对于序列乘积定