SS2022-Z变换-性质-Z变换中的线性和指数加权性质是什么？
Posted 卓晴
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了SS2022-Z变换-性质-Z变换中的线性和指数加权性质是什么？相关的知识，希望对你有一定的参考价值。
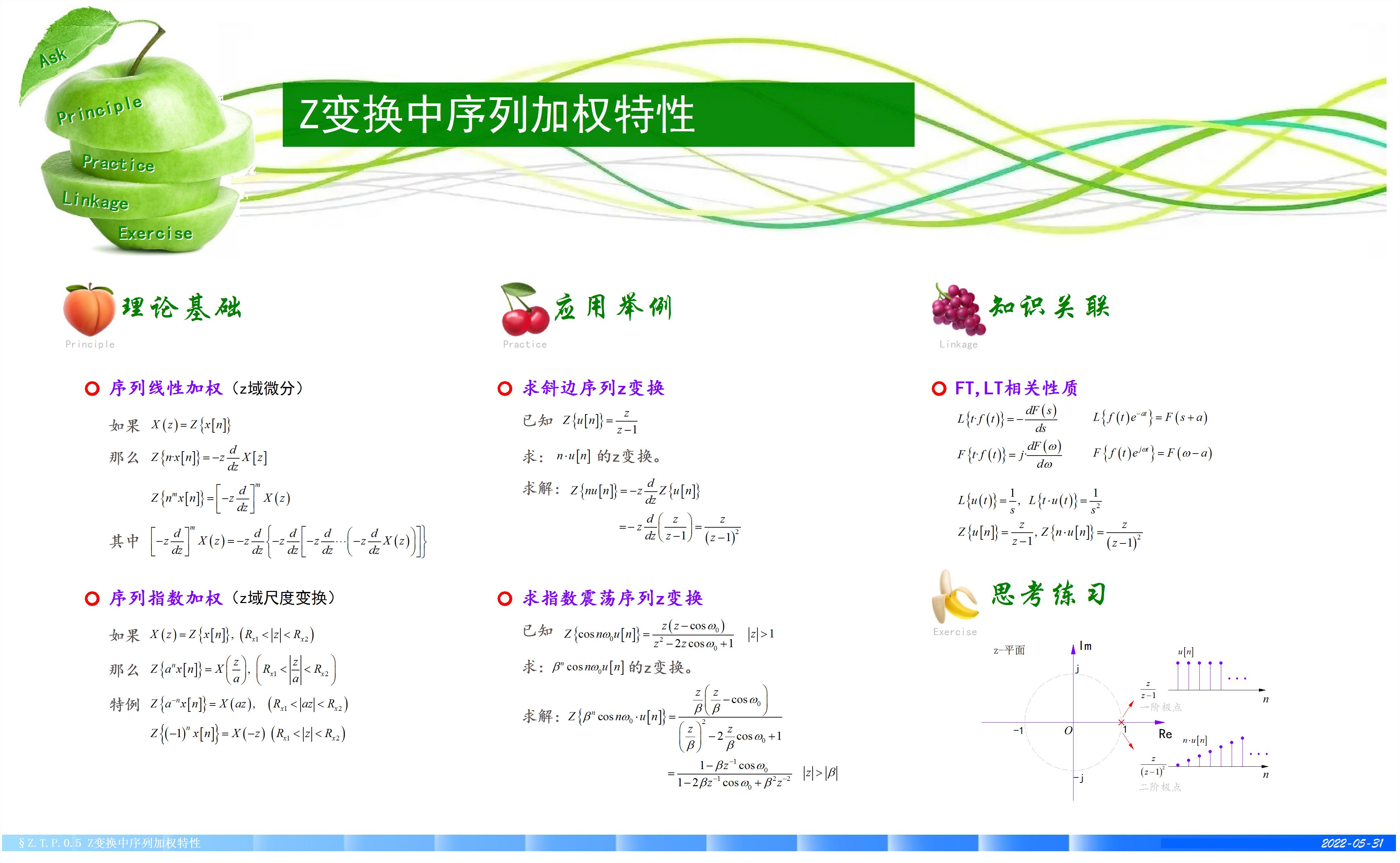
简 介： 本文给出了z变换的线性与指数加权特性。
关键词： ZT，线性加权，指数加权
§01 数学原理
z变换中序列的加权特性包 含着线性加权和指数加权特性。
1.1 序列线性加权
Z变换序列线性加权性质，也称为 z 域微分性质。
如果
X
(
z
)
=
Z
x
[
n
]
X\\left( z \\right) = Z\\left\\ x\\left[ n \\right] \\right\\
X(z)=Zx[n] 那么
Z
n
⋅
x
[
n
]
=
−
z
d
d
z
X
[
z
]
Z\\left\\ n \\cdot x\\left[ n \\right] \\right\\ = - zd \\over dzX\\left[ z \\right]
Zn⋅x[n]=−zdzdX[z]
Z
n
m
x
[
n
]
=
[
−
z
d
d
z
]
m
X
(
z
)
Z\\left\\ n^m x\\left[ n \\right] \\right\\ = \\left[ - zd \\over dz \\right]^m X\\left( z \\right)
Znmx[n]=[−zdzd]mX(z) 其中
[
−
z
d
d
z
]
m
X
(
z
)
=
−
z
d
d
z
−
z
d
d
z
[
−
z
d
d
z
⋯
(
−
z
d
d
z
X
(
z
)
)
]
\\left[ - zd \\over dz \\right]^m X\\left( z \\right) = - zd \\over dz\\left\\ - zd \\over dz\\left[ - zd \\over dz \\cdots \\left( - zd \\over dzX\\left( z \\right) \\right) \\right] \\right\\
[−zdzd]mX(z)=−zdzd−zdzd[−zdzd⋯(−zdzdX(z))]
z变换中序列线性加权特性，也称z变换的z域微分性质。对于序列 x[n]，每一项分别乘以自变量 n，即自变量的一次多项式， 这个过程称为线性加权。那么加权后序列的 z 变换是 对原序列的 z 变换求导之后，再乘以 -z 。
这个性质可以推广到 对序列 使用 n 的 m 次方加权， 对应的 z 变换就是原序列的 z 变换进行 m 次求导和乘以 -z 。
证明过程也比较简单。 直接对 z 变换的公示 X ( z ) = ∑ n = − ∞ + ∞ x [ n ] z − n X\\left( z \\right) = \\sum\\limits_n = - \\infty ^ + \\infty x\\left[ n \\right]z^ - n X(z)=n=−∞∑+∞x[n]z−n 两边同时对 z 进行求导， 然后交换累加和求导 d X ( z ) d z = d d z ∑ n = − ∞ + ∞ x [ n ] z − n = ∑ n = − ∞ + ∞ x [ n ] d d z ( z − n ) dX\\left( z \\right) \\over dz = d \\over dz\\sum\\limits_n = - \\infty ^ + \\infty x\\left[ n \\right]z^ - n = \\sum\\limits_n = - \\infty ^ + \\infty x\\left[ n \\right]d \\over dz\\left( z^ - n \\right) dzdX(z)=dzdn=−∞∑+∞x[n]z−n=n=−∞∑+∞x[n]dzd(z−n) = ∑ n = − ∞ + ∞ x [ n ] ( − n ) z − n − 1 = − z − 1 ∑ n = − ∞ + ∞ x [ n ] z − n = \\sum\\limits_n = - \\infty ^ + \\infty x\\left[ n \\right]\\left( - n \\right)z^ - n - 1 = - z^ - 1 \\sum\\limits_n = - \\infty ^ + \\infty x\\left[ n \\right]z^ - n =n=−∞∑+∞x[n](−n)z−n−1=−zSS2022-Z变换-性质-两个序列乘积的Z变换是什么？