SS2022-Z变换-性质-什么是ZT线性性质？

Posted 2022-05-16 卓晴

简 介： 本节内容介绍了z变换的线性特性及其应用。灵活定理虽然简单， 灵活掌握应用是关键。

关键词： ZT，线性性质

 

§01 数学原理

---

z变换的线性特性比较简单， 用途比较广泛， 也是其他特性的基础。 下面我们进行介绍。

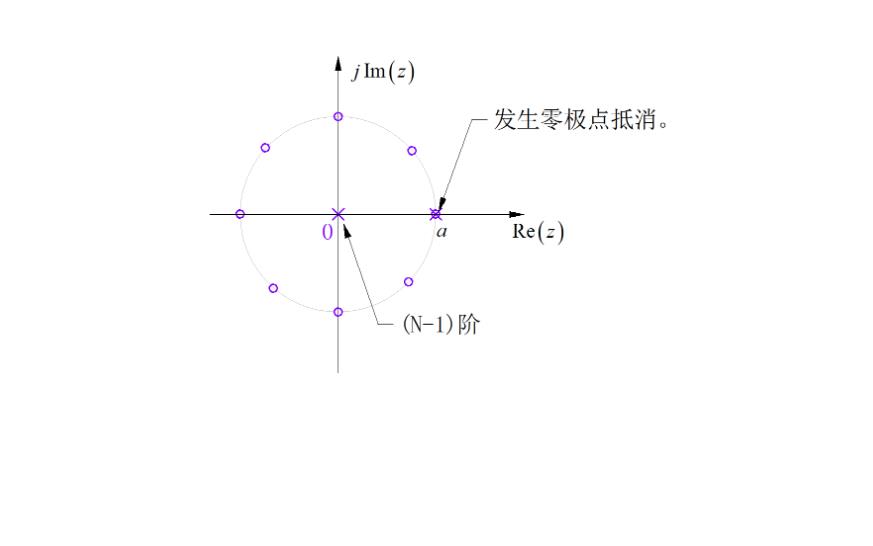
z变换是线性变换， 满足叠加性与齐次性：$$Zx\left[n\right]=X\left(z\right),\left(R_{x1}<\left|z\right|<R_{x2}\right)$$$$Zy\left[n\right]=Y\left(z\right),\left(R_{y1}<\left|z\right|<R_{y2}\right)$$那么 $$Zax\left[n\right]+by\left[n\right]=aX\left(z\right)+bY\left(z\right),\left(R_1<\left|z\right|<R_2\right)$$ 通常情况下 $R_1=\max \left(R_{x1},R_{y1}\right),R_2=\min \left(R_{x2},R_{y2}\right)$ ，即线性叠加信号z变换的收敛域是参与运算信号z变换收敛域的交集。 但叠加后z变换如果出现零极点抵消，那么收敛域有可能扩大。

z变换是线性变换， 满足叠加性与齐次性： 可以表述为序列的线性组合的z变换， 等于各自信号z变换的线性组合。 线性叠加信号z变换的收敛域是 参与运算信号z变换收敛域的交集。  但叠加后z变换如果出现零极点抵消， 那么收敛域有可能扩大。 这部分后面会通过举例进行说明。
  

 

§02 应用举例

---

下面给出两个基本应用举例。

2.1 双曲余弦和正弦

第一个例子是求双曲余弦和正弦的z变换。 这是双曲余弦和正弦的定义表达式， 它们都是两个指数序列的叠加。 所以根据z变换的线性特性， 可以先求取两个单边指数序列的z变换， 然后再将它们叠加在一起。

  求双曲余弦和双曲正弦的z变换：$$x_c\left[n\right]=\cosh \left(n{\omega }_0\right)u\left[n\right]=\frac{e^{n{\omega }_0}+e^{-n{\omega }_0}}{2}u\left[n\right]$$$$x_s\left[n\right]=\sinh \left(n{\omega }_0\right)u\left[n\right]=\frac{e^{n{\omega }_0}-e^{-n{\omega }_0}}{2}u\left[n\right]$$

◎ 求解： 根据单边指数序列 $a^{n}u\left[n\right]$ 的z变换的表达式 $z/\left(z-a\right),\left|z\right|>\left|a\right|$ ，所以 Z e n ω 0 u [ n ] = z z − e ω 0 ,     ( ∣ z ∣ > ∣ e