数字信号处理傅里叶变换性质 ( 共轭对称与共轭反对称图像示例 | 实序列中共轭对称是偶对称 | 实序列中共轭反对称是奇对称 )

Posted 2022-03-17 韩曙亮

文章目录

• 一、共轭对称与共轭反对称图像示例
• • 1、共轭对称序列图示
  • 2、共轭反对称序列图示
  • 3、总结

一、共轭对称与共轭反对称图像示例

---

序列 $x(n)=0.8^{n}u(n)$ , 取 $0$ ~ $10$ 之间的 11 个点 , 绘制后样式如下 :

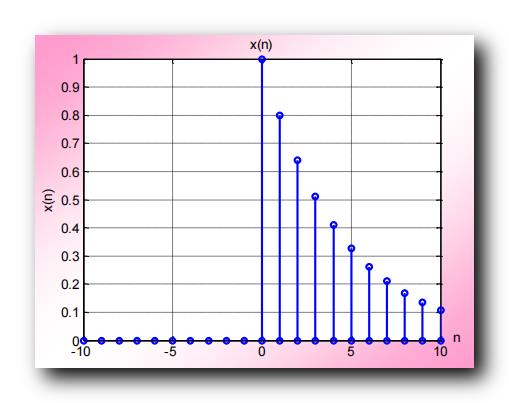
1、共轭对称序列图示

共轭对称序列概念 :

对于 序列 $x(n)$ , 如果 $x(n)$ 共轭 $x(-n)$ ,

$$x(n)=x^{\ast }(-n)$$

则称 $x(n)$ 是 关于原点 的 共轭对称序列 , 记做

$$x_e(n)$$

其中 , $-\infty <n<+\infty$ ;

$x(n)$ 的共轭对称序列 $x_e(n)$ 图像如下 : 对于 实序列 来说 , 共轭对称 就是 偶对称 ;

原序列有 $n=11$ 个点 , 其共轭对称序列 ( 偶对称序列 ) 有 $2n-1=21$ 个点 ;

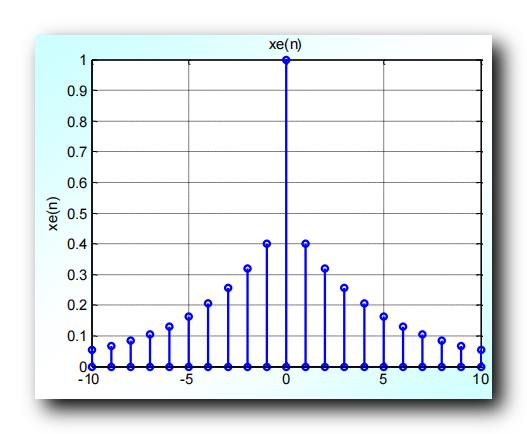
2、共轭反对称序列图示

共轭反对称序列概念 :

对于 序列 $x(n)$ , 如果 ,

$$x(n)=-x^{\ast }(-n)$$

成立 , 则称 $x(n)$ 是 关于原点 的 共轭反对称序列 , 记做

$$x_o(n)$$

其中 , $-\infty <n<+\infty$ ;

$x(n)$ 的共轭反对称序列 $x_o(n)$ 图像如下 : 对于 实序列 来说 , 共轭反对称 就是 奇对称 ;

原序列有 $n=11$ 个点 , 其共轭反对称序列 ( 奇对称序列 ) 有 $2n-1=21$ 个点 ;

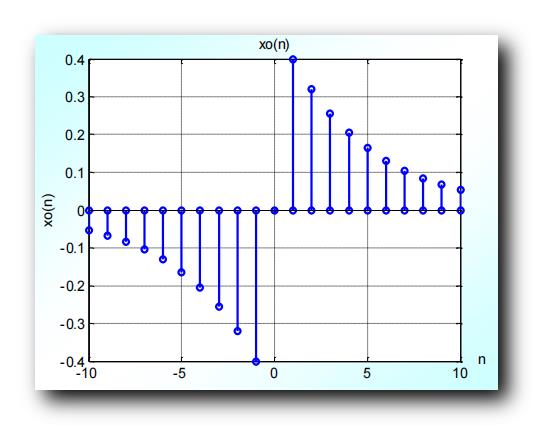
3、总结

实序列 :

• 偶对称 : $x(n)=x(-n)$
• 奇对称 : $x(n)=-x(-n)$

复序列 :

• 共轭对称 : $x(n)=x^{\ast }(-n)$
• 共轭反对称 : $x(n)=-x^{\ast }(-n)$

对于 实序列 来说 , 共轭对称 就是 偶对称 ;

对于 实序列 来说 , 共轭反对称 就是 奇对称 ;