一只青蛙从正三角形的顶点a 出发，每次随机地跳到另一个顶点处，则它跳了5次，正好跳回a处的概率

Posted 2023-04-09

我没有什么太好的思路，说出来大家指正
1、纯粹用推演法，结果是5/16
2、分析可知，第一步跳到非a点，最后一步是从非a点跳回a点（此步概率为1/2），中间三步用推演法(非a点三步跳到非a点，推演出概率是5/8)，总概率也是5/16
3、如果把青蛙连续跳5步的过程看做一个排列，那这种排列一共有2^5=32种，其中有10种是落在a点，概率就是10/32=5/16。从上一个朋友的推演过程发现，如果是跳4步，排列有16种，落回起跳点的次数是6；跳3步排列有8种，回起跳点的次数是2；跳2步排列有4种，回起跳点次数是2；跳1步排列有2种，回起点数为0。所以我推测跳奇数步回起跳点的次数是 总排列数除以3的商(取整)，跳偶数步回起跳点的次数是 总排列数除以3的商(取整)+1 。简单分析，如果某一步跳到a的次数少1，那么下一步跳到b和c的次数就会各少1，相对的跳到a的次数要多1。这步多下步少，这步少下步多。用这个思路的话，如果青蛙是跳四边形，五边形，甚至n边形都可以分析得结果。 参考技术A 可题可化为从正三角形的A点出发，跳4次后能回到B处的可能性，可作树形图
次数 A
1 B C
2 A C A B
3 B C A B B C A C
4 AC AB BC AC AC AB BC AB
共有16种可能，满足条件的有5种，故为5/16

求下面数学题的推套过程！

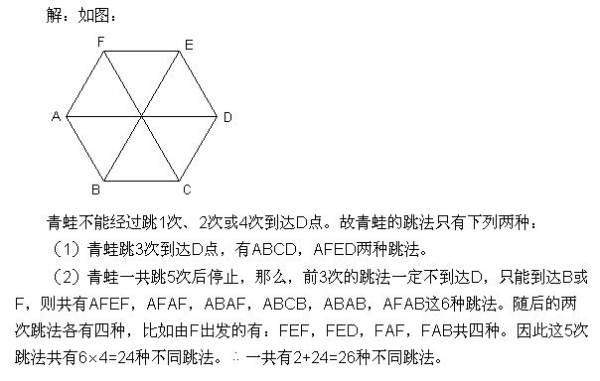
设为正六边形，一只青蛙开始在顶点处，它每次要随意跳到相邻两个顶点之一，若在5次之内跳到点，则停止跳动；若5次之内不能到达点，则跳完5次也停止跳动，那么这只青蛙从开始到停止，可能出现的不同跳法总数共有几种？

答案：26种。求为什么！
谢谢！
一只青蛙开始在顶点A处
若在5次之内跳到点D
若5次之内不能到达点D

标准答案来了青蛙不能经过跳1次、2次或4次到达D点。故青蛙的跳法只有下列两种： （1）青蛙跳3次到达D点，有ABCD，AFED两种跳法。 （2）青蛙一共跳5次后停止，那么，前3次的跳法一定不到达D，只能到达B或F，则共有AFEF，AFAF，ABAF，ABCB，ABAB，AFAB这6种跳法。随后的两次跳法各有四种，比如由F出发的有：FEF，FED，FAF，FAB共四种。因此这5次跳法共有6*4=24种不同跳法。一共有2+24=26种不同跳法。然后看这里，有图片http://hi.baidu.com/xiaozhaotaitai/album/item/17c147fae059c9999f51460f.html

参考技术A 跳到点是什么意思？