求下面数学题的推套过程！

Posted 2023-04-09

设为正六边形，一只青蛙开始在顶点处，它每次要随意跳到相邻两个顶点之一，若在5次之内跳到点，则停止跳动；若5次之内不能到达点，则跳完5次也停止跳动，那么这只青蛙从开始到停止，可能出现的不同跳法总数共有几种？

答案：26种。求为什么！
谢谢！
一只青蛙开始在顶点A处
若在5次之内跳到点D
若5次之内不能到达点D

标准答案来了青蛙不能经过跳1次、2次或4次到达D点。故青蛙的跳法只有下列两种： （1）青蛙跳3次到达D点，有ABCD，AFED两种跳法。 （2）青蛙一共跳5次后停止，那么，前3次的跳法一定不到达D，只能到达B或F，则共有AFEF，AFAF，ABAF，ABCB，ABAB，AFAB这6种跳法。随后的两次跳法各有四种，比如由F出发的有：FEF，FED，FAF，FAB共四种。因此这5次跳法共有6*4=24种不同跳法。一共有2+24=26种不同跳法。然后看这里，有图片http://hi.baidu.com/xiaozhaotaitai/album/item/17c147fae059c9999f51460f.html

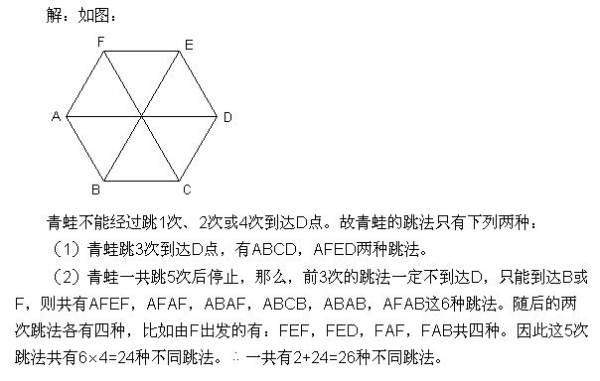
参考技术A 跳到点是什么意思？

非亏损矩阵的问题求解答

为何实对称矩阵都是非亏损矩阵？求证明过程

n阶矩阵A若有n个线性无关的特征向量，称A为非亏损矩阵，即A有完备的线性无关的特征向量系。反之称A为亏损矩阵。
在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合 ，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。
矩阵是高等代数学中的常见工具，也常见于统计分析等应用数学学科中。在物理学中，矩阵于电路学、力学、光学和量子物理中都有应用；计算机科学中，三维动画制作也需要用到矩阵。 矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。
这是我找到的 望采纳~O(∩_∩)O~ 参考技术A 找本教材，把实对称矩阵可以正交对角化的部分看一遍追问

你这个答案我是不会把财富给你的....

追答

随便你，反正我不在乎