离散数学中传递闭包怎么求 通俗一点

Posted 2023-04-29

离散数学中传递闭包怎么求 通俗一点

方法：warshall法，即运行n次，每次使得MR[n][i],MR[i][n]都为1时使得MR[i][j]为1,否则还是为MR[i][j]。
传递闭包的计算过程一般可以用Warshell算法描述：
For 每个节点i Do
For 每个节点j Do
If j能到i Then
For 每个节点k Do
a[j, k] := a[j, k] Or ( a[j, i] And a[ i, k] )
其中a数组为布尔数组，用来描述两个节点是否相连，可以看做一个无权图的邻接矩阵。算法过程跟Floyd很相似，三重循环，枚举每个中间节点。不过传递闭包只需要求出两个节点是否相连，而不用求其间的最短路径长。
传递性：对于一个节点i，如果j能到i，i能到k，那么j就能到k。求传递闭包，就是把图中所有满足这样传递性的节点都弄出来，计算完成后，就知道任意两个节点之间是否相连。
传递闭包的定义：R’是R（不具有传递性质）变动最少的步骤得到的具有传递性质的关系。
扩展资料
算法实例：
#include<stdio.h>
#define
N
10
int
judge(int
k,int
i,int
j)

if(i==1
&&
j==1)
return
1;

return
k;

void
warShall(int
MR[N][N],int
n)

for(int
k=0;k<n;k++)
for(int
i=0;i<n;i++)
for(int
j=0;j<n;j++)
if(i!=k
||
j!=k)
MR[i][j]=judge(MR[i][j],MR[k][j],MR[i][k]);





int
main()

int
MR[10][10];
int
mul;
scanf("%d",&mul);
for(int
i=0;i<mul;i++)
for(int
j=0;j<mul;j++)
scanf("%d",&MR[i][j]);


printf("求传递闭包为:\n");
warShall(MR,mul);
for(int
i=0;i<mul;i++)
for(int
j=0;j<mul;j++)
printf("%d
",MR[i][j]);

printf("\n");

return
0;

运行结果：
参考资料：百度百科-传递闭包 参考技术A 自反闭包，是在原关系基础上，加上所有自反关系。
类似地，传递闭包，是在原关系基础上，补充符合传递性要求的关系。
对称闭包，是在原关系基础上，补充符合对称性要求的关系。

离散数学如何求补元

最近看自考得离散数学，看到求补元那段，单看书上的定义，纯懵逼的，找了两个晚上的资料，终于找到通俗易懂的求补元的方法了。

首先，通俗易懂的方法来自于：https://m.wenda.so.com/q/1535676852215544

 

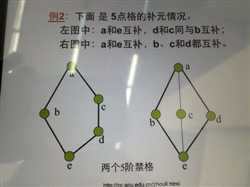
左图，a是最大元，e是最小元。最大元与最小元互为补元。求其余元素的补元时，若A与B互为补元，从图中看就是，从这两个点出发的路径，向上只相交于最大元，向下只相交于最小元。这里b与c，b与d都可以做到这一点。
右图，b与c，b与d，c与d也都满足这一点。

 

 红色标粗部分，通俗点的意思是，两个点画线出发，只会存在两个交点，分别是最大元和最小元，如果存在其他非最大最小元交点，则不是补元。

佐证该判断方法，请看百度百科：https://baike.baidu.com/item/%E6%9C%89%E8%A1%A5%E6%A0%BC/2203999?fr=aladdin

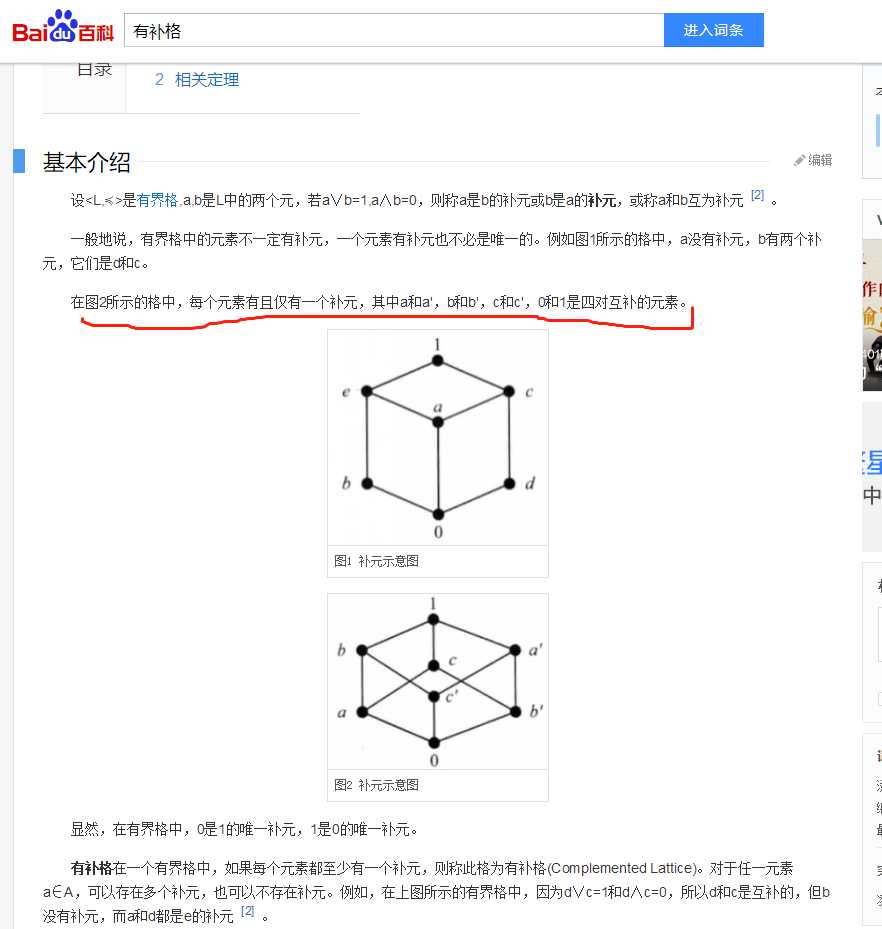
这里的图2佐证了上面的判断方法的正确性。

比如c与a，除了有交于最大最小元的交点，还存在其他的交点，如b，b‘，a’等交点。