无痛理解傅里叶变换
Posted Jie Qiao
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了无痛理解傅里叶变换相关的知识,希望对你有一定的参考价值。
连续傅里叶变换
对于任意的一个函数
f
(
t
)
\\displaystyle f( t)
f(t):
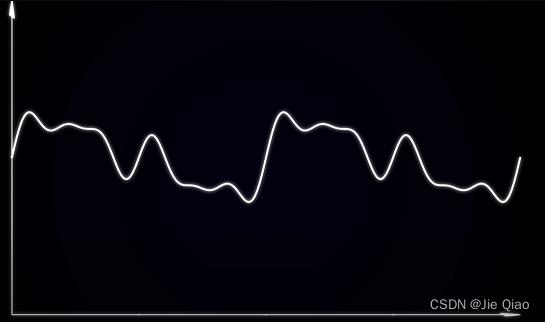
它往往可以被分解成多个不同的频率下sin cos 函数的组合:
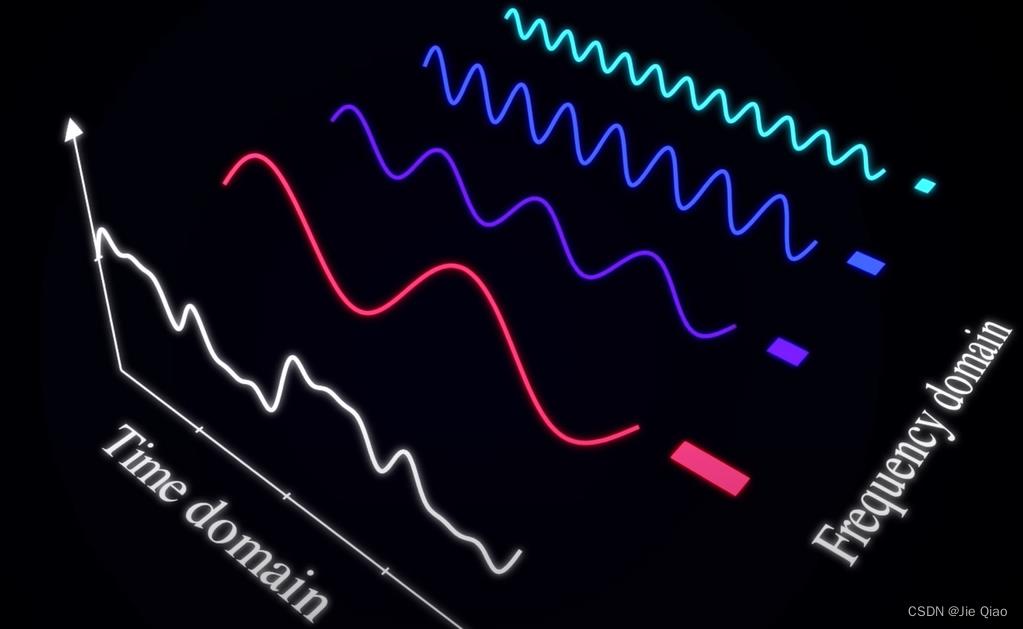
所以为了去捕捉每个不同频率下的sin cos的“成分”,一个直观的想法就是,对于每个频率 w \\displaystyle w w,我们分别计算 s i n ( w t ) \\displaystyle sin( wt) sin(wt)函数和 c o s ( w t ) \\displaystyle cos( wt) cos(wt)函数与目标函数的“相似度”,而这个相似度可以用内积来计算:
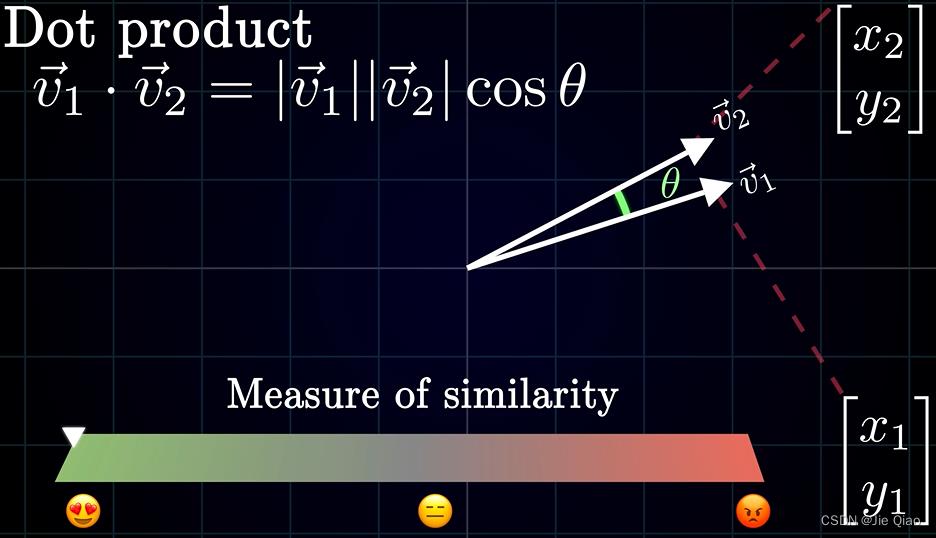
内积越大则意味着他们越相似,既然如此,一个直观的想法就是去计算:
F s i n ( w ) = ∫ f ( t ) sin ( w t ) d t F c o s ( w ) = ∫ f ( t ) cos ( w t ) d t F_sin( w) =\\int f( t)\\sin( wt) dt\\\\ F_cos( w) =\\int f( t)\\cos( wt) dt Fsin(w)=∫f(t)sin(wt)dtFcos(w)=∫f(t)cos(wt)dt
这里 F s i n ( w ) \\displaystyle F_sin( w) Fsin(w)其实就表示这个函数 f \\displaystyle f f与频率为 w \\displaystyle w w的sin函数的相似性。
我们可以看个直观的例子,考虑函数
y
=
s
i
n
(
x
)
+
c
o
s
(
3
x
)
y=sin(x)+cos(3x)
y=sin(x)+cos(3x)
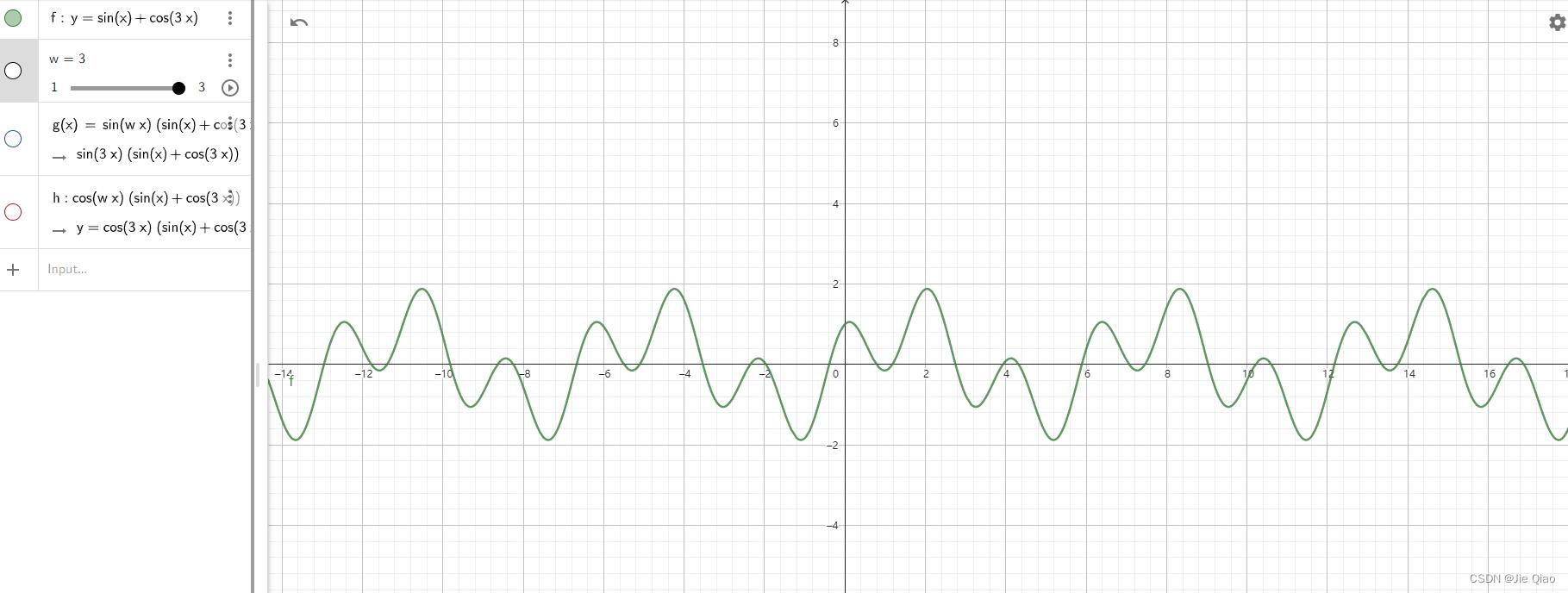
如果我们分别计算在不同频率下f(x)与sin(wx)函数的相乘,那么这条曲线是长这样的(蓝色的线=f(x)*sin(wx)):
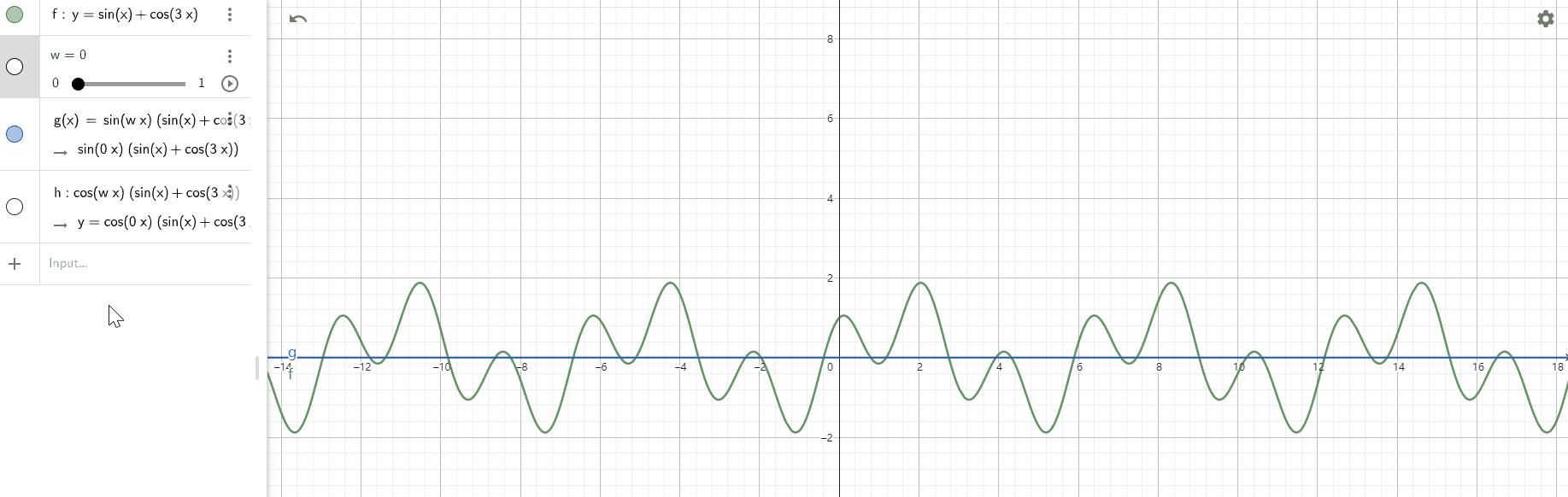
显然,我们计算的相似度其实就是这条蓝色线的面积之和,可以发现在恰好w=1的时候,这条曲线面积加起来是最大的!

所以傅里叶变换的本质就是在捕捉不同频率下与f(t)函数的相似性。
类似的对于cos函数,红色的线=f(x)cos(wx):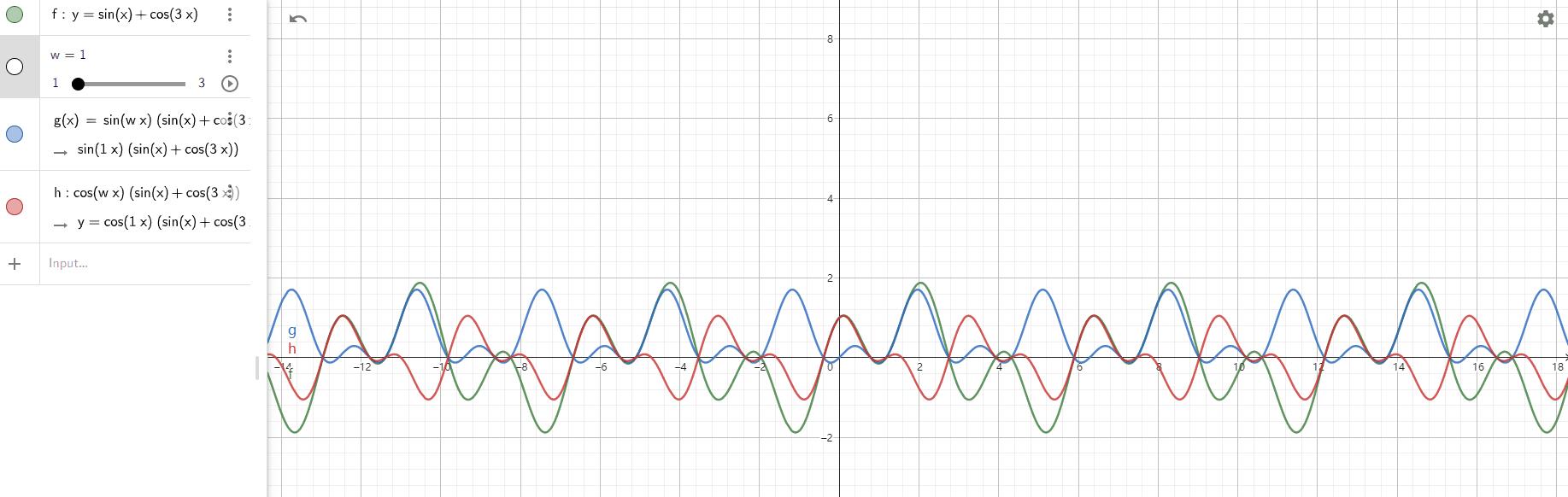
显然当w=3的时候,红色的线的面积之和也达到了最大:

根据傅里叶级数,任意的函数都可以被sin和cos函数表示,那有没有一种办法,同时计算sin和cos两种相似性呢?答案是可以,我们可以用复数来实现!
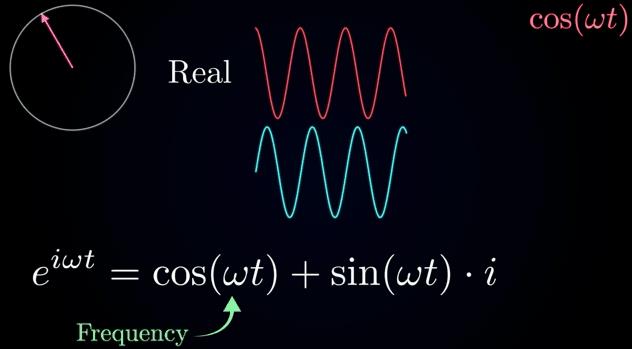
根据欧拉公式, e i w t \\displaystyle e^iwt eiwt其实可以分解成cos和sin两项,所以我们只需要计算
F ( w ) = ∫ f ( t ) e i w t d t F( w) =\\int f( t) e^iwt dt F(w)=∫f(t)eiwtdt
这个其实就是一个傅里叶变换了(出于传统习惯,我们一般会用 e − i w t \\displaystyle e^-iwt e−iwt,但其实这并不影响的),所以实数项就是与cos函数的相似度,虚数项就是与sin函数的相似度。
离散傅里叶变换
离散傅里叶变换其实就是考虑 f ( t ) \\displaystyle f( t) f(t)的采样点,比如我们有 f ( t 1 ) , f ( t 2 ) , f ( t 3 ) , f ( t 4 ) f( t_1) ,f( t_2) ,f( t_3) ,f( t_4) f(t1),f(t2),f(t3),f(t4) 这4个点,那么离散傅里叶变换会认为这个 t = 0 , 1 , 2 , 3 \\displaystyle t=0,1,2,3 t=0,1,2,3,而频率分别取 w = 2 π , 2 π 4 , 2 ∗ 2 π 4 , 3 ∗ 2 π 4 \\displaystyle w=2\\pi ,\\frac2\\pi 4 ,2*\\frac2\\pi 4 ,3*\\frac2\\pi 4 w=2π,42π,2∗42π,3∗42π来计算他们与 sin ( w t ) \\displaystyle \\sin( wt) sin(wt)和 cos ( w t ) \\displaystyle \\cos( wt) cos(wt)的相似度,即:
F s i n ( w ) = ∑ t = 0 , 1 , 2 , 3 f ( t ) sin ( w t ) F c o s ( w ) = ∑ t = 0 , 1 , 2 , 3 f ( t ) cos ( w t ) F_sin( w) =\\sum _t=0,1,2,3 f( t)\\sin( wt)\\\\ F_cos( w) =\\sum _t=0,1,2,3 f( t)\\cos( wt) Fsin(w)=t=0,1,2,3∑f(t)sin(wt)Fcos(w)=t=0,1,2,3∑f(t)cos(wt)
写成欧拉的形式就是
F ( w ) = ∑ t = 0 , 1 , 2 , 3 f ( t ) e i w t F( w) =\\sum _t=0,1,2,3 f( t) e^iwt F(w)=t=0,1,2,3∑f(t)eiwt
快速离散傅里叶变换(FFT)
理解快速离散傅里叶变换的关键在于,意识到:
F ( 2 π ) = ∑ t = 0 , 1 , 2 , 3 f ( t ) e i 2 π t = f ( t 1 ) + f ( t 2 ) + f ( t 3 ) + f ( t 4 ) F ( 2 π 4 ) = ∑ t = 0 , 1 , 2 , 3 f ( t ) e i 2 π 4 t = f ( t 1 ) + f ( t 2 ) e i 2 π 4 + f ( t 3 ) ( e i 2 π 4 ) 2 + f ( t 4 ) ( e i 2 π 4 ) 3 F ( 2 ∗ 2 π 4 ) = ∑ t = 0 , 1 , 2 , 3 f ( t ) ( e i 2 π 4 t ) 2 = f ( t 1 ) + f ( t 2 ) ( e i 2 π 4 ) 2 + f ( t 3 ) ( e i 2 π 4 ) 4 + f ( t 4 ) ( e i 2 π 4 ) 6 F ( 3 ∗ 2 π 4 ) = ∑ t = 0 , 1 , 2 , 3 f ( t ) ( e i 2 π 4 t ) 3 = f ( t 1 ) + f ( t 2 ) ( e i 2 π 4 ) 3 + f ( t 3 ) ( e i 2 π 4 ) 6 + f ( t 4 ) ( e i 2 π 4 ) 12 F( 2\\pi ) =\\sum _t=0,1,2,3 f( t) e^i2\\pi t =f( t_1) +f( t_2) +f( t_3) +f( t_4)\\\\ F\\left(\\frac2\\pi 4\\right) =\\sum _t=0,1,2,3 f( t) e^i\\frac2\\pi 4 t =f( t_1) +f( t_2) e^i\\frac2\\pi 4 +f( t_3)\\left( e^i\\frac2\\pi 4\\right)^2 +f( t_4)\\left( e^i\\frac2\\pi 4\\right)^3\\\\ F\\left( 2*\\frac2\\pi 4\\right) =\\sum _t=0,1,2,3 f( t)\\left( e^i\\frac2\\pi 4 t\\right)^2 =f( t_1) +f( t_2)\\left( e^i\\frac2\\pi 4\\right)^2 +f( t_3)\\left( e^i\\frac2\\pi 4\\right)^4 +f( t_4)\\left( e^i\\frac2\\pi 4\\right)^6\\\\ F\\left( 3*\\frac2\\pi 4\\right) =\\sum _t=0,1,2,3 f( t)\\left( e^i\\frac2\\pi 4 t\\right)^3 =f( t_1) +f( t_2)\\left( e^i\\frac2\\pi 4\\right)^3 +f( t_3)\\left( e^i\\frac2\\pi 4\\right)^6 +f( t_4)\\left( e^i\\frac2\\pi 4\\right)^12 F(2π)=t=0,1,2,3∑f(t)ei2πt=f(t1)+f(t2)+f(t3)+f(t4)F(42π)=t=0,1,2,3∑f(t)ei计算机视觉 图像的傅里叶变换