论文导读Selecting Data Augmentation for Simulating Interventions

Posted 2022-12-03 ViviranZ

这一篇从数据增强的角度切入因果AI，主要处理的也是OOD generalization的问题

目录

【摘要】

【Introduction】

【Method】

2.2. 基于因果关系的领域泛化和数据扩充

2.3. 模拟的干预措施

2.4. 为域泛化选择数据扩充

---

【摘要】

用纯粹的观察数据和经验风险最小化原则(Vapnik, 1992)训练的机器学习模型可能无法推广到看不见的领域。在这篇论文中，我们关注的是由于观测域和实际任务标签之间的虚假关联而产生的问题。我们发现许多域泛化方法并没有明确地考虑到这种伪相关。相反，特别是在更面向应用的研究领域，如医学成像或机器人，基于启发式的数据增强技术被用于学习领域不变特征。为了弥合理论和实践之间的差距，我们对领域泛化问题发展了一个因果观点。我们认为因果概念可以通过描述它们如何削弱观察域和任务标签之间的虚假相关性来解释数据增强的成功。我们证明了数据增强可以作为模拟介入数据的工具。我们使用这些理论见解来推导出一个简单的算法，该算法能够选择数据增强技术，从而实现更好的领域泛化。

【Introduction】

尽管在深度学习的推动下，机器学习最近取得了进步，但Azulay和Weiss(2019)等研究表明，深度学习方法可能无法推广到训练分布之外的输入。然而，在医疗成像、机器人和自动驾驶汽车等安全关键领域，机器学习模型对环境变化的鲁棒性至关重要。如果没有概括的能力，机器学习模型就不能安全地部署在现实世界中。

在域泛化领域，人们试图找到一种跨不同环境(称为域)进行泛化的表示，每个环境的输入具有不同的移位。当域中的更改与实际任务标签中的更改伪关联时，这个问题尤其具有挑战性。例如，当数据收集过程有偏差时就会发生这种情况。Arjovsky等人举了一个例子(2019):如果我们考虑奶牛和骆驼在其自然栖息地的图像数据集，那么动物类型和图像中的景观之间存在很强的相关性，例如，一只站在沙漠中的骆驼。如果我们现在训练一个机器学习模型来预测给定图像中的动物，该模型很容易利用动物类型和景观类型之间的虚假相关性。因此，该模型可能无法识别站在绿色牧场上的骆驼或站在沙漠中的奶牛。

近年来，一个大型的方法语料库被设计用来学习跨领域泛化的表示。虽然所提出的方法能够在各种领域泛化基准上取得良好的结果，但大多数方法都缺乏理论基础。在最坏的情况下，这些方法强制执行错误类型的不变性，如附录A.6.1所示。有趣的是，我们发现，特别是在更多的应用领域，如医学成像和机器人，研究人员已经找到了一种实用的方法来处理领域和实际任务之间的虚假相关性。数据增强结合经验风险最小化(ERM) (Vapnik, 1992)被用来加强机器学习模型在领域变化方面的不变性。因此，利用先验知识来指导选择合适的数据增强方法。在附录a .7.1中，我们详细总结了两个成功的数据应用。

然而，数据增强的成功往往被描述为“人为扩展标记训练数据集”(Li, 2020)和“减少过拟合”(Krizhevsky等人，2012)等模糊的术语。在本文中，我们提出了领域泛化背景下的数据增强的因果视角，并以以下方式对该领域做出了贡献:

1.首先，我们引入了干预增强方差（intervention augmentation equivariance ）的概念，它形式化了数据增强和领域特征上的干预之间的关系。我们表明，如果干预-增强等方差成立，我们可以使用数据增强来成功地模拟仅使用观测数据的干预。

2.其次，我们推导出一个简单的算法，该算法能够从给定的转换列表中选择数据增强技术。我们将我们的方法与各种领域泛化方法在三个领域泛化基准上进行比较。我们证明了我们能够始终优于所有其他方法。

【Method】

2.1 Domain generalization

我们首先按照Muandet等人(2013)中使用的符号将域泛化问题形式化。我们假设在训练过程中，我们从N个不同的域访问样本S，其中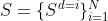。每个域的n_i个样本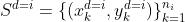包含在训练集中。训练数据被表示为从p(x, y, d)观测分布中采样的元组(x, y, d)。域泛化的目标是开发能够很好地泛化到不可见域的机器学习方法。为了测试机器学习模型的泛化能力，我们使用样本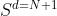，来自一个之前不可见的测试域d=N+1。

在本文中，我们对观察域d和目标y在训练数据集中虚假相关的一般情况感兴趣，即，我们可能有p(y|d = i) != p(y|d = j)， i, j∈1，…N。由于d和y之间的相关性被假设为虚假的，它不一定对测试域d = N + 1成立。

2.2. 基于因果关系的领域泛化和数据扩充

对于不熟悉因果关系概念的读者，可以在附录a .5中简单介绍全文中使用的因果概念。如需深入介绍，请参阅Pearl(2009)或Peters等人(2017)。

首先，我们引入了一个结构因果模型(SCM)，以描述我们认为在许多情况下反映了域泛化问题的潜在因果结构。SCM如图1(右)所示，其中c是一个隐藏的混杂因素(和一个外生变量)，d是域，(d就是我们想要去除的confounder，)y是目标，hd高级特征，如颜色和方向，由d引起，hy高级特征，如形状和纹理，由y引起，x是输入。为了清晰起见，我们省略了噪声变量。对应的有向无环图(DAG)如图1(左)所示，其中灰色节点表示变量被观察到，白色节点对应潜在(未观察到)变量。提出的DAG与Subbaswamy & Saria(2019)和Castro等人(2019)构建的DAG类似。在图1中，节点c是一个隐藏的混杂器。隐藏的混杂因素c打开一条后门路径(非因果路径)d←−c−→y (Pearl, 2009)。这条路径允许d通过后门进入y。

因此，定义域d和目标y一般不再独立，p(y, d) ！= p(y)p(d)。由于高级特征hd是d的子特征，它们也与y虚假相关，即hd成为y的预测。我们现在假设我们使用ERM (Vapnik, 1992)和图1中DAG产生的观察数据来训练机器学习模型。我们的任务是从x中预测y，这本身是反因果的。由于d和y是相关的，所以机器学习模型很可能会依赖于所有的高级特征hd和hy来预测y，此外，我们假设d和y的相关是虚假的。因此，在一般情况下不会保持，在干预下会打破。因此，依赖于由d引起的高级特征hd的机器学习模型很可能无法推广到不可见的领域。回到我们对图像中的动物进行分类的介绍性例子，隐藏的混杂器可以用来模拟这样一个事实:动物的类型和图像中的景观有一个共同的原因。例如，混淆器可以是某张照片拍摄的国家，例如，在瑞士，我们更有可能看到一头奶牛站在绿色的牧场上，而不是骆驼或沙漠。

2.3. 模拟的干预措施

处理d和y之间虚假相关的一种可能的方法是对d执行干预。这样的干预将使d和y独立，即p(y|do(d)) = p(y)。在图2(左)中，我们看到与图1相同的DAG，但在我们干预d之后。我们发现在图2(左)中，没有更多的箭头连接隐藏的混淆器c和域d。后门路径d←−c−→y已经消失。在动物和景观的例子中，为了干预景观，我们必须把一头牛搬到沙漠中。很明显，这些干预必须发生在现实世界中，而不是对已经收集到的观察数据进行操作。在大多数领域泛化问题中，用特定的干预措施来收集新数据是不可行的。

在图2(中间)中，我们展示了解决变量d和y相关问题的第二种方法。理论上，我们可以对所有高级特征hd进行干预，即do(hd)，因为d只通过hd间接影响x，在我们的例子中，hd可以代表景观的颜色和纹理。同样，在现实世界的数据收集过程中需要进行这样的干预，例如，将沙子移到牧场。

然而，我们认为在某些情况下，我们可以利用数据增强结合观测数据来模拟介入分布p(x, y|do(hd))的数据。例如，我们可以随机打乱动物图像中的颜色。这种类型的增强在hd上模拟了一种噪声干预，即do(h_d = ξ)，其中ξ从噪声分布N_ξ中采样(Peters等人，2016)。

理论上，我们可以通过将h_d设置为固定值来干预h_d，而不是执行噪声干预。然而，为了使用数据增强来模拟这种干涉分布的数据，我们需要观察h_d，而我们认为一般无法观测h_d。在附录a .7.1中，我们描述了现有的数据增强方法，在将所有样本的h_d设置为固定值之前，试图推断每个样本x的h_d，但这些增强似乎比随机抽样增强效果更差。

通过只增加由d引起的高级特征h_d，我们保证目标y和特征hy不变。数据增强后，(, y)应该与介入分布p(x, y|do(h_d))中的样本非常相似。在图2(右)中，我们看到我们只需要DAG的观察数据，不需要任何干预。虽然每个增强样本单独可以被视为反事实，但我们认为，通过从每个x生成大量的增强样本xaug，我们有效地边缘化了反事实分布。我们认为，对于正确选择的数据增强，我们无法区分图2中三种模型中任何一种生成的数据。

如果我们选择数据增强 = aug(x)，作为应用于观察数据x的转换aug(·)，以模拟d对高阶特征hd的干预，我们需要对数据的因果生成过程做出假设。正式地说，我们要求将数据x扩展为 = aug(x) 和在生成数据之前使用干预do(hd)的操作是交换的（Formally, we require that augmenting the data x to xaug = aug(x) commutes with an intervention do(hd) prior to the data generation.）。我们称之为干预增强方差（intervention-augmentation equivariance）。更详细地说，假设我们从方程式1中得到因果过程:。然后通过aug(·)增加x:

(2)

如果对于X∈X上的每个考虑的随机数据增强变换aug(·)，我们在Hd∈Hd上有相应的噪声干预do(·)，则我们可以说因果过程是干预-增强的等变(ntervention-augmentation equivarian)，例如:

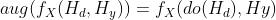。(3)

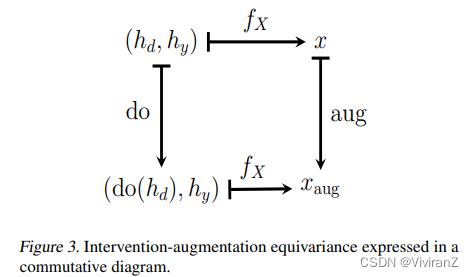
干涉-增强等方差在图3中用交换图表示。我们认为我们首先需要通过 对真正的因果过程做出强有力的假设识别由d引起的高层次特征hd。其次，我们必须选择数据增强aug(x)使得在因果过程fX(hd, hy)下与相应的干预do(hd)可交换。干涉-增强方差的特殊情况出现在G等变图fX的经典情况(in the classical case of an G-equivariant map fX)中，其中G可以是任何(半)群。为此，我们需要G作用于Hy, Hd, X空间，我们需要确保G作用于Hy空间。因此，任何元素g∈G都可以将元素X∈X转换为g·X∈X，我们将其解释为数据增强，如第4节所示。元素g∈G也将hd∈hd转化为g·hd∈hd，我们认为这是一种特殊的介入类型。此外，我们假设hy∈Hy对于所有g∈G都保持固定g·hy = hy，因此我们放入:

，(4)

，(5)

其中，我们假设元素g∈G是从G上的某个分布p(g)中随机抽样的。在这种情况下，任何G-等变的图fX都会自动地保持干涉-增强等变，如下所示:

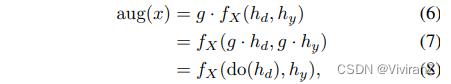
 一个干涉-增强等方差的线性例子可以在附录中找到。

一般来说，我们发现大多数经常使用的数据增强都可以表示为简单的群作用（group actions）。例如，对输入图像x进行随机旋转，可以理解为对二维旋转组SO(2)中的元素g进行随机采样，并将其应用在二维像素网格上。随机改变图像x的色调对应于从二维旋转组SO(2)中随机采样并应用元素g，因为色调可以表示为颜色空间中的一个角度。对图像x的颜色通道应用随机排列，在三个独立颜色通道的情况下，相当于对排列组S3中的元素g进行随机抽样并应用。

2.4. 为域泛化选择数据扩充

Selecting data augmentations for domain generalization

在图2(中间)中，我们可以看到如果我们成功地使用数据增强在hd上模拟干预，那么从d到hd的箭头就会消失。基于这一理论见解，我们提出了一种算法，该算法能够选择能够改善领域泛化的数据增强技术，而不是手动选择它们。下面我们将把这种算法称为选择数据增强(Select Data Augmentation, SDA)。与Cubuk等人(2019)类似，我们从一系列数据增强技术开始，包括:“亮度”、“对比度”、“饱和度”、“色调”、“旋转”、“平移”、“缩放”、“剪切”、“垂直翻转”和“水平翻转”。由于这些转换不相互影响，因此可以分别对它们进行测试。每个增强的超参数可以在附录中找到。本文提出的SDA算法包括三个步骤:

1.我们将训练域中的所有样本分成一个训练和验证集。

2. 我们训练分类器来从输入x预测域d。在训练过程中，我们对训练集的样本应用列表中的第一个数据增强。训练后将域精度保存在验证集中。我们对列表中的所有数据扩展重复此步骤。

3.我们选择了五个种子上平均域精度最低的数据增强。如果多个数据增强在所选数据的标准误差范围内，它们也被选中，即增强之间没有统计学上的显著差异。

直观上，SDA会选择破坏x中d信息的数据增强技术。从因果关系的角度来看，这相当于削弱了从d到h_d的箭头。在附录A.1.1中，我们进行了一项消融研究，表明如果列表中包含具有不同超参数的相同增广，SDA也可以可靠地选择最合适的数据增广。

不过也有一个警告。在整个章节中，我们假设我们成功地增强了所有由d引起的高级特征hd。在真实的应用中，我们通常没有方法来验证这个假设，也就是说，我们可能只增强了hd的一个子集。此外，我们甚至可能增加由目标节点y引起的高级特征hy。尽管如此，我们认为，在某些情况下，我们仍然获得更好的泛化性能，而不是没有数据增强提高训练的机器学习模型。这种情况可能发生在削弱hd对y的伪混淆影响比对y破坏的特征的数据增强恢复更多y的反因果信号的情况下。我们将在第4节对这一假设进行实证评估

3 Related Work

3.1. 学习数据中的对称性

Learning symmetries from data

在上一节中，我们认为为数据扩充选择正确的对称组依赖于先验知识，例如，预先选择要测试的转换列表。虽然这是我们方法的一个明显的实际限制，但就我们所知，目前还没有任何方法能够从纯粹的观测数据中学习对称性。当代方法如拉格朗日神经网络(Cranmer等人，2020年)、图神经网络(Kipf & Welling, 2017年)和群等变神经网络(Cohen & Welling, 2016年)正在强制执行先验选择对称，而不是学习它们。

3.2. 理解数据增强

Understanding data augmentation

最近，Gontijo-Lopes等人(2020)提出了两种衡量标准:亲和性和多样性（affinity and diversity）。这些措施用于量化现有数据增强方法的有效性。他们发现，亲和度和多样性得分高的增强能带来更好的泛化性能。虽然亲和性和多样性依赖于iid假设，但我们为非iid数据集提供了另一种选择。Lyle等人(2020)研究了如何使用数据增强将不变性纳入机器学习模型。他们表明，虽然数据增强可以导致更紧的PAC-Bayes界限，数据增强不保证导致不变性。在公式3中，我们形式化了在何种情况下(即干涉-增强等方差)数据增强会导致不变性。

3.3. 先进的数据增强技术

 Advanced data augmentation techniques 

Zhang et al.(2018)引入了一种名为mixup的方法，通过在两个现有的示例(xi, yi)和(xj, yj)之间线性插值来构建新的训练示例。在Gowal等人(2019)和Perez & Wang(2017)中，生成对抗网络(GAN)被用于执行所谓的“对抗混合”。GAN能够生成新的属于同一个类y但具有不同风格的训练示例。此外，Perez和Wang(2017)提出了一种名为“神经增强”的新方法，他们训练模型的第一部分，从具有相同类y的两个训练示例生成增强图像。

3.4. 因果关系

Peters等人(2016)提出了一种不变因果预测(ICP)的方法。它建立在给定不同的实验设置、因果特征是稳定的这个假设上。给定完整的因果特征集，目标变量y的条件分布在干预下(例如域的改变)必须保持不变。然而，依靠非因果特征的机器学习模型做出的预测在干预下通常是不稳定的。最近，Arjovsky等人(2019)提出了一个名为“不变风险最小化”(IRM)的框架，该框架与ICP有着相同的目标。在IRM中，一种结合了ERM术语的软惩罚被用来平衡学习机器学习模型的不变性和预测能力。与ICP相比，IRM可以用于非结构化数据的任务，例如图像。然而，虽然两种方法(ICP和IRM)试图学习y的父特征，我们认为，对于大多数域泛化问题，从x预测y的任务是反因果的。因此，我们感兴趣的是只增加由d引起的特征，即d的后代，并假设剩下的特征是由y引起的。在Arjovsky等人(2019)中，他们认为导致x的真实标签(部分真实因果机制)和人类标签产生的注释之间存在差异。学习这种“标签函数”将导致良好的泛化表现，即使它可能依赖于反因果或非因果的模式。在这种情况下，IRM目标变得无效。

Heinze-Deml & Meinshausen(2019)引入了条件方差正则化(Conditional variance Regularization, CoRe)。CoRe使用分组观察(例如，具有相同的类y但不同风格的训练样本)来学习不变表示。样本是通过一个额外的ID变量分组的，这个ID变量不同于标签y。我们发现在大多数情况下很难获得一个额外的ID变量，例如第4节的数据集中没有一个数据集具有这样的变量。如果不存在这样的ID变量，CoRe可以使用原始图像和增强图像对学习不变表示。

当我们关注图1中的DAG时，Bareinboim & Pearl(2016)和Mooij等人(2019)已经开发了跨领域相关数据生成过程的通用图形表示。如果观察到混淆器c，可以使用找到稳定特征集的方法，如RojasCarulla等人(2018)和Magliacane等人(2018)。此外，Subbaswamy等人(2019)表明，可以根据观测数据拟合干预分布，而不是在某些情况下进行干预。然而，成像数据提出了一个挑战，现有的基于原因的方法不具备处理，从而激励使用数据增强。

4. 实验

我们在四个数据集上评估数据增强与经验风险最小化(ERM)相结合的性能。第一个是合成数据集，其他三个是域泛化基准图像数据集(旋转的MNIST、彩色的MNIST和PACS)，其中域d和目标y是混淆的。利用合成数据集研究了域引起的高级特征和标签引起的高级特征增强时数据增强对模型性能的影响。对于基准图像数据集，我们首先使用SDA来选择最佳的数据增强技术。第一步的结果可以在附录中的表5中找到。然后，我们利用所选的数据增强，利用ERM训练各自的模型。最后，我们进行了消融研究，将所有数据增强应用于所有三个图像数据集，而不是选定的图像数据集。

Code to replicate all experiments can be found under  https://github.com/AMLab-Amsterdam/ DataAugmentationInterventions.

4.1 合成数据集

 对于第一个实验，我们在图4(右)中模拟了线性高斯SCM的数据，对应的DAG在图4(左)中可以看到。

 

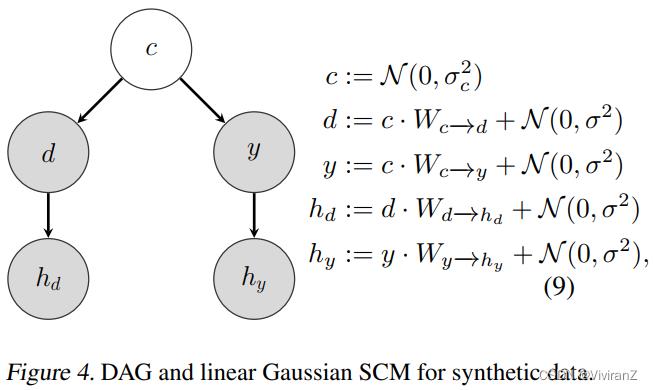
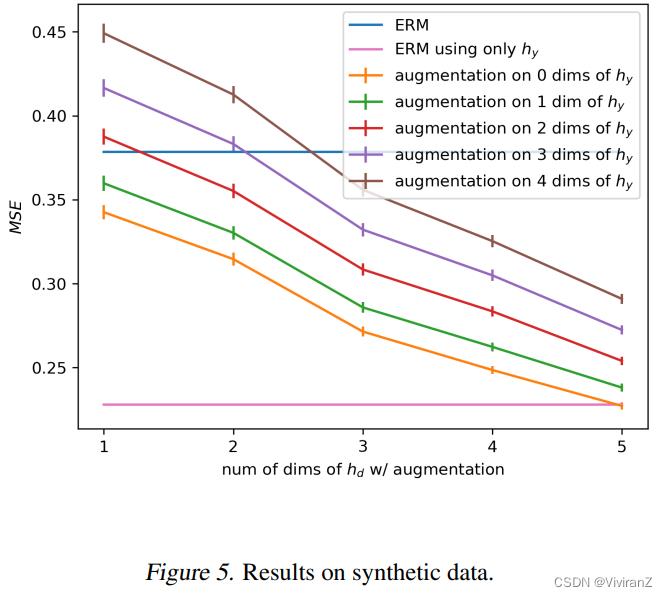
 我们选择c d y hd和hy作为五维向量。此外，我们从N (0, I)开始采样W_[c→d, W_c→y, W_d-→hd和W_y→hy的方阵元素，在所有的实验中σ_c =I和σ = 0.1·I。我们的任务是从x回归，其中x = [hd, hy]是一个10维特征向量。在训练过程中，使用图4(左)中的DAG生成数据，其中由于混淆器c，特征hd和y是虚假相关的。测试时设置d:= N (0, I)，保持W_c→d, W_c→y, W_d→hd和W_y→hy与训练时相同。因此，特征hd和y不再相关。一个依赖于hd特征的模型将不能很好地推广到测试数据。在所有的实验中，我们使用线性回归来最小化经验风险。我们选择添加从均匀分布U[−10,10]采样的噪声作为我们的数据增强技术。我们改变增加的hd和hy的维数。每个实验重复50次，在图5中我们绘制了均方误差(MSE)的均值和标准误差。

在图5中，我们看到仅使用hy(粉色线)特性的ERM实现了最低的MSE。接下来，我们对hd的1、2、3、4和5个维度进行数据增强，同时保持hy(橙色线)不变。我们发现，如果将数据增广应用于hd的所有五个维度，我们可以用特征hy匹配ERM的MSE。在这种情况下，我们满足方程3中的条件。此外，我们不出所料地发现，使用 应用于特征hy的数据增强 训练的模型的MSE增加(绿色，红色，紫色和棕色线)。然而，我们可以看到，只要我们将数据增强应用到至少三个hd维度上，使用hd和hy(蓝线)所有特征，得到的MSE低于ERM（as long as we apply data augmentation to at least three dimensions of hd the resulting MSE is lower than ERM using all features hd and hy (blue line).）。也许这个实验最令人惊讶的结果是，在存在的条件下，对d引起的特征和y引起的特征进行数据增强会比使用所有特征的ERM产生更好的泛化性能。（there exist conditions under which applying data augmentation to features caused by d and features caused by y will result in better generalization performance compared to ERM using all features）

4.2. 旋转MNIST

我们根据Li等人(2018)构建了旋转的MNIST数据集。这个数据集由四个不同的域d和十个不同的类别y，每个域对应不同的旋转角度:d =0◦，30◦，60◦，90◦。我们首先从MNIST训练数据集中随机选择图像x的子集，然后对该子集的每个图像应用旋转。对于下一个域，我们随机选择一个新的子集。为了保证p(y)在各域之间的方差，每个数字类y的训练示例数从均匀分布U[80,160]中随机选取。

对于每个实验，选择三个领域进行训练和一个领域进行测试。对于测试域，对MNIST测试集的10000个示例应用相应的旋转。在表2中，我们将结合ERM的数据增强与ERM、域对抗神经网络(DANN) (Ganin等人，2016)和条件域对抗神经网络(CDANN) (Li等人，2018)进行了比较。所有方法都使用LeNet (LeCun et al.， 1998)型架构，每个实验重复10次。首先，我们使用SDA来寻找最佳的数据增强技术，其中我们对域分类器使用相同的LeNet模型和训练过程，只从训练域中获取样本。在所有四种情况下，领域精度最低的数据增强是“旋转”，我们在其中留下一个领域进行测试。此外，我们进行了消融研究，结果表明SDA可靠地选择了最合适的超参数，结果见附录中的表4。其次，我们应用0◦和359◦之间的随机旋转图像x在培训期间，由DA表示。如果我们假设hd等于给定图像x中MNIST数字的旋转角度，对x施加随机旋转就等于对hd进行噪声干预，见公式3。如第2节所述，对x进行随机旋转可以理解为从二维旋转组SO(2)中随机抽样元素g。注意元素g∈SO(2)对hy的作用很简单:旋转不会改变数字的形状。结果是d和y是独立的训练数据集。在表2中，我们看到DA的结果对于所有四个测试域都是相似的。此外，我们发现DA优于ERM、DANN和CDANN，其中CDANN是专门为d和y虚假相关的情况设计的。 

 

 4.3. 彩色MNIST

在Arjovsky等人(2019)之后，我们创建了一个版本的MNIST数据集，其中每个数字的颜色与一个二进制标签y虚假相关。我们构建了两个训练域和一个测试域，其中原始MNIST类' 0 '到' 4 '的数字被标记为y = 0，类' 5 '到' 9 '的数字被标记为y = 1。随后，对于25%的数字，我们翻转标签y。现在我们将标记为y = 0的数字涂上红色，标记为y = 1的数字涂上绿色。最后，我们在第一个训练域和第二个训练域分别以0.2和0.1的概率翻转一个数字的颜色。在测试域的情况下，数字的颜色翻转的概率为0.9。根据设计，每个数字(' 0 '到' 9 ')的原始MNIST类是新标签y的直接原因，而每个数字的颜色是新标签y的后代。

彩色MNIST的DAG，如图6所示，与图1中的DAG稍有偏差，尽管如此，第2节中的推理仍然是有效的。在表1中，我们看到，虽然ERM在训练领域表现良好，但它未能推广到测试领域，因为它是使用颜色信息来预测y。相反，IRM (Arjovsky等人，2019)和REx (Krueger等人，2020)推广到测试领域很好。同样，我们使用SDA来找到适当的数据增强。对于域分类器，我们使用与Arjovsky等人(2019)相同的MLP和训练程序。我们想要强调的是，SDA只依赖于来自两个训练域的样本，而IRM和REx的超参数则对来自测试域的样本进行了调整，如Krueger等人(2020)所述。对于有色MNIST数据集，选择的数据增强是“hue”和“translate”，用DA表示。如第2节所述，对x的色调值应用随机排列，相当于从排列群SO(2)中随机抽样并应用元素g。我们认为元素g不会改变hy:包含关于每个数字形状的信息的高级特征。在我们的实验中，我们使用与Arjovsky等人(2019)描述的相同的网络架构和训练程序。每个实验重复10次。我们发现DA可以成功地削弱d域对y的杂散影响，见表1

4.4。PACS

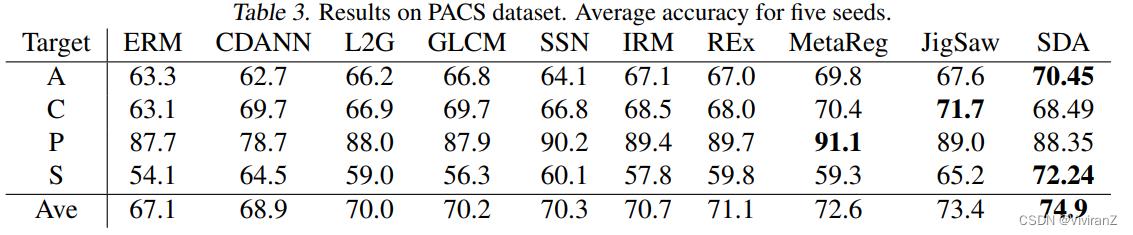
PACS数据集(Li et al.， 2017a)被引入为具有较大域偏移特征的域泛化方法的强基准数据集。f每个域的镜像数量分别为1670、2048、2344、3929。有七个类:y =[狗，大象，长颈鹿，吉他，马，房子，人]。我们微调alexnet模型(Krizhevsky等人，2012)，该模型在ImageNet上进行了预训练，使用ERM结合数据增强。在接下来的实验中，我们使用SDA来选择数据增强。对于域分类器，我们如上所述对alexnet模型进行微调。此外，我们使用交叉验证过程，其中我们去掉一个域，使用三个域进行培训。SDA确定了四种有用的数据增强技术:“亮度”、“对比度”、“饱和度”和“色调”。在组合这四种增强通常被称为颜色抖动或颜色扰动。通过随机应用颜色扰动，我们弱化了hd对y的伪混淆影响，如第2节所述。在表3中，我们将DA与各种域泛化方法进行比较:CDANN (Li等人，2018年)、L2G (Li等人，2017b)、GLCM (Wang等人，2018年)、SSN (Mancini等人，2018年)、IRM (Arjovsky等人，2019年)、REx (Krueger等人，2020年)、MetaReg (Balaji等人，2018年)、JigSaw (Carlucci等人，2019年)，其中所有方法都使用相同的预训练alexnet模型。每个实验重复5次，报告平均准确率。我们发现DA的平均准确率最高。与ERM相比，DA在“艺术绘画”和“素描”两个测试领域的成绩提高最大。例如，域“草图”由白色背景上的七个对象类的黑色草图组成，参见图7。由于对象的颜色与类不相关，依赖于颜色特征的模型将很难推广到“草图”领域。然而，通过随机改变训练域中(“艺术绘画”、“卡通”、“照片”)图像的颜色，我们发现DA能够更好地概括。

消融研究:使用所有数据增强技术我们使用附录中列出的所有数据增强技术，在旋转MNIST、有色MNIST和PACS上重复之前的实验。我们比较了使用所有数据增强技术训练的分类器和使用SDA训练的分类器的准确性。我们发现，同时使用所有数据增强技术会导致所有三个数据集的性能显著下降:旋转MNIST的性能下降25.4%，有色MNIST的性能下降8.7%，PACS的性能下降16.1%。我们观察到数据集和数据增强技术的组合本身会导致性能的急剧下降，例如PACS数据集和随机旋转。我们认为，没有随机旋转训练的模型利用了一个事实，例如，动物或人的方向通常是直立的。这个例子表明，我们不能简单地将数据增强描述为“标签保存转换”，因为旋转后的动物或人仍然会有相同的标签。

5. 结论

这篇论文中，从因果的角度研究了领域泛化中数据增强的有效性。通过使用SCM，我们解决了区域泛化的一个核心问题:区域变量d和目标变量y的虚假相关性。虽然在理论上，我们可以对区域变量d进行干预，但这种解决方案是不切实际的，因为我们假设我们只能获得观测数据。然而，我们表明，数据增强可以作为模拟领域变量d及其子变量干预的替代工具。因此，先验知识可以用来选择只作用于目标变量y的非后代的数据增强技术。此外，我们表明，随机应用数据增强可以理解为从常见对称群中随机抽样元素。此外，我们提出了一个简单的算法来从给定的转换列表中选择合适的增广技术。我们使用一个域分类器来衡量每个增强在多大程度上削弱了领域d和由d引起的hd高级特征之间的因果联系。我们在四个不同的数据集上评估了这种方法，能够表明经验风险最小化结合准确选择的数据增强产生良好的泛化性能。本文的分析可进一步应用于利用干涉增强等方差设计干涉数据增强来模拟领域泛化方法的干涉数据集

比较吸引我的点在于：

1.用图1的因果图+共因来解释spurious relation的产生

2.用切断d和hd的方式（do-calculus）分离hd的影响

3.用随机域分类器实现切断※※