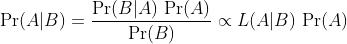论文导读Learning Bayesian Networks: The Combination of Knowledge and Statistical Data

Posted 2022-12-06 ViviranZ

这一篇是为了看看BIC函数的，快快过

【摘要】

我们描述了一种从先验知识和统计数据的组合中学习贝叶斯网络的贝叶斯方法。首先，我们开发了一种方法来评估学习所需的信息性先验。我们的方法来自于以前提出的一系列假设，如似然等价的假设，即数据不应有助于区分代表相同条件独立性断言的网络结构。我们表明，当与以前所做的假设相结合时，意味着用户对网络参数的先验可以在一个单一的贝叶斯网络中编码，以备下一个案例的出现--一个先验网络和对该网络的单一置信测量。（We show that likelihood equivalence when combined with previously made assumptions implies that the nser's priors for network parameters can be encoded in a single Bayesian network for the next case to be seen--a prior network and a single measure of confidence for that network.）第二，使用这些先验，我们展示了如何计算给定数据的网络结构的相对后验概率。第三，我们描述了用于识别具有高后验概率的网络结构的搜索方法。我们描述了在每个节点最多拥有k=1个父节点的特殊情况下寻找最高得分网络结构的多项式算法。对于一般情况（k>1），即Np-hard，我们回顾了启发式搜索算法，包括局部搜索、迭代局部搜索和模拟退火。最后，我们描述了一种评估贝叶斯网络学习算法的方法，并将这种方法用于各种方法的比较。

【综述】

贝叶斯网络是一个带注释的有向图，它编码了不确定推理问题（uncertain-reasoning problem）中人们感兴趣的区别之间的概率关系（Howard & Matheson, 1981; Pearl, 1988）。这个表示正式编码了其领域的联合概率分布，但包括一个面向人类的定性结构，以促进用户和包含概率模型的系统之间的交流。我们在第2节中详细讨论该表示法。十多年来，人工智能研究人员已经使用贝叶斯网络来编码专家知识。最近，人工智能研究人员和统计学家开始研究学习贝叶斯网络的方法，包括贝叶斯方法（Cooper & Herskovits, 1991; Buntine, 1991; Spiegelhalter等人, 1993; Dawid & Lauritzen, 1993; Heckerman等人, 1994），准贝叶斯方法（Lam & Bacchus, 1993; Suzuki, 1993），以及非贝叶斯方法（Pearl & Verma, 1991; Spirtes等人, 1993）。

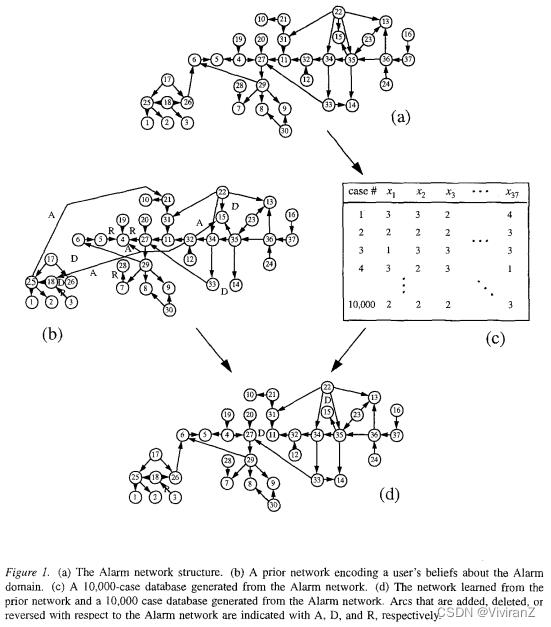
在本文中，我们专注于贝叶斯方法，它采用先验知识，并将其与数据相结合产生一个或多个贝叶斯网络。在图1展示了我们针对ICU呼吸机管理的问题的方法。使用我们的方法，用户通过构建贝叶斯网络（称为先验网络）和评估他对该网络的信心来具体化他对该问题的先验知识。图lb显示了一个假想的先验网络（概率没有显示）。此外，如图lc所示，一个案例的数据库被组装起来。数据库中的每个案例都包含了对用户先验网络中每个变量的观察--然后我们的方法利用这些信息源，学习一个（或多个）新的贝叶斯网络，如图ld所示。为了体会该方法的有效性，请注意数据库是由图la中被称为the Alarm network的贝叶斯网络生成的（Beinlich等人，1989）。比较这三种网络结构，我们看到学习到的网络结构比先验网络的结构更接近于Alarm网络的结构。实际上，我们的学习算法已经使用数据库来 "纠正 "用户的先验知识。

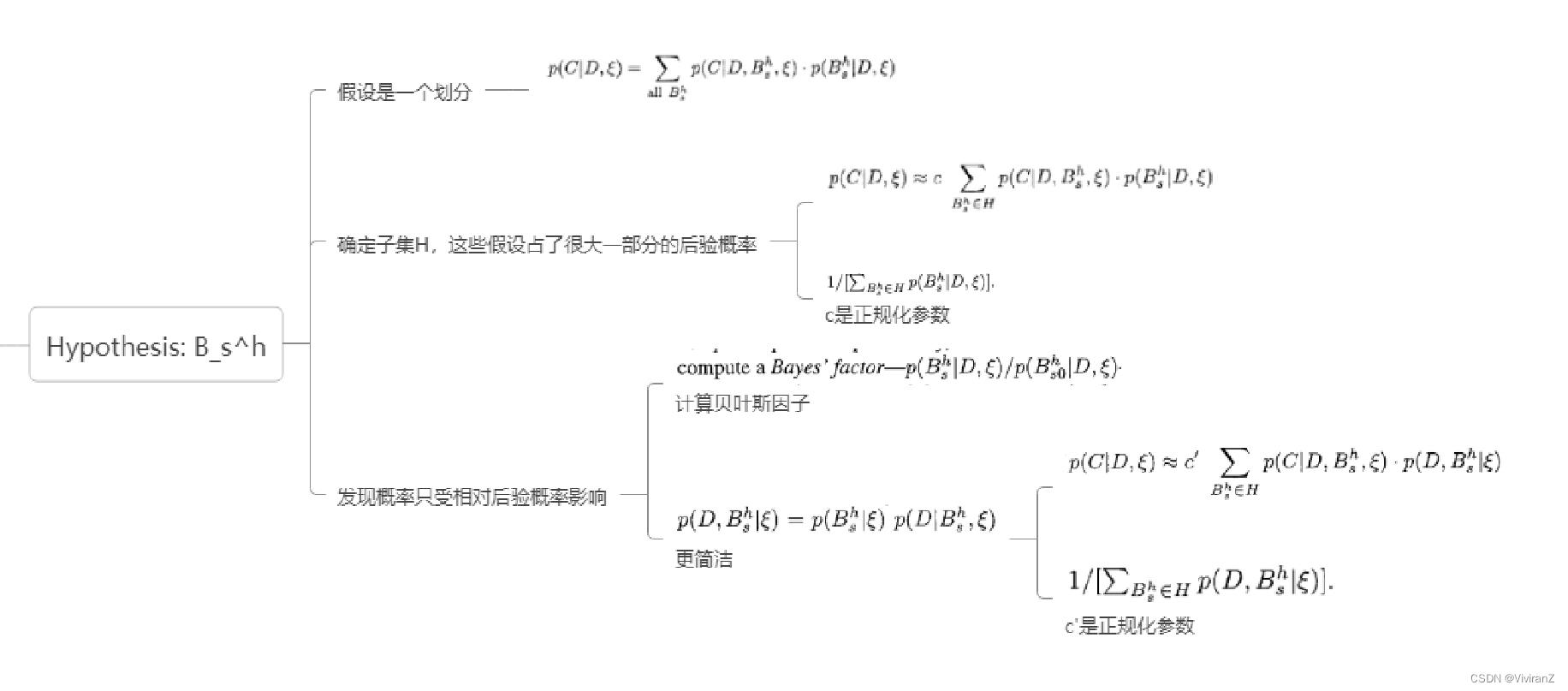
 我们的贝叶斯方法可以理解如下。假设我们有一个离散变量zl,...,zn=U的域，和一个案例C1,...,C_m=D的数据库。此外，假设我们希望在给定鉴于数据库和我们当前的信息状态\\xi的情况下确定联合分布p(C|D, \\xi)--即一个新案例C的概率分布。与其直接推理这个分布，我们想象数据是由一个我们不知道的、包含未知参数的贝叶斯网络结构B_s生成的随机样本，用B_s^h表示“数据是由网络结构B_s产生的”这个假设，并假设对应于所有可能的网络结构的假设形成一个互斥的、集体的穷举集，我们有

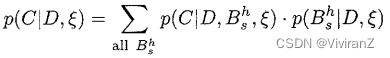
在实践中，不可能对所有可能的网络结构进行汇总。因此，我们试图确定一小部分网络结构假设的子集H，这些假设占了很大一部分的后验概率。重写前面的方程式，我们得到 

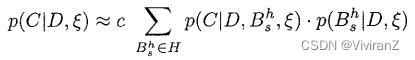
其中c是正规化参数 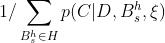，从这个关系中，我们看到只有假设的相对后验概率是重要的。因此，与其计算后验概率，即对所有结构进行求和，不如计算一个贝叶斯因子（Bayes' factor)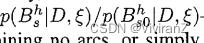，其中含s_0的概率表示一个特定的基准结构（如没有边的图），或者只是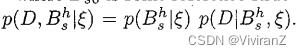，在这个情况下，有

 其中c‘是另一个正规化参数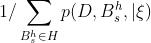

  简而言之，学习贝叶斯网络的贝叶斯方法相当于寻找具有高相对后验概率的网络结构假设。许多非贝叶斯方法使用相同的基本方法，但对结构与数据的匹配程度的使用其他优化量度。一般来说，我们把这种措施称为评分指标。我们把计算网络结构假设的相对后验概率的任何公式称为贝叶斯评分指标。

贝叶斯方法不仅是求p(C|D, \\xi)的近似值，而且是学习网络结构的方法。当IHI=1时，我们学习一个单一的网络结构——U的MAP（最大后验）结构；当IHI>1时，我们学习一个网络结构集合。正如我们在第4节所讨论的，学习网络结构是很有用的，因为我们有时可以利用结构来推断一个领域的因果关系，从而预测干预措施的效果。

在设计贝叶斯学习程序的过程中，最具挑战性的任务之一是确定一类易于评估的信息性先验，以计算方程1右侧的条款。在本文的第一部分（第3节到第6节），我们阐述了一套离散网络的假设（只包含离散变量的网络），这导致了这样一类信息性预设。我们的假设是基于Cooper和Herskovits（1991年，1992年）（下文称为CH）Spiegelhalter等人（1993年）和Dawid和Lauritzen（1993年）（下文称为SDLC）以及Buntine（1991年）的假设。这些研究者假设了参数独立性，即与贝叶斯网络中每个节点相关的参数是独立的；参数模块化，即如果一个节点在两个不同的网络中具有相同的父本，那么与该节点相关的参数的概率密度函数在两个网络中是相同的；以及迪利克雷假设，即所有网络参数具有迪利克雷分布。狄利克雷分布(Dirichlet Distribution) - 知乎狄利克雷过程概述什么时候需要用狄利克雷分布？问题背景问题特点可行方法什么是狄利克雷分布？数学形式及解释实例Chinese Restaurant Process狄利克雷过程（Dirichlet Process, DP) 概述狄利克雷分布是一种“分布…https://zhuanlan.zhihu.com/p/78743630我们假设参数的独立性和参数的模块化，但是我们没有采用Dirichlet假设，而是引入了一个叫做似然等价的假设，即数据不应该有助于区分代表相同条件独立性断言的网络结构。（data should not help to discriminate network structures that represent the same assertions of conditional independence. ）我们认为，在学习无因贝叶斯网络时，这一属性是必要的，而在学习因果贝叶斯网络时，这一属性也是合理的。然后我们表明，当与参数独立性和几个弱条件相结合时，似然等价意味着Dirichlet假设。此外，我们还表明，似然等价以这样一种方式约束了Dirichlet分布，即它们可以从用户的先验网络（即接下来要看到的贝叶斯网络）以及反映用户对其先验网络信心的单一等价样本量中获得。

我们的结果有积极和消极两方面。在积极方面，我们表明参数独立性、参数模块化和似然等价性导致了一种简单的评估先验的方法，它要求用户只对整个领域的一个等价样本量进行评估。在消极方面，该方法有时过于简单：一个用户可能对一个领域的某一部分比另一部分有更多的知识。我们认为，参数独立性和可能性等价的假设有时过于强烈，并提出了一个放松这些假设的框架。

学习贝叶斯网络的一个更直接的任务是使用一个给定的信息性先验来计算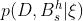（即贝叶斯的评分指标）和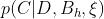。当数据库是完整的(也就是说，当没有缺失的数据时)这些条款可以以封闭的形式得出。否则，可以使用众所周知的统计学近似方法。在本文中，我们只考虑完整的数据库，并推导出这些项的闭合形式表达。其结果是一个似然等效的贝叶斯评分度量，我们称之为BDe度量。这个度量将与不使用先验网络的CH和Buntine的度量，以及不满足似然等价属性的CH和SDLC的度量进行对比。

 在本文的第二部分（第7节），我们研究了寻找高分网络的方法。这些方法可以用于许多贝叶斯和非贝叶斯的评分指标。我们描述了在每个节点最多有一个父节点的特殊情况下寻找最高分网络的多项式算法。此外，我们还描述了一般情况下的局部搜索和退火算法，众所周知，这种算法是NP困难的。

最后，在第8节和第9节中，我们描述了一种评估学习算法的方法。我们用这种方法来比较各种评分指标和搜索方法。我们注意到一些研究者（例如Dawid & Lauritzen, 1993; Madigan & Raftery, 1994）已经开发了学习无定向网络结构的方法，如（例如）Lauritzen（1982）所述。在本文中，我们专注于学习有向模型，因为我们有时可以用它们来推断因果关系，也因为大多数用户认为它们更容易解释。

【背景】

 在这一节中，我们介绍了我们的讨论所需要的符号和背景材料，包括对贝叶斯网络、可交换性、多叉取样和迪利克雷分布的描述。在第240页的附录之后，给出了一个出场符号的总结。

在整个讨论中，我们考虑一个由n个离散变量组成的域U。我们用小写字母来指代变量，用大写字母来指代变量的集合。我们写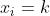表示变量xi处于状态k。当我们观察集合X中每个变量的状态时，我们把这组观察结果称为X的状态；我们写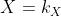作为观察结果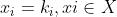的缩写。U的联合空间是U的所有状态的集合。我们用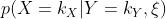表示对于一个具有当前信息状态\\xi的人来说，给定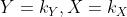的概率。 我们用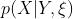表示在给定Y的所有可能的观测值的情况下，X的所有可能的观测值的概率集合。 U的联合概率分布是U的联合空间的概率分布。

域U的贝叶斯网络表示U上的联合概率分布。该表示由一组局部条件分布与一组条件独立性断言相结合，使我们能够从局部分布中构建一个全局联合概率分布。特别是，根据概率的chain rule，我们有

贝叶斯网络结构B_s编码了方程3中的条件独立性的断言。也就是说，B_s是一个有向无环图，即（1）U中的每个变量都对应于B_s中的一个节点，（2）x_i对应的节点的父节点是\\Pi_i中变量对应的节点。(在本文中，我们用x_i来指代变量和它在图中的对应节点）。一个贝叶斯网络概率集Bp是域中每个节点的局部分布p(xi|\\Pi_i, \\xi)的集合。U的贝叶斯网络是一对（B_s，B_p）。结合公式2和3，我们可以看到，任何针对U的贝叶斯网络都能唯一地决定U的联合概率分布，即  

 当一个变量只有两种状态时，我们说它是二元的。图2中显示了三个二元变量xl,x2和x3的贝叶斯网络。我们看到。因此，这个网络代表了条件独立性断言。
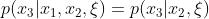可能发生的情况是，两个贝叶斯网络结构代表相同的条件独立性约束--也就是说，一个结构所编码的每个联合概率分布都可以由另一个结构编码，反之亦然。在这种情况下，这两个网络结构被认为是等价的(equivalent)（Verma & Pearl, 1990）。例如，结构x_1→x_2→x_3和x_1←x_2←x_3都表示Xl和X3在给定x2的条件下是独立的，并且是等价的，在本文的一些技术讨论中，我们将需要以下等价网络的特征，在Chickering（1995a）和附录中证明。

        Proof: 首先 满足1.2.3.的一定是equivalent的: 只需要证3.变化后的图是equivalent的：

        对于x的任何parent z，（y的parent同理），懒得分情况讨论了

        其次，equivalent的一定可以这么做：显然

贝叶斯网络的一个缺点是，网络结构取决于变量顺序。如果顺序选择不慎，产生的网络结构可能无法揭示领域中的许多条件独立性。幸运的是，在实践中，贝叶斯网络通常使用因果关系的概念来构建。宽泛地说，为给定的变量集构建贝叶斯网络，我们从原因变量到它们的直接影响画弧。例如，如果我们认为x2是x1的直接child，x3是x2的直接child，我们就会得到图2中的网络结构。"在几乎所有的情况下，以这种方式构建贝叶斯网络，会得到一个与正式定义一致的贝叶斯网络。在第4节，我们将回到这个问题上。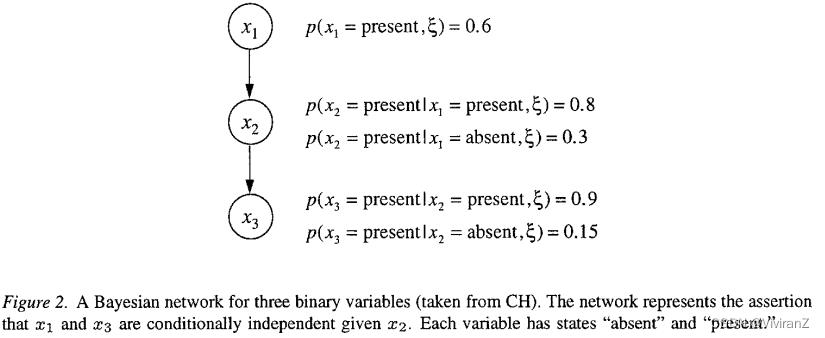

 现在，让我们考虑交换性和随机抽样。我们讨论的大部分概念可以在Good（1965）和DeGroot（1970）中找到。给定一个有r个状态的离散变量y，考虑这个变量的有限观察序列Y1, - -, Ym。我们可以把这个序列看作是单变量域U=y的数据库D。如果通过交换序列中的任何两个观测值而得到的序列具有与原始序列相同的概率，那么这个序列被称为可交换的（exchangeable）。粗略地说，一个序列是可交换的假设是一个断言，即产生数据的过程在时间上没有变化。

【比如：独立的实验-抛硬币等，但是流体的动力学状态就不是可交换的】

也就是说，参数使序列中的各个观测值有条件地独立，而任何给定的观测值处于状态k的概率只是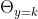。条件独立断言（等式6）可以表示为一个贝叶斯网络，如图3所示。根据强大数法则（例如DeGroot, 1970, p.203），我们可以把 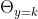看作是y=k的长期观察值的一部分，尽管还有其他解释（Howard, 1988）。还要注意，每个参数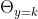都是正的（即大于零）。

满足这些条件的序列是一种特殊类型的随机样本，被称为具有参数的(r - 1)-二维多指标样本（Good，1965）。当r=2时，该序列被称为二项式样本。二项式样本的一个例子是一个图钉的重复翻转的结果。如果我们知道一个给定的图钉的 "头"（尖儿向下）的长期分数，那么每次翻转的结果都是独立、并且其概率等于这个分数。多项式样本的一个例子是一个多面体骰子的反复滚动的结果。正如我们将看到的，学习离散领域的贝叶斯网络基本上可以简化为学习具有许多面的骰子的参数问题。

由于是一组连续变量，它有一个概率密度，我们用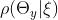表示。在本文中，我们用来表示连续变量或连续变量集的概率密度。给定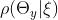，我们可以确定在下一次观察中y=k的概率。特别是，根据概率的规则，我们有

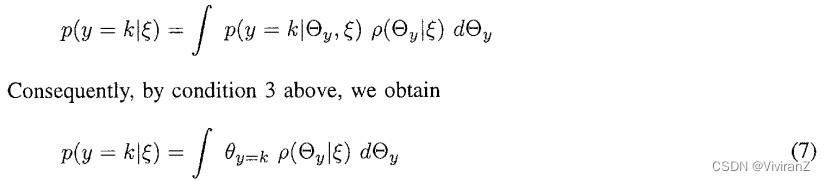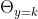 这是   相对于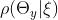的平均值或期望值，表示为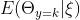。假设我们有一个的先验密度，然后观察数据库D。获得的后验密度如下。根据贝叶斯规则，我们有

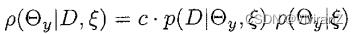
贝叶斯法则是关于随机事件A和B的条件概率和边缘概率的。

其中L(A|B)是在B发生的情况下A发生的可能性。

在贝叶斯法则中，每个名词都有约定俗成的名称：

Pr(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。

Pr(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。

Pr(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。

Pr(B)是B的先验概率或边缘概率，也作标准化常量（normalized constant）。

按这些术语，Bayes法则可表述为：

后验概率= (相似度 *先验概率)/标准化常量

也就是说，后验概率与先验概率和相似度的乘积成正比。

另外，比例Pr(B|A)/Pr(B)也有时被称作标准相似度（standardised likelihood），Bayes法则可表述为：后验概率 = 标准相似度 * 先验概率

其中c是一个归一化常数。使用方程6重写右手边的第一项，我们可以得到

其中N_k 是x = k in D发生的次数。请注意，只有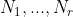这些计数对于从先验中确定后验是必要的。这些计数被说成是多项式样本的充分统计量。

此外，假设我们对两种不同的信息状态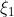和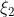评估了一个密度，发现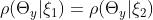。那么，对于任何多项式样本D。

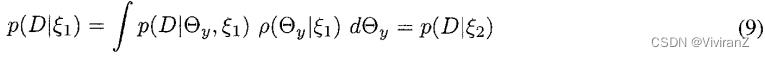
 因为根据公式6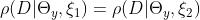，。也就是说，如果的密度是相同的，那么任何两个样本的概率都是相同的。反过来也是如此。也就是说，如果对所有数据库D来说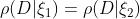，，那么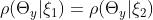。我们将在讨论似然等价时使用这一等价。
给定一个多项式样本，用户可以自由评估的任何概率密度。然而，在实践中，人们经常使用迪里切特分布，因为它有几个方便的特性。当的概率密度由以下公式给出时，参数Oy具有指数为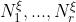的迪里切特分布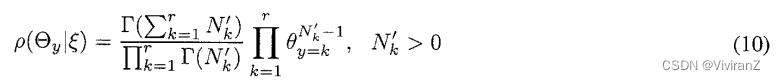 

 其中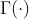是Gamma函数，它满足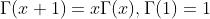。当参数具有Dirichlet分布时，我们也说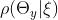是Dirichlet。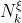大于0的要求保证了分布可以被归一化。请注意，指数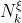是用户的信息状态的函数 bb。还要注意的是，根据方程5，的Dirichlet分布在技术上是对于给定k上的密度，（符号\\表示集差）。尽管如此，我们还是要如实写出方程10。当r=2时，Dirichlet分布也被称为β分布。 

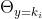 其中c是一个归一化常数。我们说Dirichlet分布在多项式取样下是封闭的，或者说Dirichlet分布是多项式取样的共轭分布族。另外，当具有Dirichlet分布时，的期望值等于下一次观察中x=ki的概率--有一个简单的表达。 

 其中。我们将在推导中利用这些特性。

Winkler（1967）对评估β分布的方法做了一个调查。这些方法包括使用有关相对密度和相对面积的问题直接评估概率密度，使用分位数评估累积分布函数，评估给定假设证据的分布的后验手段，以及以等效样本量的形式评估。这些方法可以以不同的难度被推广到非二元的情况。

在我们的工作中，我们发现一种基于方程12的方法特别有用。该方程说，我们可以通过评估下一个观察的概率分布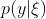和N'来评估Dirichlet分布。 这样，我们可以将方程10改写为 

 其中c是一个归一化常数。评估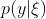是直截了当的。此外，以下两个观察结果表明了评估N'的简单方法。

其一，密度的方差表明，在新的观测条件下，的平均值预计会有多大的变化。方差越大，预期变化就越大。有时可以说，方差是用户对的平均值的信心的一种衡量。Dirichlet分布的方差由以下公式给出

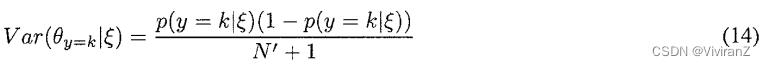
 因此，N'是对用户信心的反映。其二、假设我们最初对一个领域完全无知--也就是说，我们的分布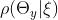是由方程10给出的，每个指数。假设我们后来看到了N‘个具有充分统计量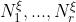的案例。那么，根据公式11，我们的先验是由公式10给出的Dirichlet分布。

因此，我们可以把N’评估为一个等效的样本量：这样的一个数字：我们想要获得我们应有的对于的信心，所需要的从完全无知开始的观察数字（:the number of observations we would have had to have seen starting from complete ignorance in order to have the same confidence in that we actually have.）这种评估方法很容易被推广到多变量领域，因此对外面的工作很有用。我们注意到，有些用户一开始发现对等价样本量的判断很困难。我们对这些用户的经验是，首先在简单的情况下使用一些其他的评估方法（如分数），并检查他们的评估所隐含的等效样本量，可以使他们对该方法更加适应。

 3. Bayesian Metrics: Previous Work

略 

 4. 因果网络、因果网络和可能性等值

略

5. The BDe Metric

结合前面的假设，似然等价的假设引入了对Dirichlet指数N'_ijk的约束。其结果是BD度量的似然等价特化，我们称之为BDe度量。在这一节中，我们将推导出这个度量。此外，我们表明，作为指数约束的consequence，用户可以为所有网络结构的参数构建一个信息丰富的先验，只需为下一个要看的案例建立一个贝叶斯网络，并评估一个相等的样本量。(In addition, we show that, as a consequence of the exponent constraints, the user may construct an informative prior for the parameters of all network structures merely by building a Bayesian network for the next case to be seen and by assessing an equivalent sample size.) 最重要的是，我们表明不需要Dirichlet假设（假设4）就可以得到BDe度量。 

也就是说，参数使序列中的各个观测值有条件地独立，而任何给定的观测值处于状态k的概率只是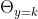。条件独立论断（等式6）可以表示为贝叶斯网络，如图3所示。根据强大数法则（例如DeGroot, 1970, p.203），我们可以把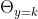看作是y=k的长期观察值的一部分，尽管还有其他解释（Howard, 1988）。还要注意，每个参数 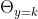都是正的（即大于零）。

 满足这些条件的序列是一种特殊类型的随机样本，被称为具有参数的(r - 1)-维多指标样本（Good，1965）。当r=2时，该序列被称为二项式样本。二项式样本的一个例子是一个图钉的重复翻转的结果。如果我们知道一个给定的图钉的 "head"（尖儿朝下）的长期分数，那么每次翻转的结果都是独立的、并且其概率等于这个“head”的分数。多项式样本的一个例子是多面体骰子反复滚动的结果。正如我们将看到的，学习离散领域的贝叶斯网络基本上可以简化为学习具有许多面的骰子的参数问题。

由于是一组连续变量，它有一个概率密度，我们用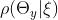表示。在本文中，我们用来表示连续变量或连续变量集的概率密度。给定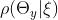，我们可以确定在下一次观察中y=k的概率。特别是，根据概率的规则，我们有

 

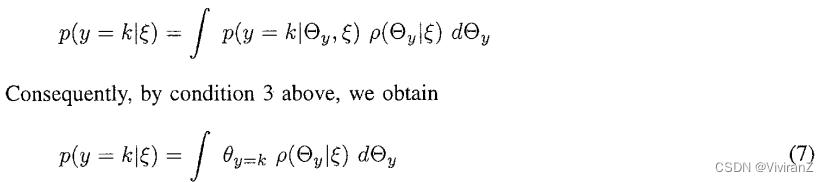
 这是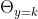相对于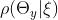的平均值或期望值，表示为。

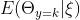假设我们有一个的先验密度，然后观察一个数据库D，我们可以得到的后验密度如下。根据贝叶斯规则，我们有

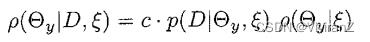
5.1. Informative Priors