论文导读‘‘Causal Protein-Signaling Networks Derived from Multiparameter Single-Cell Data

Posted 2022-04-19 ViviranZ

感谢学校买了版权！终于可以看看数据集和support material啦！

首先看看贝叶斯方法，跟原论文一样快速过一遍。

1.试剂。

2.细胞培养。

3.流式细胞仪。

4.siRNA的抑制作用

5.采用的条件。

6.数据的处理：

对数据进行了如下预处理。剔除与平均值相差超过三个标准差的数据点。然后将数据离散为三个级别（磷酸化蛋白的低、中或高水平），采用聚类方法，寻求变量间成对互信息的最小损失（5）。在化学干预的条件下，被抑制的分子被设置为1级（"低"），被激活的分子被设置为3级（"高"）。

7.模拟的西方印迹？

为了创建一个模拟的Western blot数据集，对每个条件重复以下步骤：随机选择20个细胞并取其平均值，直到所有的细胞都被平均化（每个条件产生30个模拟的Western blot数据点）。平均化将数据集的大小减少到原来的1/20，因此，另外5个含有ICAM2的条件（见上文）被用来创建模拟Western blot数据集，总共有420个数据点。对于同等大小的单细胞数据集，从14种条件中的每一种中随机选择30个细胞。这个过程重复了10次，每次都有不同的随机种子，产生10个不同的模拟西方印迹和截断的数据集。贝叶斯网络推断程序（见下文）被独立地应用于每个这样的数据集。

【可以用来处理我的ResNet数据集！！！】

8.贝叶斯网络结构推断

我们如（6，7）所述（关于该方法的评论也见Friedman（8））实现了贝叶斯网络推理。在下文中，我们将对该方法进行简短的描述，更多细节请参见在线参考资料（链接到PDF）。贝叶斯网络（9）为多变量联合概率分布提供了一个紧凑的图形表示。这种表示法由一个有向无环图组成，其节点对应于随机变量，每个随机变量代表数据集中一个生物分子的测量量。一个弧表示下游变量和上游（父）变量之间的统计依赖性。在某些情况下，这些统计依赖性可以被解释为来自母体对下游变量（分子）的因果影响（10）。例如，图1C小组b展示了干预性数据如何指导因果关系的推断。一旦有一些弧是有方向的，就会有额外的弧、其方向是 "被迫的"（就是弧由已定下来的弧决定了），否则所产生的图结构将代表数据中不成立的依赖关系。贝叶斯网络将每个变量Xi与一个概率分布联系起来，该概率分布以其在图中的父母为条件（Pai）。直观地说，父母的价值直接影响Xi的价值。图结构代表了依赖性假设，即ti'a于其在图中的父母，每个变量都独立于其非后代（条件独立）；因此，联合分布可以分解为以下形式：

 

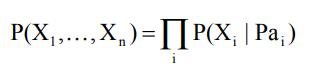
贝叶斯网络推理的目标是在可能的图中搜索，并选择一个或多个最能描述经验数据中观察到的依赖关系的图。我们采取了一种基于分数的方法：我们引入了一个有统计学动机的评分函数，根据数据对每个网络进行评估，并搜索出得分最高的网络。我们使用标准的贝叶斯评分指标（11），奖励相对简单的模型（即很少的弧），这些模型很可能产生了数据，也就是说，其基本分布接近于数据的经验分布。因为我们的数据是在直接操纵所测量的修饰生物分子量的条件下取样的（见表1B），所以我们使用了贝叶斯评分指标的改编，明确地对这些干预措施进行建模（6，7）。我们对干预措施的建模假定这些干预措施是理想的，即只直接影响一个分子，其身份是已知的。虽然所用的干预措施并不理想，但这是一个合理的第一近似值。

给定一个评分函数（上面描述的贝叶斯评分指标）和一组数据，网络推理相当于找到使分数最大化的结构。可能的图结构的数量与变量（测量的生物分子）的数量呈超指数关系，因此搜索空间的大小禁止穷举式搜索【会导致NP-难问题】。因此，我们采用启发式的模拟退火搜索。我们定义了一个搜索空间，其中每个状态都是一个可能的网络结构，并定义了一组操作符：增加、删除或扭转一个单一的弧，将网络从一个结构转变为另一个结构。我们从一个初始的随机结构开始，使用运算符遍历这个空间，寻找高分网络。在搜索过程中的每一步，我们用一个随机的算子来改变图形，对所产生的结构进行重新计分，如果该变化能提高分数，则将其纳入其中（为了避免局部最大值，偶尔也会纳入一个变化，即使它降低了分数）。我们反复进行这一程序以找到高分的图。

这个过程用不同的随机图来初始化，并重复（500次），以探索搜索空间的不同区域。通常情况下，所产生的许多模型对数据的解释几乎相同。为了在我们的推断中获得统计上的稳健性，而不是依赖单一的高分结构，我们对高分网络的汇编进行模型平均化（6）。这导致了一个由共同特征（弧）组成的平均网络，大多数高分网络结构在此基础上达成一致。最终推断出的网络由置信度在85%以上的弧组成（即至少在85%的高分网络中出现）。

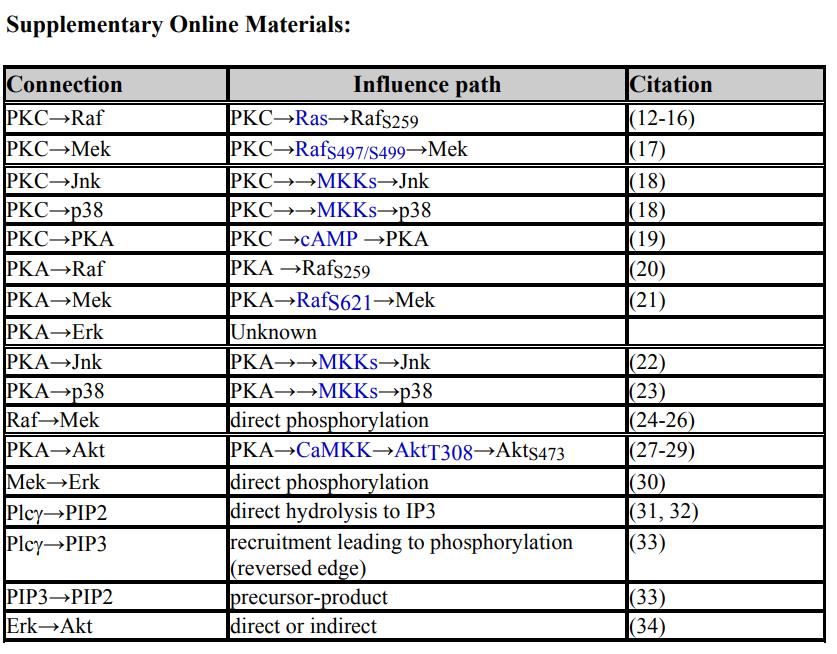
↑ SOM表1 
表1C中列出的可能的影响途径的引文。连接和影响路径如表1C所示（为方便起见在此重复）。

SOM 图1. 所用多色流式细胞仪数据的散点图示例。散点图中的每个点代表单个细胞中两个磷酸化蛋白的数量。A. 磷酸化蛋白Raf和Mek的散点图显示了明显的相关性，类似于图1C面板a中的模拟数据。 B. PKC和PKA的散点图显示了一个更嘈杂的依赖关系，用眼睛看不出来。所用的数据包含该图中两个例子之间的整个范围。鉴于有足够的数据，贝叶斯网络能够克服噪音并提取这些关系。

 

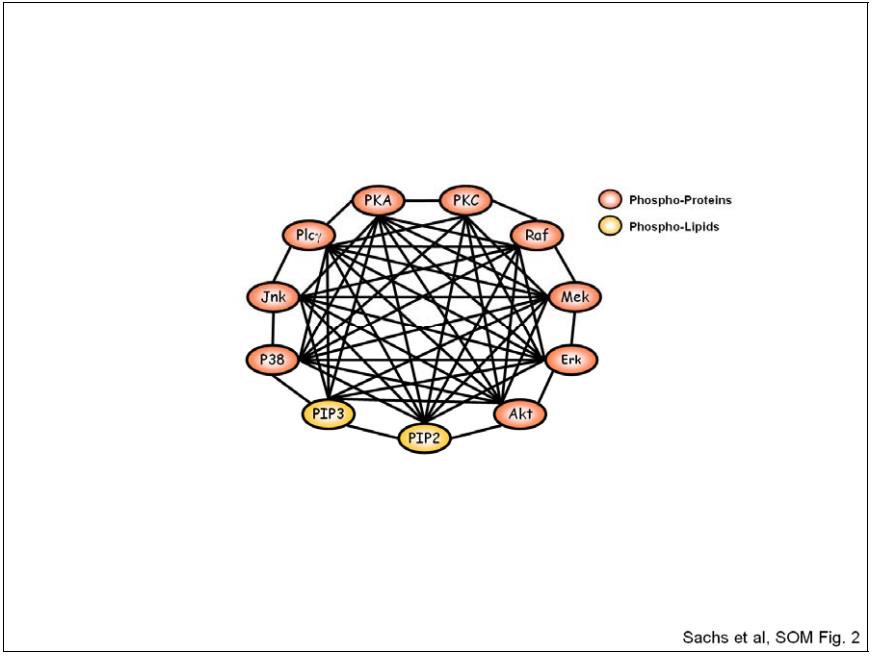
SOM 图2. 通过Bonferroni校正的P值的相关连接。在55个可能的弧中出现了52个。只有Pip3-Raf、Pip3-PKC和PKC-Jnk这几对没有发现显著的相关性。请注意，相关关系是没有方向的。因此，有必要应用更严格的测试（贝叶斯网络推理）来超越简单的相关性。

 

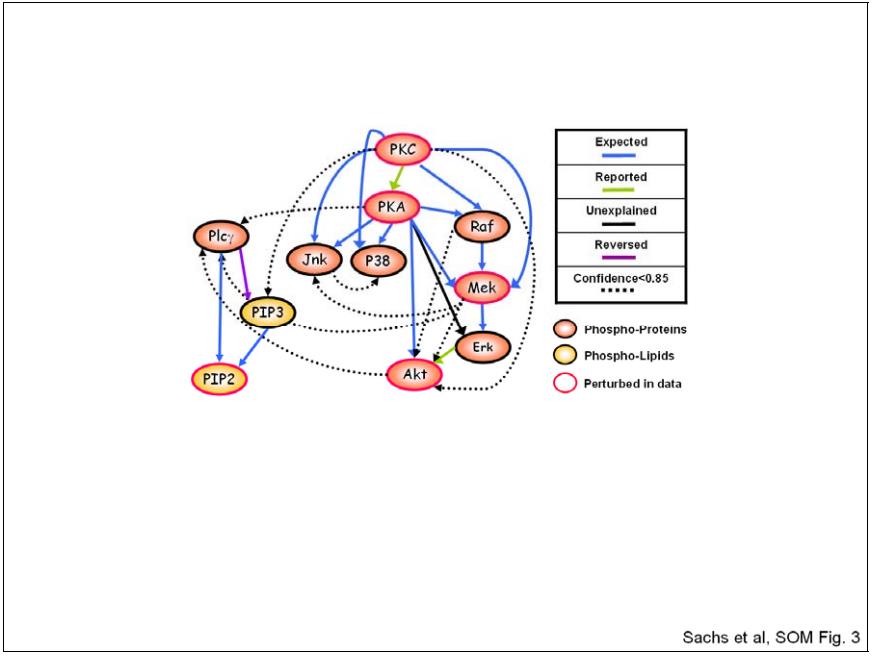
SOM 图3. 包括低置信度弧的推断结果。图中显示的是置信度为0.5或更高的弧。较低置信度的弧显示，每个缺失的弧（来自图3A）都可以通过非周期性约束来解释。缺少的弧Plcγ→PKC被路径PKC→PKA→Plcγ所排除，因为缺少的Plcγ→PKC弧的加入会在模型中形成一个循环。同样，PIP2→PKC的弧被PKC→PKA→Plcγ→PIP2的路径排除，PIP3→Akt被Akt→Plcγ→PIP3的路径排除。缺失的弧Akt→Raf被（高置信度）路径Raf→Mek→Erk→Akt排除，但它在反向（Raf→Akt）方向上出现了一个低置信度弧。缺少的电弧清楚地表明，由于非周期性约束，贝叶斯网络推理在生物路径上的应用受到限制。

SOM图4。干预性数据、大数据集规模和单细胞分辨率对有效推理至关重要。A. 观察性数据的推断结果表明，干预性数据对有效推断至关重要。贝叶斯网络分析被应用于一般刺激条件下的1200个数据点。结果网络中的预期弧数只有一半，而遗漏弧数几乎是完整数据对应的三倍（图3A）。此外，虽然有时可以仅用观察数据来检测有向弧，但在这种情况下，没有发现有向弧，所以该模型没有提供关于每个链接的因果方向的信息。B. 完整数据集的截断版本的结果显示了非常大的数据集规模的重要性。尽管这个数据集包含了完整数据集中的所有干预措施，但与完整数据集的结果相比，其较小的规模（420个数据点）导致了较少的预期连接恢复和更多的缺失弧（图3A）。C. 来自平均的、模拟的西方印迹数据的结果表明了单细胞分辨率的优势。模拟Western blot数据是通过一次平均20个随机选择的单细胞数据点来创建的，产生了一个420个点的数据集。与同等大小的单细胞数据集相比（SOM图4B），这个结果遗漏了更多的弧线，并捕获了更多未确认的弧线。做了十套截断和平均的数据集；B和C中的结果代表了典型的结果。

 【总结】

不愧是Science上的论文啊，

1.有非常Solid的生物实验，生成了自己的数据集。

2.并且结合了大量已有的论文结果作为自己的“数据集检验“，生物上的引用文献很convincing

3.利用的因果方法至少在当时是很有代表性且很有意义的，

文章八页我只草草读就已经比我之前认真细读的11页论文的导读blog长了，更何况还有这么多support material，这相当于八页顶了人家三四十页了吧？！不知道有没有源码，先去看看数据集吧。