论文导读Causal Protein-Signaling Networks Derived from Multiparameter Single-Cell Data

Posted 2022-04-19 ViviranZ

就离谱，我本来想研究因果+机器学习，却因为数据集被迫看生物的论文……

whatever，先看看吧

【介绍】这是2005年发表于science的一篇因果学习生物的论文，主要是想看看DAG-GNN到底怎么处理的实际数据集……Science的论文是真的Solid啊八页感觉比40多页还难读……希望论文讲讲处理数据集吧求求了孩子要毕不了业了！！！！！！！

原文提到的数据集是这样的：

We consider a bioinformatics data set (Sachs et al., 2005) for the discovery of a protein signaling network based on expression levels of proteins and phospholipids. This is a widely used data set for research on graphical models, with experimental annotations accepted by the biological research community. The data set offers continuous measurements of expression levels of multiple phosphorylated proteins and phospholipid components in human immune system cells, and the modeled network provides the ordering of the connections between pathway components. Based on n = 7466 samples of m = 11 cell types, Sachs et al. (2005) estimate 20 edges in the graph

粗读开始！

摘要

机器学习被应用于细胞信号传导网络中因果影响的自动推导。这种推导依赖于对数千个单个人类免疫系统细胞中的多种磷酸化蛋白质和磷脂成分的同时测量。用分子干预措施扰乱这些细胞，推动了通路成分之间的连接排序，其中贝叶斯网络计算方法自动阐明了大多数传统报道的信号关系，并预测了新的通路间网络因果关系，我们通过实验验证了这一点。从生理相关的原始单细胞中重建网络模型，可能会被应用于理解原生状态的组织信号生物学、复杂的药物作用和病变细胞中的功能障碍信号。

绪论

细胞外的线索引发了一连串的信息流，其中信号分子在化学上、物理上或位置上发生了变化；获得了新的功能能力；并影响到级联中的后续分子，最终形成了表型的细胞反应。信号通路的绘制通常涉及对来自不同实验系统的单个通路成分研究的汇总所产生的直观推断。尽管通路通常被概念化为对特定触发器作出反应的不同实体，但现在人们认识到，通路间的交叉对话和网络的其他特性反映了潜在的复杂性，这些复杂性不能通过孤立地考虑单个通路或模型系统来解释。为了正确理解正常的细胞反应和它们在疾病中的潜在失调，需要一个全球性的多变量方法（1）。贝叶斯网络（2），一种图形模型的形式，已被认为是一个有前途的框架，用于模拟复杂的系统，如细胞信号级联，因为它们可以表示多个相互作用的成分之间的概率依赖关系（3-5）。贝叶斯网络模型以影响图的形式说明了通路成分之间的影响（即通路中每个生物分子对其他生物分子的依赖）。这些模型可以通过一个有统计学基础的计算程序（称为网络推理）从实验数据中自动得出。尽管这些关系是统计学性质的，但当使用干预性数据时，它们有时可被解释为因果影响联系；例如，使用激酶特异性抑制剂（6，7）。

【阐述因果联系的来源：解释细胞外的线索---信息流---信号分子新的功能能力---后续分子---细胞反应的一溜关系】

贝叶斯网络在从生物数据集推断信号通路方面有几个吸引人的特性。贝叶斯网络可以表示多个相互作用的分子之间复杂的随机非线性关系，其概率性质可以容纳生物数据中固有的噪音。它们可以描述直接的分子相互作用以及通过额外的未观察到的成分进行的间接影响，这一特性对于发现以前的未知效应和未知成分至关重要。因此，可能存在于信号通路结构中的非常复杂的关系可以被建模和发现。贝叶斯网络推断算法构建了一个图示，其中节点代表被测量的分子，弧线（在节点之间画成线）代表这些分子之间有统计学意义的关系和依赖关系。当从实验数据中推断出贝叶斯网时，网络推断算法的目的是找出一个能密切预测所做观察的模型。该算法通过穿越可能性空间来接近最可能的模型，通过单弧度变化来提高分数。在简单的模型和那些准确捕捉数据中观察到的经验分布的模型之间有一个权衡。所采用的贝叶斯评分标准捕捉到了这种权衡；因此，一个高分的模型既是简单的，又是准确的数据代表（8，9）。贝叶斯网络已被应用于基因表达数据，用于研究和发现遗传调节途径（4，6，10）。然而，由于贝叶斯建模方法的概率性质，有效的推理需要对系统进行许多观察。因此，这类研究经常受到数据集规模不足的限制；例如，那些基于来自异质细胞群的平均样本的测量（当使用大量细胞的裂解物时，这是一个必要的限制）（5，11）。

【贝叶斯的好处：可以表示复杂的关系、可能识别间接的影响】PS：好牛啊这是我现在学的东西吗

 与基于裂解液的方法相比，细胞内多色流式细胞仪（12，13）可以更定量地同时观察成千上万个单个细胞中的多个信号分子。因此，对于信号通路的贝叶斯网络建模来说，它是一个特别合适的数据来源；例如，因为它可以在更多的原始背景下同时测量生物状态，也可以测量大的样本集。流式细胞仪可以用来定量测量一个给定的蛋白质表达水平，也可以包括蛋白质修饰状态的测量，如磷酸化（13-15）。因为每个细胞都被当作一个独立的观察对象，流式细胞仪数据提供了一个统计学上的大样本，可以使贝叶斯网络推理准确地预测路径结构（图1A）。正如本文所展示的，在单细胞群中询问信号网络提供了一个强大的统计学依赖性来源，可用于使用贝叶斯网络计算来自动推断信号的因果关系。

【主要讲的是为什么采用这个工具——细胞内多色流式细胞仪intracellular multicolor flow cytometry，因为它定量、范围更广、提供一个更大的样本】

用多变量个体细胞数据对贝叶斯网络进行建模  

Modeling Bayesian networks with multivariable individual-cell data.

图1B（面板a）展示了一个代表四个假设生物分子的贝叶斯网络样本。从X到Y的有向弧被解释为从X到Y的因果影响；在这种情况下，我们说X是Y在网络中的 "父母"。在X激活Y的情况下，激活可以通过磷酸化状态读出，我们期望并观察到流式细胞仪测量的磷酸化水平的相关性（模拟数据见图1C，面板a）。对贝叶斯网络模型的因果解释至关重要的是纳入干预性线索（无论是激活还是抑制），直接扰乱被测分子的状态（图1C，面板b）并加强推断的方向性。例如，对分子X的抑制可能导致对X和Y的抑制，而对分子Y的抑制只导致对Y的抑制，因此，我们会推断X是Y的上游，如图1B，面板a所示。考虑从X到Y到Z的信号级联（图1B，面板a），其中每一对的测量活性之间存在相关性，包括X和Z之间（图1c，面板d）。贝叶斯网络推理产生了最简洁的模型，自动排除了基于模型已经解释的依赖关系的弧。因此，尽管它们之间有相关性，但X和Z之间的弧被省略了，因为X-Y和Y-Z的关系解释了X-Z的相关性。同样，由于Z和W都被它们共同的原因Y激活，我们期望它们的活动是相关的，但它们之间没有弧出现，因为它们各自来自Y的弧调解了这种依赖关系。最后，考虑一种情况，在这种情况下，分子Y没有被测量。观察到的X和Z的活性之间的统计相关性并不取决于观察到的Y；因此，它们的相关性仍会被检测到。一个间接的弧线将被检测到，从X到Z（图1B，面板b）。

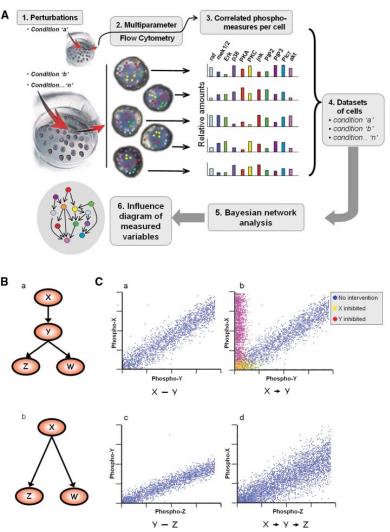
 图1. 用单细胞数据进行贝叶斯网络建模。(A）使用多维流式细胞仪数据的贝叶斯网络推理示意图。九种不同的扰动条件被应用于单个细胞组（表1）。一个多参数流式细胞仪同时记录了每个扰动数据组中单个细胞的11种磷蛋白和磷脂的水平（表2）。该数据集被置于贝叶斯网络分析中，它提取了一个影响图，反映了基础信号网络中的依赖性和因果关系。(B) 假设的蛋白质X、Y、Z和W的贝叶斯网络。(a) 在这个模型中，X影响Y，而Y又影响Z和W。(C) 可以重建(B)中的影响连接的模拟数据（这是贝叶斯网络运作方式的简化演示）。散点图中的每个点代表单个细胞中两个磷酸化蛋白的数量。(a) 磷酸化X和Y的模拟测量的散点图显示了相关性。(b) 干预性数据决定了影响的方向性。X和Y在没有操作的情况下是相关的（蓝点）。抑制X会影响Y（黄点），抑制Y不会影响X（红点）。这一起表明，X与作为上游父节点是一致的。(c) Y和Z的模拟测量。 (d) 在X和Z的模拟测量之间观察到一个嘈杂但明显的相关性。

 【主要阐释了这个图的运行规律，感觉很实用，因为因果最大的”困境“就是反事实推理，但是这个地方是做实验所以天然地不会陷入这个困境！这样目标就集中在学习到一个reasonable的因果关系图就可以了！】

将这一概念扩展到一个真实的数据集，我们将贝叶斯网络分析应用于多变量流式细胞仪数据。在一系列刺激性提示和抑制性干预（表1）后收集数据，在刺激后15分钟停止细胞反应的固定，以剖析每个条件对人类原始naıve CD4þ T细胞的细胞内信号网络的影响，在CD3、CD28和LFA-1激活的下游（图2显示目前公认的共识网络）。我们对11种磷酸化蛋白和磷脂进行了流式细胞仪测量[Raf在S259位置磷酸化，丝裂原活化蛋白激酶（MAPKs）Erk1和Erk2在T202和Y204位置磷酸化。p38 MAPK在T180和Y182位置磷酸化，Jnk在T183和Y185位置磷酸化，AKT在S473位置磷酸化，Mek1和Mek2在S217和S221位置磷酸化（该蛋白的两种异构体被同一抗体识别）。蛋白激酶A（PKA）底物[cAMP反应元件结合蛋白（CREB）、PKA、钙/钙蛋白依赖性蛋白激酶II（CaMKII）、caspase-10和caspase-2]的磷酸化，含有共识磷酸化图案。磷脂酶C-g（PLC-g）在Y783上的磷酸化，PKC在S660上的磷酸化，磷脂酰肌醇4,5-二磷酸（PIP2）和磷脂酰肌醇3,4,5-三磷酸（PIP3）] （表2）（8，16）。该数据集的每个独立样本包括11个磷酸化分子中每个分子的定量，同时从单细胞中测量[数据集可下载（8）]。为了说明问题，图中显示了实际的荧光激活细胞分拣机（FACS）数据的例子，以预期的核心关系形式绘制。S1. 在大多数情况下，这反映了所监测的激酶的激活状态，或者在PIP3和PIP2的情况下，在测量的条件下，这些次级信使分子在初级细胞中的水平。使用了九个刺激性或抑制性的干预条件（表1）（8）。完整的数据集用贝叶斯网络结构推理算法进行分析（6, 9, 17）。

图2. 经典的信号传导网络和干预点。这是对传统接受的信号分子相互作用、测量的事件和小分子抑制剂的干预点的图解。彩色的信号结点是直接测量的。灰色的信号节点没有被测量，但提出来是为了把被测量的信号节点放在背景细胞通路中。被归类为激活剂的干预措施用绿色表示，抑制剂用红色表示。图中指出了干预措施的作用部位。弧线用来说明信号分子之间的联系；在某些情况下，这种联系可能是间接的，可能涉及信号分子的特定磷酸化位点（这些联系的细节见表3）。该图包含了哺乳动物细胞中信号传导的概要，并不代表所有的细胞类型，其中肌醇信号传导的核心关系特别复杂。

 

表1. 已知采用的扰动的生物效应。左边一栏列出了每个扰动条件下使用的具体试剂，右边一栏将试剂类别划分为整体刺激细胞的一般扰动或作用于一组确定的分子的特殊扰动。研究中使用的条件如下。(i) 抗CD3 þ抗CD28，(ii) 抗CD3/CD28 þICAM-2（细胞间粘附分子-2），(iii) 抗CD3/CD28 þU0126，(iv) 抗CD3/CD28 þAKT抑制剂，(v) 抗CD3/CD28 þG06976。(vi) 抗CD3/CD28 þ psitectorigenin, (vii) 抗CD3/CD28 þ LY294002, (viii) phorbol 12-myristate 13-acetate (PMA), and (ix) b2 cyclic adenosine 3¶,5¶-monophosphate (b2cAMP)。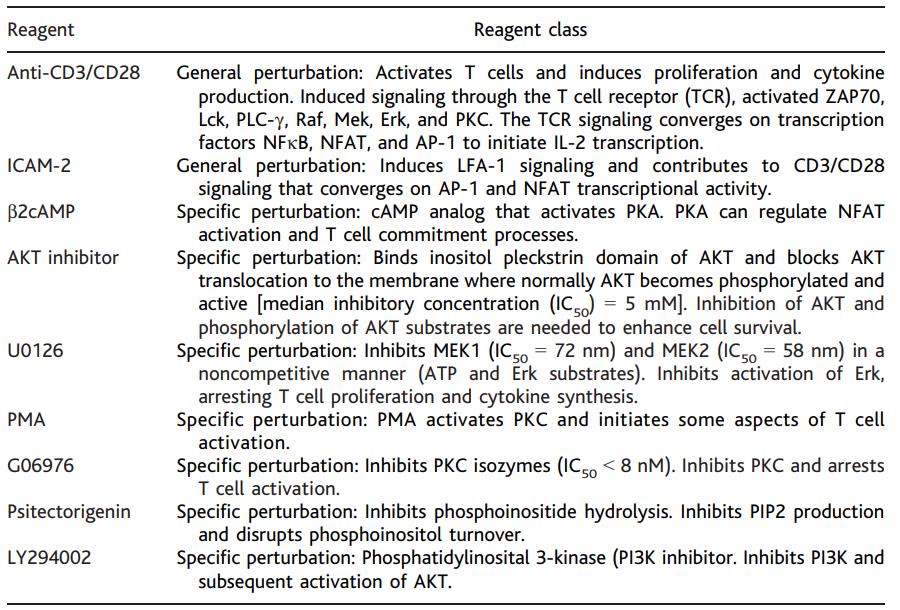

表2. 途径中测量的节点和使用的特异性抗体。左边一栏显示了本研究中测量的目标分子，这些分子使用目标残基（磷酸化部位或磷酸化产物，如所述）的单克隆抗体进行检测（16） 

表3. 模型中用弧线表示的可能的分子影响途径。所示为从数据中推断出的可能的影响途径，与图3A所示的联系以及可能介导间接影响的未测量的分子（黑体）。E，预期；R，报告。进一步讨论见主文。具体的磷酸化位点作为下标包括在内。支持这些推论的引文见表S1。 

 

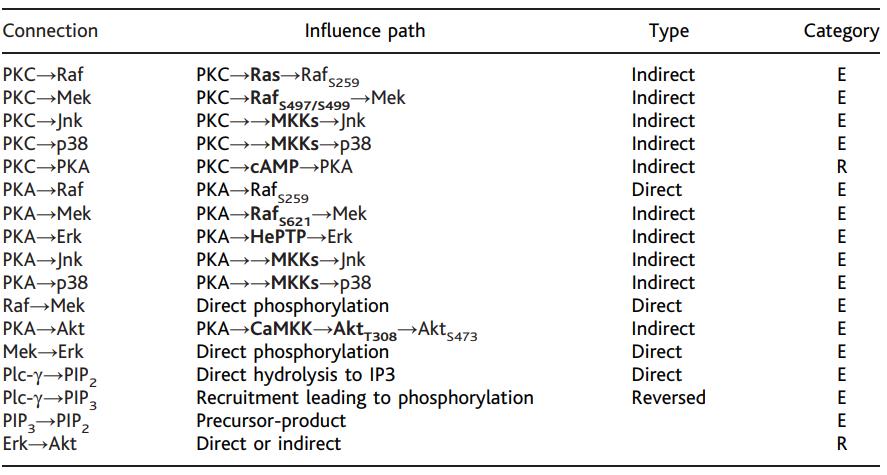
【这个就很离谱，我完全搞不懂这些生物的名词，但是大概理解就是说几个蛋白和磷脂的变化、找这几个变化的关系】

数据集是这个（8）？！！离谱！！！！

高准确度的人类初级T细胞信号传导因果关系图。

A high-accuracy human primary T cell signaling causality map

由此推断出的新的因果网络模型（图3A），在各种成分之间有17个高置信度的因果弧。为了评估这个模型的有效性，我们将模型弧（和不存在的潜在弧）与文献中描述的弧进行了比较。弧被归类为以下几种情况。(i) 预期的，指的是文献中已经确立的、在多个模型系统中的许多条件下被证明的连接；(ii) 报告的，指的是不为人知的、但我们能够找到至少一个文献引用的连接；(iii) 缺失的，表示我们的贝叶斯网络分析未能发现的预期连接。在我们模型中的17个弧线中，15个是预期的，所有17个弧线都是预期的或报告的，3个是缺失的（图3A和表S1）（8，18-22）。表3列举了通过调查已发表的报告确定的模型弧所对应的可能的影响路径。 

我们模型中的几个已知联系是直接的酶-底物关系（图3B）（PKA到Raf，Raf到Mek，Mek到Erk，以及Plc-g到PIP2），还有一个是导致磷酸化的招募关系（Plc-g到PIP3）。几乎在所有情况下，因果影响的方向都被正确地推断出来了（一个例外是Plc-g到PIP3，在这种情况下，弧线被推断为相反方向）。所有的影响因素都包含在一个全局模型中；因此，电弧的因果方向经常被强制要求，以便这些电弧与模型中的其他成分一致。这些全局性的约束允许检测某些来自分子的因果影响，这些分子在我们的试验中没有被扰动。例如，尽管Raf在任何测量条件下都没有被扰动，但该方法正确地推断出了一个从Raf到Mek的有向弧，这对于特征明显的Raf-Mek-Erk信号转导途径来说是可以预期的。在某些情况下，一个分子对另一个分子的影响是由数据集中没有测量的中间分子介导的。在结果中，这些间接的联系也被检测到（图3B，b组）。例如，PKA和PKC对MAPKs p38和Jnk的影响可能是通过它们各自的（未测量的）MAPK激酶激酶进行的。因此，与其他一些用于阐明信号网络的方法[如蛋白质-蛋白质相互作用图（23，24）]不同，我们的贝叶斯网络方法可以检测到直接和间接的因果联系，因此提供了一个更有背景的信号网络图片。

【这两段主要介绍了一下实验的结果，第一段：有缺失的（存在弧没有被计算出来）；第二段：有错误的、也有特别nb没设置也给发现了的】

 图3. 贝叶斯网络推断结果。(A) 从流式细胞仪数据推断出的网络代表了预期结果。这个网络代表了500个高分结果的模型平均值。显示了至少85%的网络中出现的高置信度的弧。为清晰起见，分子的名称被用来代表测量的磷酸化位点（表2）。(B) 推断网络显示了贝叶斯网络的几个特点。(a) 网络中的弧可能对应于直接事件或(b)间接影响。(c) 当中间分子在数据集中被测量时，间接影响很少作为一个额外的弧出现。在Raf和Erk之间没有添加额外的弧，因为Raf和Erk之间的依赖性被Raf和Mek以及Mek和Erk之间的联系所否定（例如，见图1C）。(d) 模型中的连接包含磷酸化位点特异性信息。因为在我们的数据集中没有测量Raf在S497和S499的磷酸化，PKC和测量的Raf磷酸化位点（S259）之间的联系是间接的，可能是通过Ras进行的。PKC和未检测到的S497和S499上的Raf磷酸化之间的联系被视为PKC和Mek之间的一个弧线。

我们的模型的另一个特点是能够驳回已经被其他网络弧线解释的连接（图3B，c组）。这可以在RafMek-Erk级联中看到。Erk，又称p44/42，是Raf的下游，因此依赖于Raf，但没有出现从Raf到Erk的弧，因为从Raf到Mek的连接和从Mek到Erk的连接解释了Erk对Raf的依赖性。因此，只有当数据集中不存在一个或多个中间分子时，才会出现间接弧，否则连接将通过这个分子进行。中间分子也可能是一个共享的母体。例如，p38和Jnk的磷酸化状态是相关的（图S2），但它们没有直接的联系，因为它们共同的父母（PKC和PKA）介导了它们之间的依赖关系。虽然我们不能知道我们的模型中的一个弧代表了直接或间接的影响，但我们的模型不可能包含一个由我们测量中观察到的任何分子介导的间接弧。在这个数据集中的大多数分子对之间存在相关性[根据Bonferroni校正的P值（图S2）]，这可能发生在紧密连接的途径上。因此，我们的模型中相对缺乏弧线（图3A），这大大有助于推断模型的准确性和可解释性。

【一个例子解释，模型一般来说计算出来的弧比较少，（从而也能保证弧的可靠性）】

一个更复杂的例子是PKC对Mek的影响，已知它是由Raf介导的（图3B，面板d）。已知PKC通过两条影响路径来影响Mek，每条路径都由蛋白Raf的不同活性磷酸化形式介导。尽管PKC直接在S499和S497处使Raf磷酸化，但我们的测量没有检测到这一事件，因为我们只使用了对Raf在S259处磷酸化的特定抗体（表2）（16）。因此，我们的算法检测到一个从PKC到Mek的间接弧线，这个弧线是由假定的未测量的中间Raf在S497和S499处磷酸化介导的（18）。PKC到Raf的弧线代表了一种间接的影响，它通过一个未测量的分子进行，据推测是Ras（19，20）。我们在上面讨论了我们的方法能够排除多余的弧。在这种情况下，有两条路径从PKC通向Mek，因为每条路径都对应于从PKC到Mek的单独影响方式：一条是通过S259处磷酸化的Raf，另一条是通过S497和S499处磷酸化的Raf。因此，这两条路径都不是多余的。这一结果证明了这一分析对分子上特定的磷酸化位点是敏感的，并且能够检测到分子之间不止一个影响途径的区别。

【一个例子解释，模型中多条弧也是reasonable】

在我们的模型中没有出现三个公认的影响联系。PIP2到PKC，PLC-g到PKC，以及PIP3到Akt。贝叶斯网络被限制为非周期性的，所以如果基础网络包含反馈环路，我们不一定能期望发现所有的连接（图S3）。如果有合适的时间数据，可能会允许使用动态贝叶斯网络来克服这一限制（25，26）。

【无环啊无环 你是真的坑】

对预测的网络因果关系的实验确认。

Experimental confirmation of predicted network causality.

我们模型中的两个影响联系在文献中没有得到很好的证实。PKC对PKA和Erk对Akt。为了探究这些拟议的因果影响的有效性，我们在文献中搜索了一些报告。这两种联系以前都有报道：大鼠心室肌细胞中的PKC-PKA联系和结肠癌细胞系中的Erk-Akt联系（21，22）。我们工作的一个重要目标是测试流式细胞仪数据的贝叶斯网络分析能力，以正确推断网络内未受干扰分子的因果影响。例如，在样本集中，Erk没有被任何激活剂或抑制剂直接作用，但Erk却显示出与Akt的影响联系。因此，我们的模型预测，Erk的直接扰动会影响Akt（图4A）。另一方面，尽管Erk和PKA是相关的（图S2），该模型预测Erk的扰动不应该影响PKA。

作为对这些预测的测试（图3A），我们用小干扰RNA（siRNA）抑制Erk1或Erk2，然后测量S473磷酸化的Akt和磷酸化的PKA的数量。与模型预测一致，Akt（P G 9.4 10j5）的磷酸化在siRNA抑制Erk1后减少，但PKA（P G 0.28）的活性却没有（图3，B和C）。Akt的磷酸化不受Erk2抑制的影响。Erk1和Akt之间的联系可能是直接或间接的，涉及尚待了解的中介分子，但这种联系得到了模型和验证实验的支持。

【真的羡慕生物做因果的，出现问题还有一个实验基础，唉】

准确推断的有利因素：网络干预和足够数量的单细胞。

Enablers of accurate inference: network interventions and sufficient numbers of single cells.

有三个特点使我们的数据与目前可获得的大多数生物数据集不同。首先，我们同时测量了单个细胞中的多种蛋白质状态，消除了可能掩盖有趣相关性的群体平均效应。第二，由于测量是在单细胞上进行的，所以在每个实验中都收集了成千上万的数据点。这一特点构成了贝叶斯网络建模的巨大财富，因为大量的观测数据可以准确评估潜在的概率关系，因此可以从噪声数据中提取复杂的关系。第三，干预性试验在每次干预中产生了数百个单独的数据点（因为流式细胞仪测量的是群体中的单细胞），使得因果关系的推论得以增加。为了评估这些特征的重要性，我们在原始数据集上建立了以下变化。(i) 1200个数据点的纯观察数据集（即没有任何干预数据）；(ii) 群体平均（即模拟Western blot）数据集；以及(iii) 与模拟Western blot数据集大小相当的截断的单个细胞数据集（即原始数据集，随机排除大部分数据以减少其大小）(8)

【再次提到数据集啊啊啊啊啊啊让我找到它吧求求求求了！！！！】

对每组数据进行了贝叶斯网络推断。从1200个观察数据点推断出的网络只包括10条弧，都是无方向性的，其中8条是预期的或报告的，10条弧是缺失的（图S4A）。这一结果表明，干预措施对有效推断至关重要，特别是要建立连接的方向性（图1B）。截断的单细胞数据集（420个数据点）显示出准确性的大幅下降（11个弧），与较大的数据集（5400个数据点）相比，遗漏了更多的连接，并报告了更多无法解释的弧（图S4B）。这一结果强调了足够大的数据集规模在网络推断中的重要性。从平均数据推断出的网络（图S4C）显示，相对于从同等数量的单细胞数据点推断出的网络，其准确性又下降了5个弧，强调了单细胞数据的重要性。群体平均化破坏了数据中存在的一些信号，这一事实可能反映了异质细胞亚群的存在，这些亚群被平均化技术所掩盖。 

【数据分析，生物的，略】

 

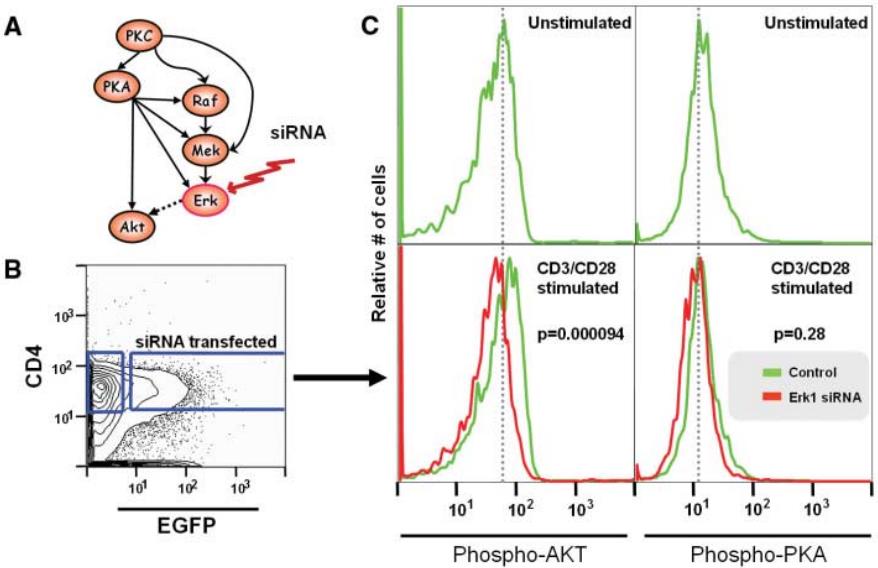
图4. 对模型预测的验证。(A) 该模型预测，对Erk的干预将影响Akt，但不影响PKA。(B) 为了测试预测的关系，在用CD3抗体（抗CD3）和抗CD28刺激的细胞中，用siRNA抑制了Erk1和Erk2。(C) 评估转染的CD4þ细胞[增强型绿色荧光蛋白（EGFPþ）细胞]中Akt磷酸化的数量，并将磷酸化的PKA数量作为阴性对照。当Erk1表达被抑制时，磷酸化的Akt减少到与未刺激的细胞相似的数量，证实了我们的预测（P 0 0.000094）。PKA不受影响（P0 0.28）。

讨论和总结

如图所示，我们正确地逆向设计并快速推断了一个经典理解的信号网络的基本结构，该网络连接了人类T细胞信号转导中的一些关键磷酸化蛋白，这是过去二十年来通过经典的生物化学和遗传分析建立的地图。该网络是自动构建的，没有关于通路连接的先验知识。贝叶斯网络在单细胞流式细胞仪中的应用具有明显的优势，包括能够测量体内干预后的原生细胞事件（从而测量组织中特定的信号生物学），推断定向弧和其中的因果关系，以及检测间接和直接连接的能力。当已知的参与分子列表可能并不详尽时，后一点是一个强大的功能，当网络被用来评估系统扰动的影响时（如在制药方面），这一点可能特别重要。实验中的一个限制性步骤是合适的试剂的可用性；目前，大约有80种与流式细胞仪兼容的磷酸化分子的抗体，但这个数字预计会迅速增加（27，28）。

【哈哈哈哈我们做了一个很nb的工作！我们搞了一个可以自动构建的网络、分析磷酸化蛋白！不过贝叶斯网络分析…………】

将这种方法应用于其他的分子集、细胞类型、疾病状态和干预措施（例如，siRNA和显性阴性筛选，或药物制剂），应能加强我们对信号网络的理解，特别是对通路之间复杂的非线性交叉对话的理解。这种方法可以解决的另一个重要的实验问题是特定的原始细胞类型和细胞亚群之间的差异。从不同的模型细胞类型和生物体中整理出来的对通路结构的传统理解，显示了基本信号网络的基本一致性，但不容易揭示不同原代细胞亚型中存在的微妙差异。现在有可能在原生细胞亚群中体会到路径的错综复杂，包括那些具有以前未被描述的信号分子。在疾病状态下或在药物作用下对细胞亚群特异性信号网络进行生化审讯时，应用这种方法有可能提供与临床相关的重要机制信息。例如，这种方法可以确定一些信号分子，解释癌症患者对化疗反应的差异（15）。

【我跟你们说哦，我们这个还可以用在别的数据集！！！】

关于计算方面，贝叶斯网络的一个关键优势是它们对未观察到的变量的存在相对稳健；例如，它们通过未测量的分子检测间接影响的能力。贝叶斯网络研究的最前沿是开发自动推断这种隐藏变量的存在和位置的方法。虽然我们的结果仅限于每个细胞11个磷分子的测量，但流式细胞仪同时测量的参数数量正在稳步增长（27，28）。随着测量系统的改进，以及随时准确测量更多内部信号事件的能力增加，发现新的影响因素和途径结构的更多机会成为可能。

【贝叶斯我们用的很可靠哦！】

使用贝叶斯网络来阐明信号通路的注意事项之一是，它们被限制为非周期性的，而众所周知，信号通路富于反馈回路。事实上，我们的推断错过了三个经典的弧线，很可能就是这个原因。鉴于时间序列数据，动态贝叶斯网络有可能捕获这些反馈环路。为了测量内部磷酸化蛋白的数量，细胞必须被固定。因此，连续的、实时的、同步的、多参数的、单细胞的时间序列数据不能用目前的技术来收集。因为贝叶斯网络属于一类更普遍的概率图解模型，在这些模型的形式主义中，有可能开发出一个可以处理反馈回路的模型，给定一系列的静态时间点，使用目前的技术。

【贝叶斯有点限制……无环，或许可能反馈回路也可以加入？（这个我们现在都没搞明白呢！17年了大清都亡了怎么处理反馈回路还是不知道，控制系统？）】

 尽管在计算和实验方面还有很多需要发展的地方，但通过扩展这里得出的概念，很明显，对多个离散实体（如细胞）的生物状态进行同步多变量分析，为快速得出信号网络层次和结构提供了一个有用的方法。将这种方法扩展到涉及多个细胞群的生物系统，如实体组织和器官，或整个动物研究，如在分阶段的优雅凯诺虫或果蝇幼虫的磷酸化状态的全身荧光成像，或哺乳动物器官的薄片组织切片，可以在越来越多的生理背景下，不仅在细胞内，而且跨细胞边界自动构建信号网络的影响。

【Anyway，我们是一个超厉害的方法！】

Reference：

 

1. T. Ideker, T. Galitski, L. Hood, Annu. Rev. Genom. Human Gen. 2, 343 (2001).

2. J. Pearl, Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference (Morgan Kaufmann, San Mateo, CA, 1988).

3. N. Friedman, Science 303, 799 (2004).

4. N. Friedman, M. Linial, I. Nachman, D. Pe’er, J. Comput. Biol. 7, 601 (2000).

5. K. Sachs, D. Gifford, T. Jaakkola, P. Sorger, D. A. Lauffenburger, Sci. STKE 2002, pe38 (2002).

6. D. Pe’er, A. Regev, G. Elidan, N. Friedman, Bioinformatics 17 (suppl. 1), S215 (2001).

7. J. Pearl, Causality: Models, Reasoning, and Inference (Cambridge Univ. Press, Cambridge, 2000).

8. Materials, methods, and an outline of Bayesian modeling are available as supporting material on Science Online.

9. D. Pe’er, Sci. STKE 2005, pl 4 (2005).

10. A. J. Hartemink, D. K. Gifford, T. S. Jaakkola, R. A. Young, Pac. Symp. Biocomput. 2001, 422 (2001).

11. P. J. Woolf, W. Prudhomme, L. Daheron, G. Q. Daley, D. A. Lauffenburger, Bioinformatics 21, 741 (2005).

12. L. A. Herzenberg, D. Parks, B. Sahaf, O. Perez, M. Roederer, Clin. Chem. 48, 1819 (2002).

13. O. D. Perez, G. P. Nolan, Nat. Biotechnol. 20, 155 (2002).

14. O. D. Perez et al., Nat. Immunol. 11, 1083 (2003).

15. J. M. Irish et al., Cell 118, 217 (2004).

16. Single-letter abbreviations for the amino acid residues are as follows: S, Ser; T, Thr; and Y, Tyr.

17. D. Heckerman, in Learning in Graphical Models, M. I. Jordan, Ed. (MIT Press, Cambridge, MA, 1998), pp. 301–354.

18. M. P. Carroll, W. S. May, J. Biol. Chem. 269, 1249 (1994).

19. R. Marais, Y. Light, H. F. Paterson, C. J. Marshall, EMBO J. 14, 3136 (1995).

20. R. Marais et al., Science 280, 109 (1998).

21. W. M. Zhang, T. M. Wong, Am. J. Physiol. 274, C82 (1998).

22. R. Fukuda, B. Kelly, G. L. Semenza, Cancer Res. 63, 2330 (2003).

23. M. Steffen, A. Petti, J. Aach, P. D’haeseleer, G. Church, BMC Bioinformat. 3, 34 (2002).

24. B. P. Kelley et al., Nucleic Acids Res. 32, W83 (2004).

25. K. M. Nir Friedman, S. Russell, Proceedings of the Fourteenth Annual Conference on Uncertainty in Artificial Intelligence (Morgan Kaufmann, San Francisco, 1998).

26. J. D. G. Irene, M. Ong, D. Page, Bioinformatics 18, S241 (2002).

27. M. Roederer, J. M. Brenchley, M. R. Betts, S. C. De Rosa, Clin. Immunol. 110, 199 (2004).

28. A. Perfetto, P. Chattopadhyay, M. Roederer, Nat. Rev. Immunol. 4, 648 (2004).

29. The authors thank G. Church, N. Friedman, J. Albeck, P. Jasper, L. Garwin, R. Tibshirani, T. Jaakkola, D. Gifford, and D. Koller for helpful discussions or readings of the manuscript and R. Balderas and BD-PharMingen Biosciences for reagents. K.S. and D.A.L. were supported by the National Intitute of General Medical Sciences Center of Excellence in Complex Biomedical Systems at MIT. O.D.P. was supported as a Bristol-Meyer Squibb Irvington Fellow and a Dana Foundation human immunology award. D.P. was supported by a PhRMA Center of Excellence in Integration of Genomics and Informatics grant, an NIH Center of Excellence in Genomic Studies grant to G. Church, and an NSF Postdoctoral Research Fellowship in Biological Informatics. G.P.N. was supported in this work by NIH grants P01-AI39646 and AI35304, a grant from the Juvenile Diabetes Foundation, and National Heart, Lung, and Blood Institute Proteomics Center contract N01-HV-28183I.

找到online material了！！！在最后面！！！！！冲鸭！！！！！！！！！！！！！！！