数字信号处理1：卷积

Posted 2022-12-12 zuguorui

文章目录

• 一、前言
• 二、线性时不变（LTI）系统
• 三、冲激函数
• 四、阶跃函数
• 五、卷积
• • 5.1 卷积的推导
  • 5.2 LTI系统卷积的性质
  • • 5.2.1 交换律
    • 5.2.2 分配律
    • 5.2.3 结合律

数字信号处理是音视频开发所必不可少的一项技能，我会从本篇开始，开启一系列入门文章，分享关于数字信号处理方面的知识。这只是一个精简的知识提炼，供大家进行入门，也是对自己的一个备忘和学习笔记。难免会有纰漏，要深入的同学请务必去看一些经典教材。

文章以 * 来表示乘法，以$\otimes 表示卷积$

一、前言

数字信号处理我们日常生活中其实会经常接触到，像音频、视频、机械控制等等。简单来说就是一个信号$x$，通过系统$S$后输出信号$y$，系统$S$需要对信号进行处理，比如滤除噪音、调节频率等等。数字信号处理讲的就是对$x$进行操作的学问。

二、线性时不变（LTI）系统

一般我们说数字信号处理都是基于线性时不变（LTI）系统，那么什么是LTI系统呢？顾名思义
1. 线性： 这个线性其实就是我们所用的线性方程中的那个概念，满足叠加定理，比如$x_1\to y1$是一个映射（也就是我们常说的函数关系）。假设有$x_2=a{x}_1$，经过同样的映射$x_2\to y_2$，那么$y_2=a{y}_1$。

2. 时不变： 这个就更好理解了。同样一个输入信号，任何时候的输出都是一样的。

三、冲激函数

冲激函数是指在0点上有值，而在其他地方均为0的函数。通常使用$\delta$表示。

连续形式：
$$\delta (t)=\begin{array}{ll}+\infty & t=0\\ 0& t\ne 0\end{array}$$

上面的式子比较抽象，其实它只有一个定义，就是在负无穷到正无穷的积分是1。

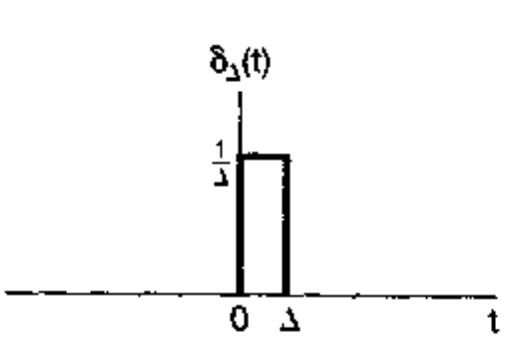
离散形式：
$$\delta [n]=\begin{array}{ll}1& n=0\\ 0& n\ne 0\end{array}$$

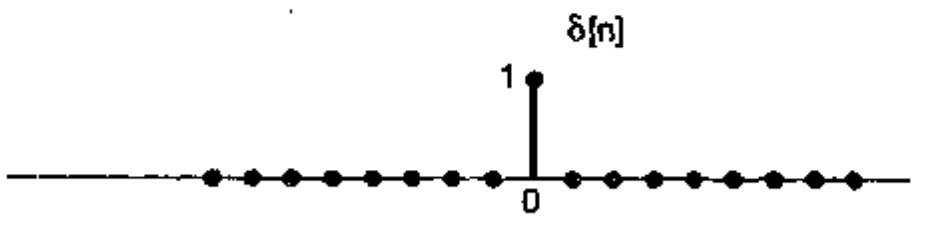
它们各有一些性质，不过我们马上使用的是一些直观上的数学性质。

需要说明的一点，之后我们推导的很多公式都会以连续信号和离散信号的形式。连续信号我们以$x(t)$表示，离散信号我们以$x[n]$表示

四、阶跃函数

阶跃函数是从0开始到正无穷都为1，从负无穷到0都为0的函数。

连续形式：

$$u(t)=\begin{array}{ll}1& t>0\\ 0& t<0\end{array}$$

需要注意的是，阶跃函数在t=0这一点是不连续的。
连续的阶跃函数和冲激函数有这么一层关系，从上面讲的连续冲击函数的定义，就可以得出
$$u(t)={\int }_{-\infty }^t\delta (\tau )d\tau$$
因为$\delta (t)$在负无穷到正无穷的积分是1。那么$\delta (t)$就是$u(t)$的一阶微分。但上面也说过$u(t)$在t=0时是不连续的，因此严格来说不是可导的。但如果将$u(t)$认为是在一个很小的间隔$\Delta$内从0上升到1的，那就不难理解了。而这种情况，其实在现实世界中才是真正常见的。

离散形式：
$$u[n]=\begin{array}{ll}1& n\ge 0\\ 0& n<0\end{array}$$

显然离散形式要简单多了。同连续形式，我们也可以得出离散的冲击函数和阶跃函数的关系。
$$u[n]=\sum _{m=-\infty }^n\delta [m]$$
$u[n]$是$\delta [n]$的求和
或者
$$\delta [n]=u[n]-u[n-1]$$
$\delta [n]$是$u[n]$的差分。

从以上形式不难看出一个规律，离散的求和对应连续的积分，离散的差分对应连续的微分，这一点将会在记忆一些性质的时候特别有用。后面我们也将会更加深刻地体验到。

五、卷积

5.1 卷积的推导

让我们以离散信号举例，从上面的冲激函数和阶跃函数来推导。
设有一信号
$$x[n]=...+x[-2]+x[-1]+x[0]+x[1]+x[2]+...$$
由于我们是从数学上来推导，因此暂且不要关心信号的序号为什么会有负的。
由冲激函数的定义，我们可以稍稍变形
$$x[i]=x[i]\ast \delta [n-i]$$
因为当且仅当$i=n$时$\delta [n-i]=1$
那么
$$\begin{gathered} x[n]=...+x[-2]\ast \delta [n+2]+x[-1]\ast \delta [n+1]+x[0]\ast \delta [n]+x[1]\ast \delta [n-1]+x[2]\ast \delta [n-2]+... \\ =\sum _{k=-\infty }^{+\infty }x以上是关于数字信号处理1：卷积的主要内容，如果未能解决你的问题，请参考以下文章 \end{gathered}$$

2.4时序卷积网络TCN：因果膨胀卷积残差连接和跳过连接

谈谈音频信号处理中 CNN 的因果性

数字信号处理线性时不变系统 LTI “ 输入 “ 与 “ 输出 “ 之间的关系 ( 周期性分析 | 卷积运算规律 | 交换律 | 结合律 | 分配率 | 冲击不变性 )

数字信号处理离散时间系统因果性 ( 因果性概念 | 充要条件及证明 )

一维与二维时间卷积网络深解(Temporal Convolutional Network,TCN)

keras 中的因果填充