2.4时序卷积网络TCN:因果膨胀卷积残差连接和跳过连接
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2.4时序卷积网络TCN:因果膨胀卷积残差连接和跳过连接相关的知识,希望对你有一定的参考价值。
对于序列问题(Sequence Modeling)的处理方法,通常采用RNN或者LSTM,例如处理一段视频/音频,往往会沿着时间方向(时序)进行操作。通常CNN网络都被认为适合处理图像数据而不适合处理sequence modeling问题,这主要由于其卷积核大小的限制,不能很好的抓取长时的依赖信息。而今年来,由于RNN及LSTM这类模型的瓶颈,越来越多的人开始发现其实CNN对于这种序列问题的处理是被大大低估了,CNN建立的model要比之前人们之前用的RNN要好很多,而且简洁。
时序卷积网络(TCN),是用于序列建模任务的卷积神经网络的变体,结合了 RNN 和 CNN 架构。对 TCN 的初步评估表明,简单的卷积结构在多个任务和数据集上的性能优于典型循环网络(如 LSTM),同时表现出更长的有效记忆。
TCN由因果膨胀卷积核残差块组成,实现没有从未来到过去的信息泄漏,并且网络查看非常远的过去以做出预测的能力,
问题描述
对音频进行生成,一个音频
x
=
{
x
1
,
…
,
x
T
}
\\mathbf{x}=\\left\\{x_{1}, \\ldots, x_{T}\\right\\}
x={x1,…,xT}的联合概率化为条件概率的乘积,如下:
p
(
x
)
=
∏
t
=
1
T
p
(
x
t
∣
x
1
,
…
,
x
t
−
1
)
(1)
\\large \\color{green}{p(\\mathbf{x})=\\prod_{t=1}^{T} p\\left(x_{t} \\mid x_{1}, \\ldots, x_{t-1}\\right)}\\tag{1}
p(x)=t=1∏Tp(xt∣x1,…,xt−1)(1)
因此,每个音频样本
x
t
x_{t}
xt都是基于之前所有时间步的样本。
条件概率分布是由一堆卷积层建模的。网络中没有池化层,模型的输出与输入具有相同的时间维度。该模型通过一个softmax层输出下一个值 x t x_{t} xt的分类分布,并对其进行优化,使数据的对数似然值最大化。由于对数似然是易于处理的,可以调整验证集上的超参数,并且可以很容易地测量模型是过拟合还是欠拟合。
因果卷积(causal Convolutions)
因果卷积可以解决序列问题。
图
1
:
因
果
卷
积
层
堆
叠
的
可
视
化
\\large \\color{green}{图1:因果卷积层堆叠的可视化}
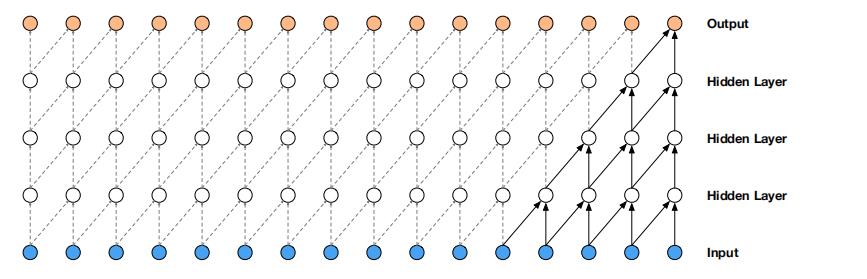
图1:因果卷积层堆叠的可视化
如图1所示,模型在时间步 t t t时发出的预测 p ( x t + 1 ∣ x 1 , … , x t ) p\\left(x_{t+1} \\mid x_{1}, \\ldots, x_{t}\\right) p(xt+1∣x1,…,xt) 不能依赖于任何未来的时间步 x t + 1 , x t + 2 , … , x T x_{t+1}, x_{t+2}, \\ldots, x_{T} xt+1,xt+2,…,xT。每一层的输出都是由前一层对应未知的输入及其前一个位置的输入共同得到,并且如果输出层和输入层之前有很多的隐藏层,那么一个输出对应的输入就越多,并且输入和输出离得越远。
对于图像,与因果卷积等价的是mask卷积,它可以通过构造mask张量并在应用它之前对该mask与卷积核进行逐项相乘来实现。对于文本等一维数据,可以通过将普通卷积的输出移动几个时间步来更容易实现这一点。
在训练时,对所有时间步长的条件预测可以并行进行,因为ground truth x \\mathrm{x} x的所有时间步长都已知。当模型测试时,预测是连续的:在每个样本被预测后,它被反馈到网络来预测下一个样本。
因果卷积通常比rnn训练得更快,特别是当应用于非常长的序列时。因果卷积的问题之一是,它们需要许多层,或大的filter来增加卷积的感受野。例如,在图1中,感受野仅为 5 ( = 5(= 5(= #layers + + + filter length − 1 ) . -1) . −1).。而卷积层数的增加就带来:梯度消失,训练复杂,拟合效果不好的问题。
所以就有了膨胀卷积,将感受野增加一个数量级。
膨胀因果卷积( dilated convolution)
膨胀卷积是通过跳过部分输入来使filter可以应用于大于filter本身长度的区域。等同于通过增加零来从原始filter中生成更大的filter。
图
2
:
膨
胀
的
因
果
卷
积
层
堆
叠
的
可
视
化
\\color{green}{图2:膨胀的因果卷积层堆叠的可视化}
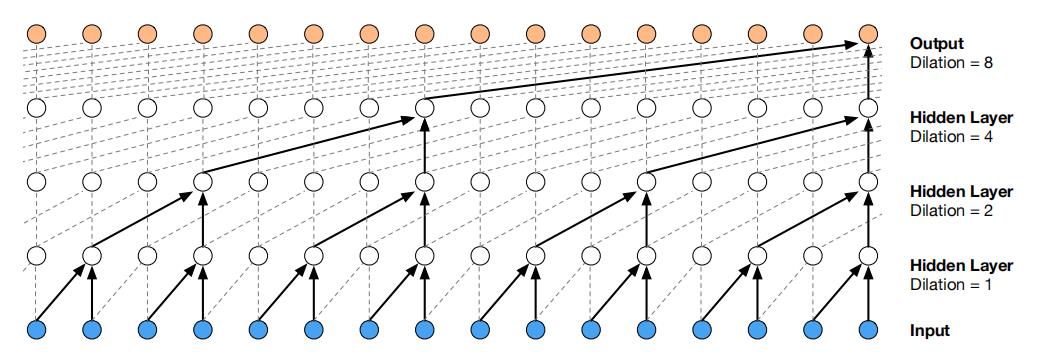
图2:膨胀的因果卷积层堆叠的可视化
图2描绘了膨胀1、2、4和8的膨胀因果卷积。
与普通卷积相比,膨胀卷积可以有效地使网络在更粗的尺度上运行。这类似于池化或跨越式卷积,但这里的输出与输入具有相同的大小。
一种特殊情况,膨胀系数1的膨胀卷积就是标准卷积了。堆叠膨胀卷积使网络仅用几层就能拥有非常大的感受野。训练过程,每一层的膨胀倍数达到一个极限,然后重复,即
1
,
2
,
4
,
.
.
.
,
512
,
1
,
2
,
4
,
.
.
.
,
512
,
1
,
2
,
4
,
.
.
.
,
512.
1, 2, 4, . . . , 512, 1, 2, 4, . . . , 512, 1, 2, 4, . . . , 512.
1,2,4,...,512,1,2,4,...,512,1,2,4,...,512.
看图3更清楚.

图 3 : 膨 胀 的 因 果 卷 积 训 练 过 程 \\color{green}{图3:膨胀的因果卷积训练过程} 图3:膨胀的因果卷积训练过程
门控激活
使用门控激活单元
z
=
tanh
(
W
f
,
k
∗
x
)
⊙
σ
(
W
g
,
k
∗
x
)
(2)
\\large \\color{green}{\\mathbf{z}=\\tanh \\left(W_{f, k} * \\mathbf{x}\\right) \\odot \\sigma\\left(W_{g, k} * \\mathbf{x}\\right)}\\tag{2}
z=tanh(Wf,k∗x)⊙σ(Wg,k∗x)(2)
其中
∗
*
∗表示卷积运算符,
⊙
\\odot
⊙表示元素级的乘法运算符,
σ
(
⋅
)
\\sigma(\\cdot)
σ(⋅)是sigmoid函数,
k
k
k是层索引,
f
f
f和
g
g
g分别表示卷积核和门,
W
W
W是可学习的参数。
残差连接和跳过连接
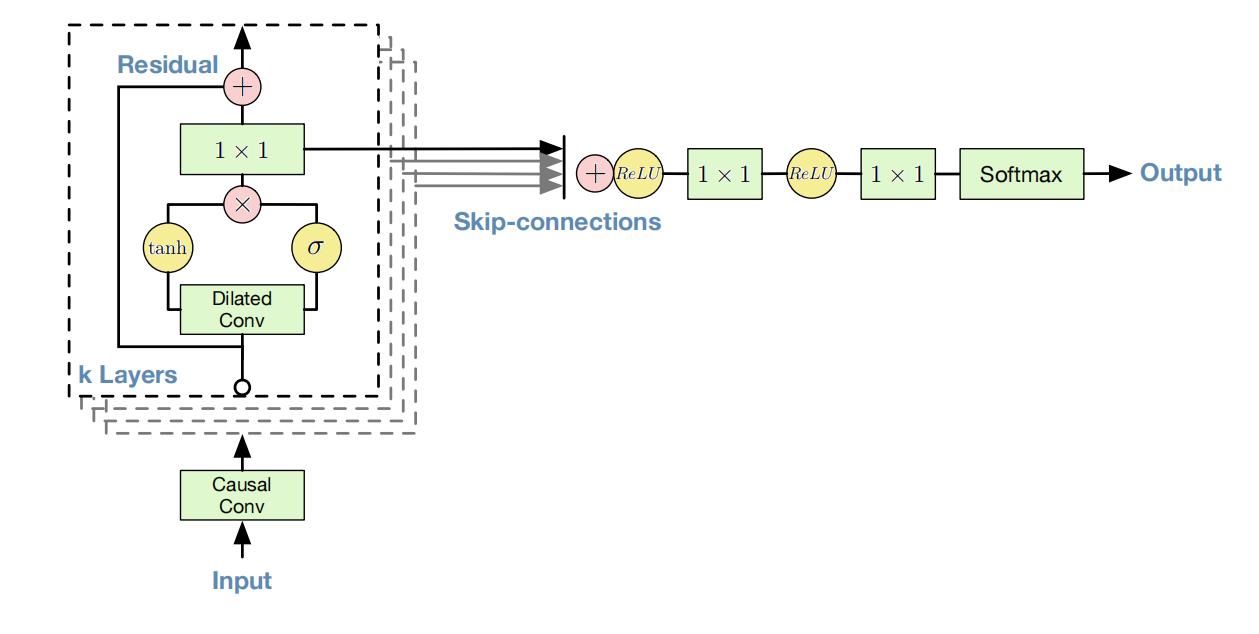
图 4 : 残 差 连 接 和 跳 过 连 接 \\color{green}{图4:残差连接和跳过连接} 图4:残差连接和跳过连接
残差连接和参数化跳过连接在整个网络中使用,保持网络稳定,以加快收敛速度,并能够训练更深入的模型。在图4中,展示了模型的残差块,它在网络中被多次堆叠。
条件生成
给定一个额外的输入
h
\\mathrm{h}
h, 可以模拟给定输入的音频的条件分布
p
(
x
∣
h
)
p(\\mathbf{x} \\mid \\mathbf{h})
p(x∣h)。Eq.(1)变成
p
(
x
∣
h
)
=
∏
t
=
1
T
p
(
x
t
∣
x
1
,
…
,
x
t
−
1
,
h
)
(3)
\\large \\color{green}{p(\\mathbf{x} \\mid \\mathbf{h})=\\prod_{t=1}^{T} p\\left(x_{t} \\mid x_{1}, \\ldots, x_{t-1}, \\mathbf{h}\\right)}\\tag{3}
p(x∣h)=t=1∏Tp(xt∣x1,…,xt−1,h)(3)
通过在模型上添加条件,引导网络生成具有所需特性的音频。例如,在多扬声器设置中,可以通过向模型提供扬声器标识作为额外输入来选择扬声器。类似地,对于TTS,提供关于文本的信息作为额外的输入。
以两种不同的方式对模型施加条件:全局条件作用和局部条件作用。全局条件反射的特征是一个单独的潜在表示
h
\\mathrm{h}
h,它影响所有时间步长的输出分布,例如,一个嵌入在TTS模型中的扬声器。Eq.(2)的激活函数现在为:
z
=
tanh
(
W
f
,
k
∗
x
+
V
f
,
k
T
h
)
⊙
σ
(
W
g
,
k
∗
x
+
V
g
,
k
T
h
)
(4)
\\large \\color{green}{\\mathbf{z}=\\tanh \\left(W_{f, k} * \\mathbf{x}+V_{f, k}^{T} \\mathbf{h}\\right) \\odot \\sigma\\left(W_{g, k} * \\mathbf{x}+V_{g, k}^{T} \\mathbf{h}\\right)}\\tag{4}
z=tanh(Wf,k∗x+Vf,kTh)⊙以上是关于2.4时序卷积网络TCN:因果膨胀卷积残差连接和跳过连接的主要内容,如果未能解决你的问题,请参考以下文章