环上的游戏

Posted 2020-11-09 adelalove

环上的游戏（cycle）
有一个取数的游戏。初始时，给出一个环，环上的每条边上都有一个非负整数。这些整数中至少有一个0。然后，将一枚硬币放在环上的一个节点上。两个玩家就是以这个放硬币的节点为起点开始这个游戏，两人轮流取数，取数的规则如下：
（1）选择硬币左边或者右边的一条边，并且边上的数非0；
（2）将这条边上的数减至任意一个非负整数(至少要有所减小)；
（3）将硬币移至边的另一端。
如果轮到一个玩家走，这时硬币左右两边的边上的数值都是0，那么这个玩家就输了。
如下图，描述的是Alice和Bob两人的对弈过程，其中黑色节点表示硬币所在节点。结果图(d)中，轮到Bob走时，硬币两边的边上都是0，所以Alcie获胜。

 

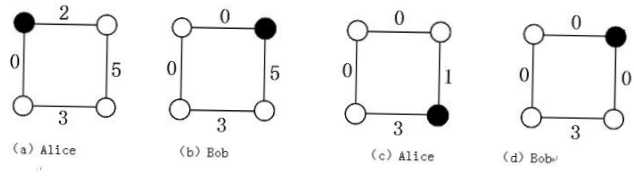
现在，你的任务就是根据给出的环、边上的数值以及起点（硬币所在位置），判断先走方是否有必胜的策略。
【输入格式】
第一行一个整数N（N≤20），表示环上的节点数。
第二行N个数，数值不超过30，依次表示N条边上的数值。硬币的起始位置在第一条边与最后一条边之间的节点上。
【输出格式】
仅一行。若存在必胜策略，则输出“YES”，否则输出“NO”。
【样例】
cycle1.in
4
2 5 3 0
cycle1.out
YES

cycle2.in
3
0 0 0
cycle2.out
NO

最后取到数的人获胜

解：首先根据题意分析可得假使走过一条边那么每次将它一点点减小到0

和一次性将它减小到0是一样的，那么不妨每走过一条边，就将边上的数值

减为0；

数据范围n<=20

那么我们可以搜索所有的可行路线，

（相当于剪枝）一旦存在先手赢的做法，就返回

 

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<algorithm>
 4 #include<cmath>
 5 #include<cstring>
 6 #include<string>
 7 using namespace std;
 8 int n,a[30];
 9 int L(int x)
10 {
11     int p=(x-1+n)%n;
12     if(p==0) p=n;
13     return p;
14 }
15 int R(int x)
16 {
17     int p=(x+1+n)%n;
18     if(p==0) p=n;
19     return p;
20 }
21 bool fg;
22 //1 Alice 2 Bob
23 void dfs(int nw,int peo)
24 {
25 //    cout<<"uu "<<nw<<" "<<peo<<endl;
26     if(fg) return;
27     if(a[nw]==0 && a[L(nw)]==0)
28     {
29        if(peo==2) fg=1; 
30        return;
31     }
32     if(a[nw])
33     {
34         int tmp=a[nw];a[nw]=0;
35         dfs(R(nw),3-peo);
36         a[nw]=tmp;
37     }
38     if(a[L(nw)])
39     {
40         int tmp=a[L(nw)];a[L(nw)]=0;
41         dfs(L(nw),3-peo);
42         a[L(nw)]=tmp;
43     }
44 }
45 int main()
46 {
47     freopen("cycle.in","r",stdin);
48     freopen("cycle.out","w",stdout);
49     scanf("%d",&n);
50     for(int i=1;i<=n;++i) scanf("%d",&a[i]);
51     dfs(1,1);
52 //    for(int i=1;i<=n;++i)
53 //     cout<<i<<" PPP "<<L(i)<<" "<<R(i)<<endl;
54     if(fg) printf("YES");
55     else printf("NO");
56     return 0;
57 }//数据范围小，搜索 

代码