NOIP200407合唱队形+最长上升子序列O(n^2)详解
Posted wxjor
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了NOIP200407合唱队形+最长上升子序列O(n^2)详解相关的知识,希望对你有一定的参考价值。
合唱队形解题报告
2016-05-12 4:30——6:45
|
NOIP200407合唱队形 |
|
难度级别:A; 运行时间限制:1000ms; 运行空间限制:256000KB; 代码长度限制:2000000B |
|
试题描述 |
|
N位同学站成一排,音乐老师要请其中的(N-K)位同学出列,使得剩下的K位同学排成合唱队形。 |
|
输入 |
|
第一行是一个整数N(2<=N<=100),表示同学的总数。第一行有n个整数,用空格分隔,第i个整数Ti(130<=Ti<=230)是第i位同学的身高(厘米)。 |
|
输出 |
|
包括一行,这一行只包含一个整数,就是最少需要几位同学出列。 |
|
输入示例 |
|
8 |
|
输出示例 |
|
4 |
|
其他说明 |
|
数据范围:n<=100。 |
代码:

1 #include<iostream> 2 3 using namespace std; 4 5 int b[110],c[110],a[110]; 6 7 // 分别定义了三个数组:数组a(用来储存输入数据),数组b(用来存储从a[1]到a[n]的最大严格上升子序列长度),数组c(用来存储从a[n]到a[1]的最大严格下降子序列长度) 8 9 int main() 10 11 { 12 13 14 15 int n,ans=0,i,j; 16 17 scanf("%d",&n);//输入 18 19 for(i=1;i<=n;i++) scanf("%d",&a[i]); 20 21 b[1]=1; 22 23 for(i=2;i<=n;i++) 24 25 //从a[2]开始求最大严格上升子序列长度 26 27 { 28 29 b[i]=1; 30 31 for(j=1;j<i;j++) 32 33 if(a[i]>a[j]) b[i]=max(b[i],b[j]+1); 34 35 //如果a[i]>a[j],则可能从a[1]到a[i]的最大严格上升子序列长度又增加了1。 36 37 } 38 39 c[n]=1; 40 41 //从a[n]开始求最大严格上升子序列长度 42 43 for(i=n-1;i>=1;i--) 44 45 { 46 47 c[i]=1; 48 49 for(j=n;j>i;j--) 50 51 if(a[i]>a[j]) c[i]=max(c[i],c[j]+1); 52 53 //如果a[i]<a[j],则可能从a[i]到a[n]的最大严格上升子序列长度又增加了1。 54 55 } 56 57 for(i=1;i<=n;i++) 58 59 if(b[i]+c[i]>ans) ans=b[i]+c[i];//更新答案 60 61 printf("%d",n-ans+1);//输出 62 63 }
《合唱队形》这道题其实就是《求最长下降/上升子序列》的翻版。但如果用循环直接搜固然很难办,而且不知道会用多长时间,所以,简单动态规划的思想很容易办到。
b[i]=1;
这句赋值语句固然很好理解,每一个元素,也可以视为一个符合题意的子序列,不论是最长上升、最长下降。所以从a[1]
到a[i]的符合题意的子序列必将有一个。比如有如下一组数。
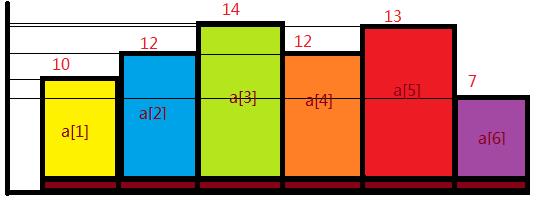
b[1]是 1,原因如上。
那b[2]呢?如图,它显然比a[1]高,在执行如下语句时
for(j=1;j<i;j++) if(a[i]>a[j])
j小于i,也就是2,目前符合条件的只有a[1],a[1]又通过了判断语句,它确实小于a[i],执行下一条语句:
b[i]=max(b[i],b[j]+1);
b[2]显然原来是1,当它和b[1]+1比时,1当然比2小,所以,b[2]自然就是2了。由此,这个方法只需要一维数组就行了。、

O(nlogn)的方法,将下次介绍。这样的方法的时间复杂度为O(n^2)。

b[1]=1;
解决完了这个问题,这道题就非常简单了,先从下往上搜一遍最长上升子序列,代码如下:
for(i=2;i<=n;i++)
{
b[i]=1;
for(j=1;j<i;j++)
if(a[i]>a[j]) b[i]=max(b[i],b[j]+1);
}
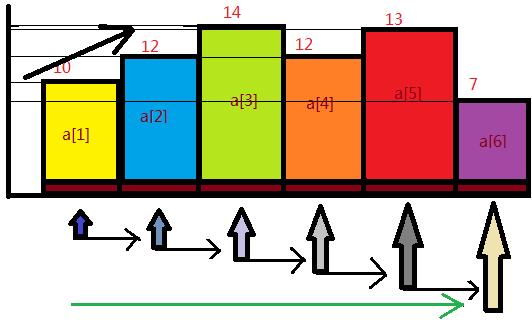
再反着从上往下搜一下最长上升子序列:
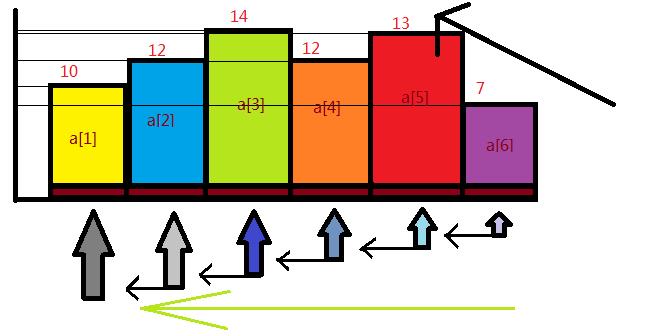
这段代码一定就很好理解了:
for(i=1;i<=n;i++)
if(b[i]+c[i]>ans) ans=b[i]+c[i];
一直更新ans,要求出队人数最少,自然要让保留人数最多。
最后输出n-ans+1。
以上是关于NOIP200407合唱队形+最长上升子序列O(n^2)详解的主要内容,如果未能解决你的问题,请参考以下文章
